Вычисление произведения матриц

Произведение матриц может быть вычислено, если количество столбцов умножаемой матрицы равно количеству строк матрицы множителя.

Если А = (а_ij) имеет размерность т x п, и В=(b_ij) с размерностью п р, то матрица С, полученная умножением матрицы А на матрицу В, будет иметь размер т р, а каждый ее элемент будет равен сумме произведений i-й строки матрицы А на соответствующие элементы j-ro столбца матрицы В:

Вычисление произведения матриц в табличном процессоре выполняется с помощью специальной функции рабочего листа, имя которой МУМНОЖ. Она имеет синтаксис:

МУМНОЖ(Массив1; Массив2),

где Массив1 - адрес диапазона, в котором записаны элементы первой матрицы;

Массив2 - адрес диапазона, в котором записаны элементы второй матрицы.

Пример 1.6 Умножить матрицу А= на матрицу В= . Решение в электронной таблице приведено на рис. 1.6.

Рис. 1.6

Решение систем линейных уравнений Метод обратной матрицы

Система т линейных уравнений с п неизвестными х_1, х₂,..., х_n имеет вид

Матрица А называется матрицей системы.

Свободные и неизвестные члены представляются в виде матриц-столбцов

В матричной форме система линейных уравнений записывается в виде А X=В.

В частном случае, когда число уравнений в системе (m) равно числу неизвестных (n), т.е. т = n, то решение такой системы можно найти и методом обратной матрицы в виде Х=А^-1 В - матрица, обратная по отношению к исходной матрице А.

Технологию решения системы линейных уравнений методом обратной матрицы рассмотрим на примере.

Пример 1.7 Система уравнений задана матрицами А= В= . Требуется решить заданную систему линейных уравнений.

Решение

Присвоим диапазону А3:В4 имя (например, А) и введем в ячейки значения элементов матрицы А.

Присвоим диапазону D3:D4 имя (например, В) и введем значения элементов вектора В.

Выделим область F3:F4 для помещения результата решения системы и введем в него формулу

=МУМНОЖ(МОБР(А);В).

Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter>, в ячейках диапазона F3:F4 будет получен результат (рис.1.7.).

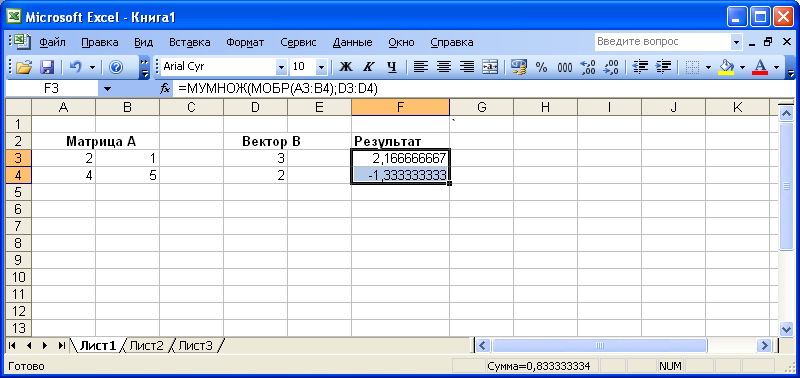
Рис. 1.7

Чтобы выполнить проверку полученных результатов, достаточно перемножить исходную матрицу на вектор результата, итогом этой операции является массив, содержащий такие же значения, как и вектор В.

При решении некоторых задач в электронной таблице в формулах удобно использовать ссылки на имена ячеек или диапазонов. Имя - это идентификатор. Область действия имени - вся рабочая книга. Для присвоения имени диапазону молено применить два приема:

• выделить диапазон и в поле имени записать идентификатор;

• выполнить команду меню Вставка/Имя/Присвоить. В открывшемся окне в поле Имя ввести идентификатор имени, а в поле Формула записать адрес диапазона (лучше в виде абсолютного адреса. Для установки абсолютного адреса используйте клавишу <F4c>.

Метод наименьших квадратов

Технология решения систем линейных уравнений для случая, когда т = п, рассмотрена выше. Однако в общем случае т может быть не всегда равно п. Возможны три случая: т < п, т = п. и т > п. При т < п, если система является совместной, то она не определена и имеет бесконечное множество решений.

В случае если т>п система совместна, то матрица А имеет по крайней мере т - п линейно независимых строк. В этом случае решение может быть получено отбором п любых линейно независимых уравнений и применением формулы х =А^-1 В. Однако при решении задачи в электронной таблице удобнее применить более общий подход - метод наименьших квадратов. Для этого обе части уравнения нужно умножить на транспонированную матрицу системы А^Т: А^Т АХ = А^TВ.

Затем обе части уравнения нужно умножить на (А^ТА)^-1 . Если эта матрица существует, то система определена. С учетом того, что (А^TА)^-1 А^ТА = Е, где Е - единичная матрица, решение системы будет иметь вид X = (А^ТА)^-1 А^ТВ.

Рассмотрим технологию решения систем линейных уравнений методом наименьших квадратов на примере.

Пример 1.8 Требуется решить систему уравнений:

Решение

Введем значения элементов матрицы А в диапазон ячеек рабочего листа (А2:В4).

Введем значения элементов вектора В в ячейки рабочего листа, например D2:D4.

Транспонируем исходную матрицу, для чего выделим диапазон ячеек размерность 3 2(А6:С7), введем в него формулу

=ТРАНСП(А2:В4).

Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> - в ячейках выделенного диапазона будут помещены элементы транспонированной матрицы.

Вычислим произведение А^TА, для чего выделим диапазон (А9:В10) и введем в него формулу

=МУМНОЖ(А6:С7;А2:В4).

Вычислим произведение А^ТВ, для чего выделим диапазон из двух ячеек (Е6:Е7) и введем в него формулу

=MУMHОЖ(A6:C7;D2:D4).

Выделим диапазон (D9:E10), введем в него формулу =МОБР(А9:В10) для вычисления обратной матрицы (А^тА)^-1. Матрица существует, следовательно, исходная система определена.

Для вычисления итогового результата - решения системы уравнений выделим диапазон (В12:В13) и введем в него формулу умножения матриц (А^ТА)^-1 А^ТВ

=МУМНОЖ(D9:Е10;А9:В10).

Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> - в ячейках диапазона В12:В13 будет получен результат решения системы (рис.1.8.).

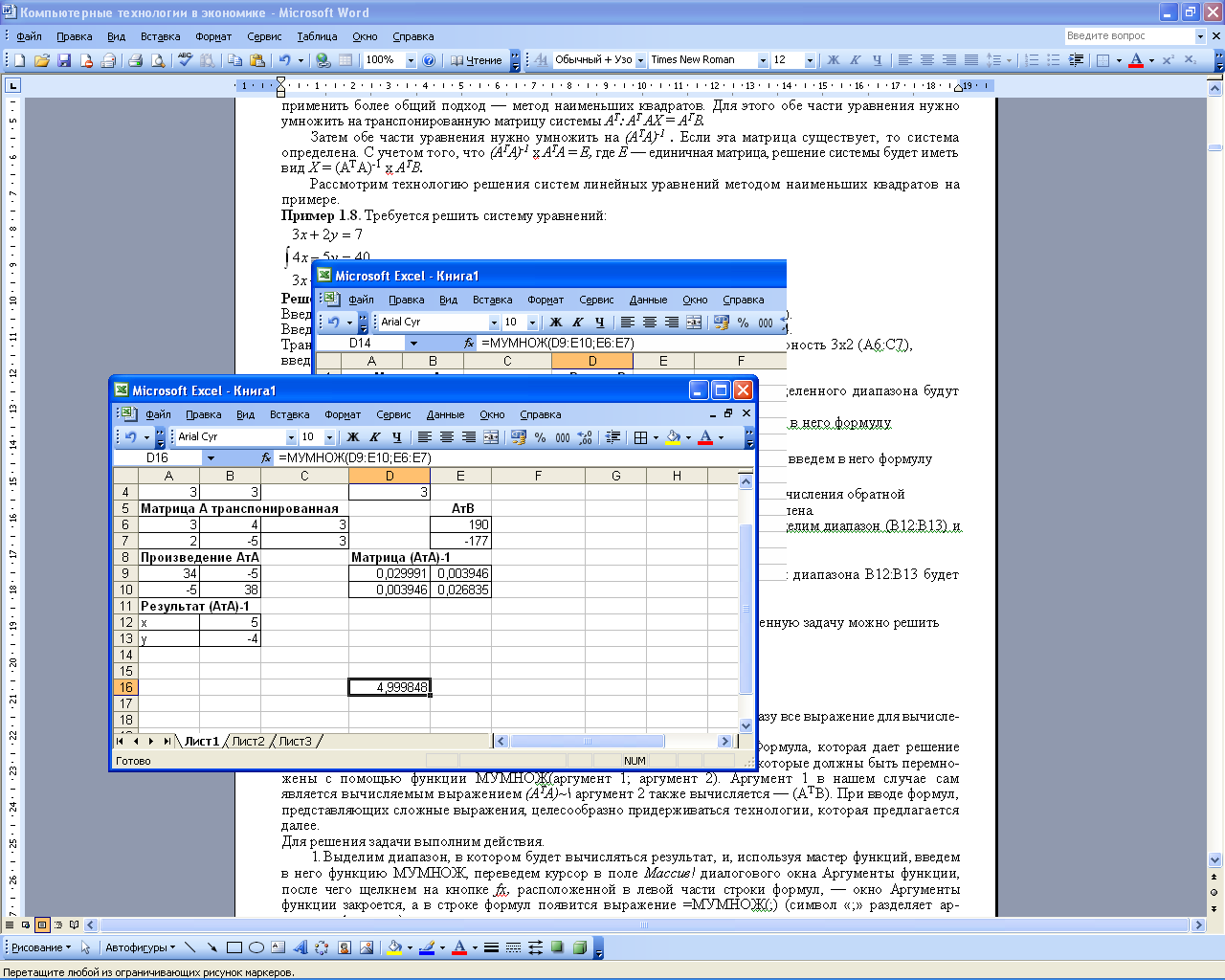
Рис. 1.8

При достаточно хорошем навыке работы с Мастером функций приведенную задачу можно решить без промежуточных вычислений, как это рассмотрено выше, а введя сразу все выражение для вычисления в строку формул.

Рассмотрим эту технологию более подробно на том же примере. Формула, которая дает решение системы X = (А^ТА)^-1 (А^ТВ) содержит две группы (заключенные в скобки), которые должны быть перемножены с помощью функции МУМНОЖ(аргумент 1; аргумент 2). Аргумент 1 в нашем случае сам является вычисляемым выражением (А^ТА)^-1, аргумент 2 также вычисляется - (А^ТВ). При вводе формул, представляющих сложные выражения, целесообразно придерживаться технологии, которая предлагается далее.

Для решения задачи выполним действия.

1. Выделим диапазон, в котором будет вычисляться результат, и, используя мастер функций, введем в него функцию МУМНОЖ, переведем курсор в поле Массив2 диалогового окна Аргументы функции, после чего щелкнем на кнопке fx, расположенной в левой части строки формул, - окно Аргументы функции закроется, а в строке формул появится выражение =МУМНОЖ(;) (символ «;» разделяет аргументы функции).

2. Первый аргумент в нашем случае является обратной матрицей результата произведения матриц. Переведем щелчком курсор в поле первого аргумента и, используя список Функции, включим функцию МОБР и закроем окно Аргументы функции, щелкнув на кнопке fx в левой части строки формул, При этом курсор остается в строке формул в поле аргумента функции МОБР.

3. Аргумент функции МОБР в рассматриваемой задаче является произведением матриц. Используя список Функции включим функцию МУМНОЖ. Переведем курсор в поле Массив2 диалогового окна Аргументы функции и укажем адрес массива, содержащего элементы матрицы А. Затем переведем курсор в поле Массив2 диалогового окна и, используя список Функции, включим функцию ТРАНСП и в качестве ее аргумента укажем адрес массива, содержащего элементы матрицы А. Щелкнем на кнопке fx - окно Аргументы функции закроется.

4. В строке формул установим курсор в область второго аргумента первой функции МУМНОЖ. Используя список Функции, включим функцию МУМНОЖ. Поскольку второй аргумент не нужно вычислять, в первую очередь укажем его: в поле Массив2 введем адрес диапазона, в котором содержатся элементы вектора В.

5. Переключим курсор в поле Массив2 диалогового окна Аргументы функции, используя список Функции, включим функцию ТРАНСП и в поле Массив этой функции укажем адрес диапазона, в котором содержатся значения элементов матрицы А. Запись формулы для решения системы уравнений методом наименьших квадратов завершена. Она имеет окончательный вид

=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(А2:В4);А2:В4)); МУМНОЖ(ТРАНСП(А2:В4);D2:D4)).

6. Нажмем комбинацию <Ctrl>+<Shift>+<Enter> - в ячейках выделенного диапазона будет результат решения системы (рис. 1.9).

Рис. 1.9 Пример решения системы линейных уравнений

На первый взгляд приведенная процедура может показаться сложной и длительной. Однако это кажется только на первый взгляд. При достаточном ее освоении значительно сокращается время решения и уменьшается вероятность ошибки.