Технологии решения задач корреляционного анализа
Одной из задач статистического моделирования является изучение связи между некоторыми наблюдаемыми переменными. Результаты, полученные при таком исследовании, позволяют прогнозировать - развитие ситуации в случае изменения конкретных характеристик изучаемого объекта или процесса. Задача подобного исследования решается методами корреляционного анализа.
Под корреляцией понимается взаимосвязь некоторых величин, представленных данными - векторами или матрицами. Общепринятой мерой линейной корреляции является коэффициент корреляции. Его близость к единице указывает на высокую степень линейной зависимости. Целью решения задачи является получение корреляционной матрицы, которая представляет собой симметричную матрицу с единичной диагональю.
В табличном процессоре для целей корреляционного анализа служит инструмент Корреляция, который позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами. Корреляционная матрица - это квадратная таблица, на пересечении соответствующих строк и столбцов которой располагаются корреляционные коэффициенты.
Для выполнения корреляционного анализа необходимо выполнить следующую последовательность операций.
1. Выполнить команду меню Сервис/Анализ данных.
В списке Инструменты анализа диалогового окна Анализ данных выбрать строку Корреляция.
В раскрывшемся окне диалога Корреляция в поле Входной интервал ввести адресную ссылку на диапазон, содержащий анализируемые данные (входной интервал должен состоять не менее чем из двух столбцов), установить соответствующий переключатель Группировка, установить переключатель Параметры вывода и ввести адрес верхней левой ячейки, с которой будет начинаться диапазон для вывода результатов вычислений.
4. Щелкнуть на кнопке ОК.
В результате выполнения вычислений в выходной диапазон будет помещена корреляционная, матрица.
Пример 2.16 Есть статистические данные, регистрирующие количество выходных и праздничных дней в месяце в период с января по июнь и снимаемые со счетов суммы (таблица 2.7).
Данные наблюдений
Таблица 2.7
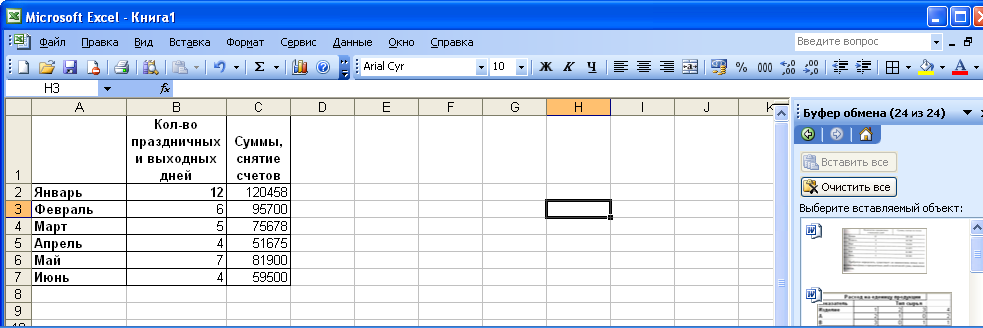
Требуется определить, существует ли взаимосвязь между количеством выходных и праздничных дней и величиной сумм, снимаемых со счетов.
Решение
Введем в диапазон рабочего листа (А1:С8) данные приведенной таблицы.
Выполним команду меню Сервис/Анализ данных.
В раскрывшемся окне диалога Анализ данных из списка выберем Корреляция.
В окне диалога Корреляция (рис.2.22):
в группе Входные данные в поле Входной интервал укажем адресную ссылку на диапазон, содержащий исходную таблицу (В2:С8), установим переключатель Группирование по столбцам и установим флажок Метки в первой строке;
в группе Параметры вывода установим переключатель Выходной интервал и введем адресную ссылку на ячейку, которая будет началом диапазона выходного интервала (Е2).
Щелкнем на ОК (таблица 2.8)
Таблица 2.8
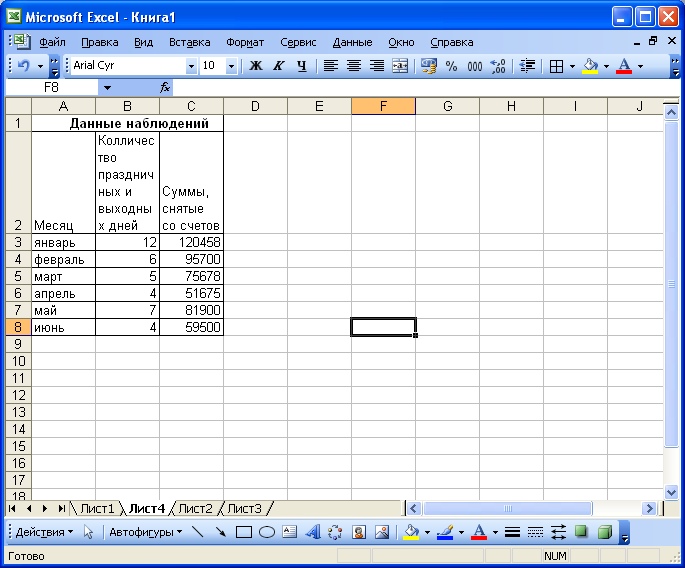
Рис. 2.22
После выполнения вычислений в диапазон E2:G4 будет выведена результирующая корреляционная матрица (рис. 2.23).
Рис. 2.23
Корреляционная матрица является треугольной с единичной диагональю. На самом деле она должна рассматриваться как симметричная, т.е. rij=rij.
Из анализа полученной корреляционной матрицы видно, что коффициент корреляции между количеством выходных дней и величиной суммы, снимаемой со счетов r = 0,91668. Таким образом, существует сильная прямая линейная связь между количеством выходных N праздничных дней и величинами сумм, снимаемых со счетов.