Вычисление доверительного интервала для среднего значения

Для вычисления доверительного интервала в MS Excel можно использовать специальную функцию ДОВЕРИТ или инструмент Описательная статистика.

Функция ДОВЕРИТ (альфа; станд_откл; размер) вычисляет ширину доверительного интервала. Ее параметрами являются:

• альфа - уровень значимости, используемый для вычисления доверительной вероятности;

• станд_откл - стандартное отклонение генеральной совокупности для интервала данных (предполагается известным или предварительно вычисляется);

• размер - размер выборки.

Пример 2.12 Требуется найти границы 90% интервала для среднего значения, если по результатам 24 торгов среднее значение стоимости доллара составило 28 руб., а стандартное отклонение - 35 коп.

Решение

1. Установим курсор в любую свободную ячейку рабочего листа и установим для нее денежный формат.

2. Выполним команду меню Вставка/Функция. В окне Мастер функций в категории Статистические выберем из списка функцию ДОВЕРИТ.

3. В поля аргументов окна ДОВЕРИТ введем исходные данные: альфа - 0,1; станд_откл - 0,35; размер - 24.

После щелчка на ОК в ячейке будет вычислена полуширина 90% доверительного интервала для среднего значения выборки - 0,12 руб.

Таким образом, с 90%-ным уровнем надежности можно утверждать, что средняя стоимость доллара в диапазоне 27 руб. 88 коп. – 28 руб. 12 коп (рис. 2.16).

Рис. 2.16

Пример 2.13 Дана выборка стоимости валюты: 27,70; 27,85; 28,12; 28,20; 28,10; 27,75; 28,25 (рублей). Необходимо определить границы 95% доверительного интервала для среднего.

Решение

1. Введем в диапазон ячеек А2:А8 заданный массив чисел.

2. Включим инструмент Описательная статистика.

3. В поле Входной интервал диалогового окна Описательная статистика укажем ссылку на диапазон, содержащий выборку (А1:А8). Включим переключатель Выходной диапазон и в соответствующем поле укажем ссылку на ячейку, где будет размещен верхний левый угол результирующей таблицы (В2). Установим флажок Уровень надежности и в соответствующем поле введем число 95%. Установим флажок Метки в первой строке.

4. Щелкнем на ОК - на рабочий лист в указанный диапазон будет выведен результат (рис. 2.17).

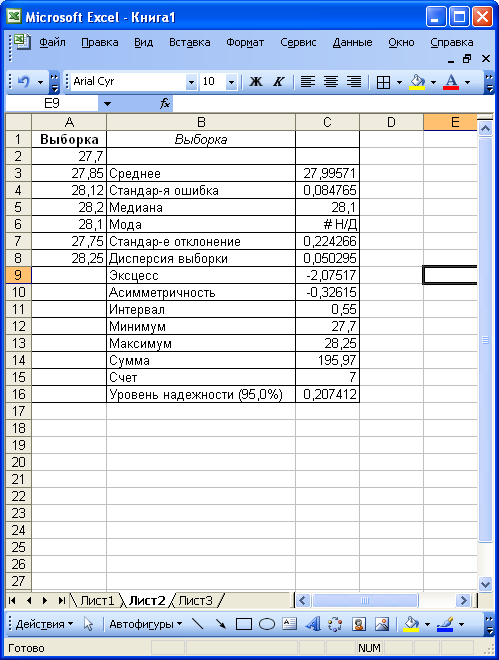
Рис. 2.17

В результате вычислений для доверительной вероятности 0,95 и графе Уровень надежности получим величину доверительного интервала 0,207412. Это означает, что с вероятностью 0,95 для заданной Генеральной совокупности среднее значение будет находиться в интервале 27,99571 +/- 0,207412 (нижняя граница доверительного интервала 27,7883, верхняя граница - 28,20312).

Технология проверки соответствия данных, полученных экспериментально, теоретическому распределению

При решении практических задач закон распределения случайных величин и его параметры неизвестны. Однако для решения задачи необходимо иметь информацию о том, каков закон распределения и каковы его параметры. В этом случае решают задачу проверки гипотезы. Исходя из предположения (гипотезы), что распределение случайных чисел подчиняется тому или иному закону, выполняют проверку этой гипотезы. Суть задачи проверки соответствия сводится к оценке меры соответствия экспериментальных данных и какого-либо теоретического распределения. Методом проверки соответствия теоретическому распределению является использование критерия согласия. Одним из них является критерий согласия хи-квадрат.

В табличном процессоре проверка согласия по критерию хи-квадрат реализуется функцией ХИ2ТЕСТ. Эта функция вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости ( < 0,05), то утверждается, что экспериментальные значения не соответствуют теоретическому распределению.

Функция имеет параметры:

ХИ2ТЕСТ(фактический интервал; ожидаемый интервал);

где фактический интервал - диапазон данных, который содержит результаты наблюдения, подлежащие сравнению с ожидаемыми значениями;

ожидаемый интервал - диапазон данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Для получения правильных результатов необходимо, чтобы объем выборки был не менее 40, выборочные данные сгруппированы в интервальный ряд с количеством интервалов не менее 7, а количество наблюдений в каждом интервале (частот) не менее 5.

Пример 2.14 Требуется проверить соответствие нормальному закону распределения выборочных данных результатов сдачи экзамена, оцененных в следующих баллах: 48, 51, 67, 70, 64, 71, 85, 79, 80, 83, 86, 01,99, 56, 66, 65, 84,84,84, 75, 76, 77, 78, 80, 86, 88, 58, 69, 65, 81, 75, 78, Ь 80, 80, 83, 86, 80, 89, 60, 68, 55, 82, 64, 71, 72, 72, 73, 74, 74, 79.

Решение

1. В диапазон ячеек рабочего листа введем исходные данные в виде таблицы, содержащей баллы из приведенной выборки.

2. Выберем ширину интервала, равную 5 баллам, начиная от 50 до 100, и введем в диапазон F2.F12 граничные значения интервалов.

3. Подготовим заголовки создаваемой таблицы (ячейки G1, H1, I1).

4. Применяя функцию ЧАСТОТА, рассчитаем абсолютные час­тоты попаданий случайных величин в установленные интервалы - столбец Абсолютные частоты.

5. В ячейке Н15 вычислим общее количество наблюдений, используя формулу =CУMM(G2:GH) (рис.2.18).

Рис. 2.18

6. В ячейке Н16 вычислим среднее значение выборки, а в ячейке Н17 - стандартное отклонение.

7. Вычислим теоретические частости распределения. Поскольку мы проверяем соответствие заданной совокупности случайных величин нормальному закону распределения, то для расчета применим функцию НОРМРАСП. Установим курсор в ячейку Н2 и вызовем из Мастера функций функцию НОРМРАСП. Заполним поля аргументов: х - F2, среднее - $Н$16, стандартное_откл. - $Н$17, интегральный - 0, щелкнем на ОК.

8. В ячейку НЗ введем формулу =НОРМРАСП(F3;$Н$16; $Н$17;1)-СУММ($Н$2:Н2).

9. Скопируем введенную формулу в ячейки диапазона Н4:Н12.

Для вычисления теоретических частот установим курсор в ячейку 12 и введем формулу = $Н$16* Н2. Скопируем содержимое этой ячейки в ячейки диапазона I3:I12 (рис. 2.19).

Применяя функцию ХИ2ТЕСТ, определим соответствие данных выборки нормальному закону распределения. Для этого:

• установим курсор в свободную ячейку 114, включим Мастер функций, выберем категорию Статистические, а в списке функций - функцию ХИ2ТЕСТ;

• заполним поля аргументов функции: фактический - введем адрес диапазона абсолютных частот G2:G12, ожидаемый - адрес диапазона теоретических частот I2:I12. После щелчка на кнопке ОК в ячейке I14 будет вычислено значений вероятности того, что выборочные данные соответствуют нормальному закону распределения - 0,917143314.

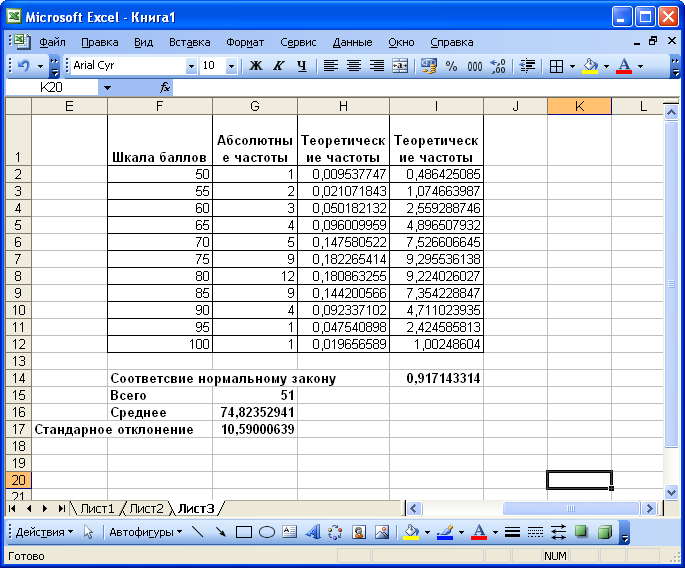
Рис. 2.19

Поскольку полученная вероятность соответствия экспериментальных данных р = 0,917143314 намного больше уровня значимости =0,05, то можно утверждать, нулевая гипотеза не может быть отвергнута и экспериментальные данные не противоречат нормальному закону распределения. Но так как полученное значение вероятности очень мало отличается от 1, то можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормальному закону.