Нормальный закон распределения
В табличном процессоре для вычисления значений нормального распределения есть специальные функции: НОРМРАСП, НОРМСТРАСП, НОРМОБР, НОРМСТОБР и НОРМАЛИЗАЦИЯ.
Функция НОРМРАСП вычисляет значения вероятности нормальной функции распределения для заданного среднего и стандартного отклонения. Она имеет параметры:
НОРМРАСП(х; среднее; стандартное_откл; интегральная),
где х - значение, для которого строится распределение;
среднее - среднее арифметическое распределения;
стандартное_откл - стандартное отклонение распределения;
интегральная - логическое значение, определяющее форму функции. Если параметр интегральная имеет значение ИСТИНА (1), то функция возвращает интегральную функцию распределения, в противном случае возвращает значение функции плотности распределения. Если параметры среднее = 0 и стандартное_откл = 1, то функция вычисляет стандартное нормальное распределение.
Для вычисления стандартного нормального интегрального распределения в библиотеке табличного процессора есть специальная функция НОРМСТРАСП. Она имеет параметры
НОРМСТРАСП(z), где z - значение случайной величины, для которого вычисляется распределение.
Функция НОРМОБР служит для вычисления квантилей для указанного среднего и стандартного отклонения (решается уравнение F(x) - p).
Функция имеет параметры
НОРМОБР(вероятность; среднее; стандартное_откл), где вероятность - вероятность, соответствующая нормальному распределению;
среднее - среднее арифметическое распределения;
стандартное _откл - стандартное отклонение распределения.
Функция НОРМСТОБР предназначена для вычисления квантилей стандартного нормального распределения, единственным ее параметром является величина вероятности.
Функция НОРМАЛИЗАЦИЯ по заданному значению х и параметрам распределения вычисляет нормализованное значение, соответствующее х.
Рассмотрим технологию применения приведенных функций на примерах.
Пример 2.8
Требуется построить диаграмму нормальной
функции плотности вероятности f(х)
при М= 24,3 и
= 1,5.
Решение
В ячейку A3 введем символ х, а в ячейку ВЗ - символ функции плотности вероятности f(x).
Вычислим нижнюю М - За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =24,3-3*1,5, а также верхнюю границу - в ячейку Е2 введем формулу =24,3+3*1,5.
Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.
Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.
В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение - число, равное верхней границе диапазона.
Щелкнем на кнопке ОК. В диапазоне А4:А22 будет сформирована последовательность значений х.
Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций - НОРМРАСП.
Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее - введем число 24,3, для параметра Стандартное_откл - число 1,5, для параметра Интегральное - число 0 (весовая) (рис.2.9).
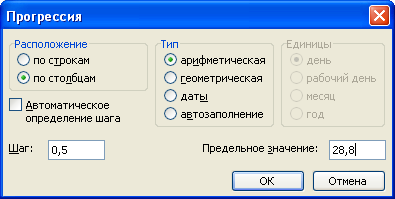
Рис. 2.9
Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В22.
Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В22) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид - вид графика, щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А22). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности (рис. 2.10).
Рис. 2.10