Технология численного вычисления определенного интеграла

Интегральное исчисление в экономике применяется для решения таких задач, как, например, вычисление издержек по заданной функции предельных издержек, для нахождения дисконтированной стоимости денежного потока и др.

Для численного вычисления определенного интеграла с использованием конечных разностей существует несколько методов. Наиболее простым является метод трапеций, для которого справедлива формула

Как можно заметить, абсолютная погрешность вычисленного значения зависит от величины задаваемого конечного приращения аргумента х. Чем меньше это значение, тем точнее результат.

При вычислении величины определенного интеграла в табличном процессоре можно использовать две технологии: приближенного вычисления и точного вычисления.

Технология приближенного вычисления

Технология приближенного вычисления определенного интеграла в табличном процессоре основана на построении табличных значений подынтегрального выражения для каждого из значений аргумента функции, задаваемых на отрезке, определяемом пределами интегрирования с достаточно малым шагом. Используя его, можно получить лишь приближенное значение интеграла.

Технологию приближенного вычисления определенного интеграла в табличном процессоре с использованием формулы трапеций рассмотрим на примере.

Пример 1.29

Требуется вычислить определенный интеграл .

Величина интеграла, вычисленная аналитически, равна 9.

Решение

Табулируем подинтегральную функцию в диапазоне изменения значений аргумента 0-3 с шагом 0,2.

В ячейку С2 введем формулу =(А3-А2)*В2+(А3-А2)*(В3-В2)/2, которая реализует часть размещенной правее знака суммы приведенной выше формулы трапеций, т.е. вычисляет величину элементарной площадки (криволинейной трапеции).

Скопируем буксировкой формулу, записанную в ячейке С2, до значения аргументах х= 2,8. В ячейке С17 просуммируем с помощью автосуммирования полученные результаты. Вычисленное значение в ячейке С17 и будет величиной интеграла – 9 (рис. 1.37).

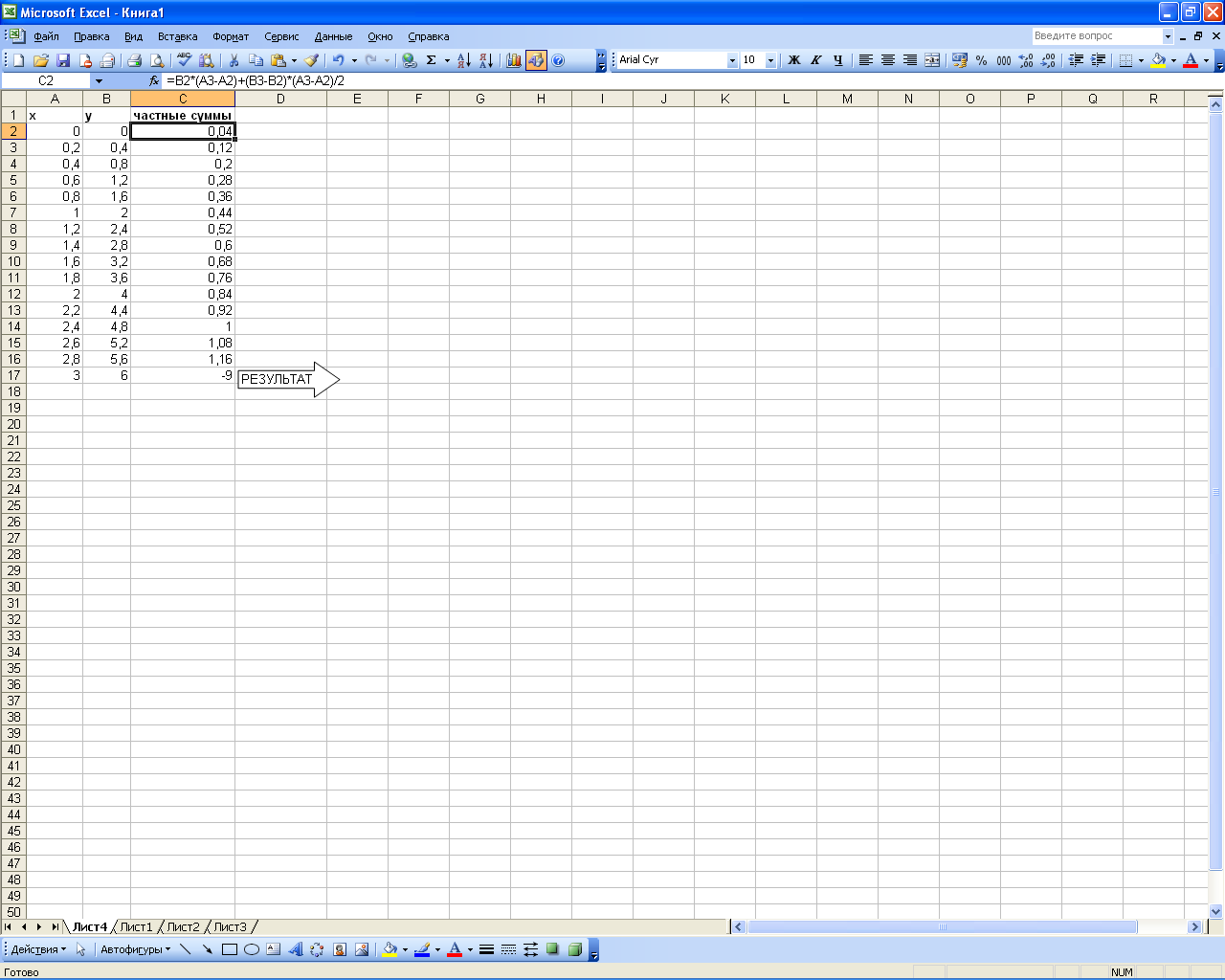
Рис. 1.37

Технология точного вычисления

Технология точного вычисления основана на использовании аппарата циклических ссылок и итераций табличного процессора. Применение этой технологии позволяет задавать достаточно малый шаг интегрирования, что увеличивает точность вычислений. Для точного вычисления выполним следующие операции:

-определим, на сколько интервалов нужно разбить диапазон интегрирования, чтобы получить требуемую точность, и задать их количество в виде числа итераций. Положим для решения нашей задачи достаточно 10000 интервалов;

- выполним команду меню Сервис/Параметры, откроем закладку Вычисления в диалоговом окне Параметры и в поле Предельное число итераций введем число 10 000. Если установлен флажок Итерации, то выключим его. Закроем диалоговое окно Параметры;

-в ячейки рабочего листа введем исходные данные и формулы для вычислений (рис. 1.38).

Рис. 1.38 Пример реализации технологии точного вычисления определенного интеграла

В ячейке В6 формула =(В4-В2)/В5 вычисляет шаг интегрирования. В ячейке С3 формула =0+С3+В6 - вычисляет текущее значение аргумента х. Значение 0 в формуле устанавливает нижний предел интегрирования. В формуле есть циклическая ссылка на эту же ячейку С3+В6, она реализует накопление величины х относительно нижнего предела интегрирования.

В ячейке D3 записана формула, реализующая метод трапеций и накопление суммы площадей элементарных трапеций.

После ввода исходных данных и формул вновь выполним команду меню Сервис/Параметры, откроем закладку Вычисления в диалоговом окне Параметры и установим флажок Итерации. Щелкнем на кнопке ОК. Потребуется некоторое время для того, чтобы табличный процессор выполнил заданное количество циклов итераций и вычислил результат.

После завершения вычислений вновь вызовем диалоговое окно Параметры и выключим флажок Предельное число итераций.