Вычисление предельных экономических показателей

В экономических задачах одни экономические показатели являются функциями каких-либо других показателей или величин. Иначе существует зависимость одних показателей от других: у =f(x).

Так, например, себестоимость продукции зависит от производимого объема С =f(Q), издержки производства зависят от количества выпускаемой продукции, величина созданного общественного продукта зависит от совокупных затрат живого труда и суммарного объема применяемых производственных фондов и т.п.

Предельные экономические показатели характеризуют величину прироста величины функции Δу от прироста ее аргумента Δх.

ПY=Δy:Δx.

Так, например, предельная себестоимость характеризует себестоимость ΔС прироста продукции ΔQ:

ПY=ΔC:ΔQ.

Если зависимость Δy от Δх непрерывна, то приведенное разностное уравнение можно заменить производной ПY=f^’(x).

Пример 1.27

Зависимость издержек производства от объема выпускаемой продукции в денежных единицах выражается формулой C = 20Q-0,05Q³.

Требуется определить предельные издержки производства при объеме выпускаемой продукции 10 ден. ед.

Решение

Предполагая, что в ячейке А2 рабочего листа будет записано значение Q_k - левая граница окрестности точки Q = 10, в ячейку В2 введем формулу

=20*А2-0,05*А2^{^}3.

Скопируем введенную формулу в ячейку В3.

В ячейку С3 введем формулу вычисления производной =(В3-В2)/(А3-А2).

В ячейки А2 и A3 введем значения Q для левой и правой окрестности точки Q = 10 (рис.1.34).

Рис. 1.34

После выполнения приведенных выше операций в ячейке С2 будет получен результат, отображенный на рис.1.35.

Рис. 1.35

Таким образом, предельные издержки производства при объеме выпускаемой продукции 10 ден. ед. составляют примерно 4,99999 ден. ед.

Вычисление эластичности экономических показателей

Под эластичностью экономического показателя понимается процентное изменение величины значения величины функции, определяющей зависимость одного показателя от другого, при изменении ее аргумента на 1%. Так, например, при анализе и прогнозах ценовой политики применяется понятие эластичности спроса.

Пусть у = f(x) - функциональная зависимость показателя у от другого - х. Тогда эластичность у определится выражением

При достаточно малых значениях эластичность можно определить как

Рассмотрим технологию вычисления эластичности экономических показателей на примере.

Пример 1.28

Спрос на товар определяется функциональной зависимостью D(P) = 100 - 3Р.

Требуется определить эластичность спроса при цене на товар Р=20 ден. ед.

Решение

Конечно, в приведенной задаче функция спроса от цены задана простым выражением и эластичность можно вычислить аналитически, но мы, чтобы продемонстрировать технологию, решим задачу в электронной таблице. Выполним следующие действия.

В рабочие ячейки A3 и А4 введем границы окрестности точки Р=20.

В ячейки В3 и В4 введем формулы, вычисляющие значения функции.

В ячейку С3 введем формулу для вычисления производной функции.

В ячейку D3 введем формулу, вычисляющую эластичность (рис.1.36).

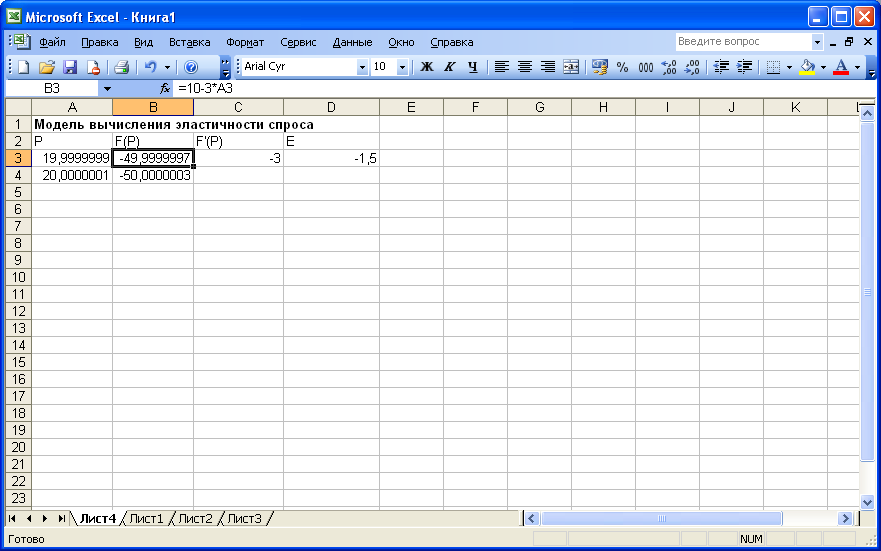
Рис. 1.36