Применение технологии исследования функций для решения экономических задач Кривые спроса и предложения, точка равновесия

Рассмотренные технологии исследования функций полезны для решения некоторых экономических задач. Одной из таких задач являются и определение точки равновесия спроса и предложения. Известно, что чем ниже цена (р), тем больше спрос (D) при постоянной способности населения. Обычно зависимость спроса и цены в графическом представлении имеет вид ниспадающей линии чаще всего приближающейся к прямой. В свою очередь предложение растет с увеличением цены на товар и в графическом представлении имеет вид восходящей линии.

Если зависимость спроса от цены определяется функцией D=f(p), а зависимость предложения от цены S = (р), то условие равновесия определяется уравнением

, где

U соответствует точке пересечения кривых D и S. Цена Р₀, при которой выполняется условие, называется равновесной.

Рассмотрим технологию решения задачи по определению точки равновесия на примере.

Пример 1.25 Зависимость спроса у на некоторый товар от цены х выражается уравнением , а зависимость предложения от цены – уравнение f₂(x)=x²-y+1. Требуется решить систему уравнений найти точку равновесия в диапазоне с точностью 0,001.

Решение

Приведем исходные уравнения к системе следующего вида

Создадим последовательность значений с х с шагом 0,2.

Рассчитаем значения функций спроса f(x) и предложения для сформированной последовательности значения х.

Подведем указатель мыши к точке пересечения кривых – отобразится приближенные координаты точки равновесия. В данном случае цена х в точке равновесия равна 1,6, предложение и спрос характеризуется величиной (рис. 1.30).

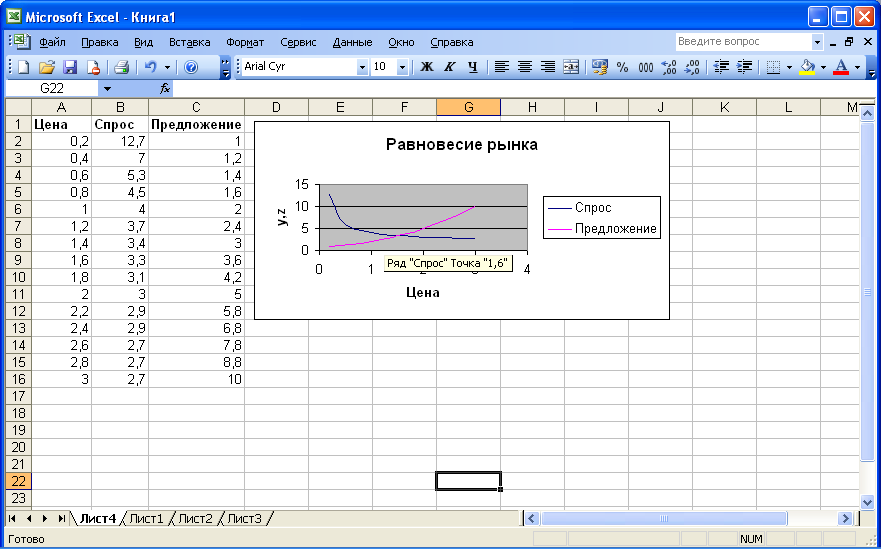
Рис. 1.30

Применяя приведенную раньше технологию, уточним решение. Результат уточнения приведен на рис.1.31.

Рис. 1.31

Таким образом, равновесное значение цены составляет 1,521, а спрос и предложение находятся в равновесии и выражаются величиной

Технология построения и исследования паутинной модели рынка

Известно, что процесс достижения равновесной цены является динамическим и представляет собой форму торга, при котором продавец назначает свою цену Р₁. Покупатель оценивает спрос D₁ при этой цене и определяет свою цену Р₂, при которой этот спрос D₁ равен предложению. Цена Р₂ ниже равновесной, так как покупатель стремится купить дешевле. В свою очередь продавец оценивает спрос D₂, соответствующей по цене Р₂ и назначает свою цену Р₃, эта цена выше равновесной – продавец стремится продать дороже.

Этот процесс торга продолжается и при определенных условиях приближается к устойчивому приближению к равновесной цене. Этот процесс графически можно изобразить в виде спирали, которая, в зависимости от условий, может быть скручивающейся, и тогда компромиссная цена приближается к равновесной, раскручивающейся – в этом случае компромисс не будет найден, или спираль имеет замкнутую форму – в этом случае продавец и покупатель остается каждый со своей равновесной ценой.

Приведенный процесс иллюстрируется на рис. 1.32.

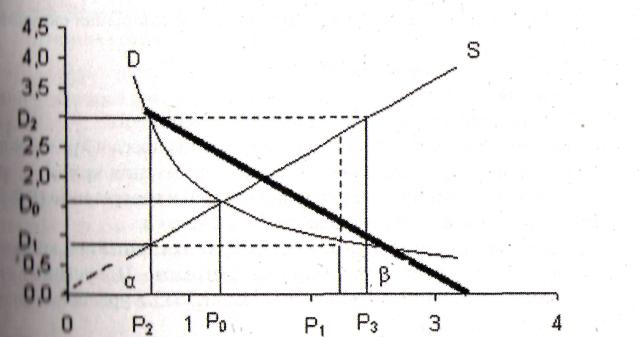
Рис. 1.32 Графическое изображение паутинной модели рынка

На приведенном рисунке процесс имеет вид раскручивающейся спирали. Из рисунка нетрудно заметить, что вид спирали зависит от соотношения величин углов наклона а и сглаживающих прямых в пределах границ разумно допустимых цен. При а = спираль имеет замкнутую форму, при а> - спираль скручивается, в противном случае - спираль раскручивается. Величины углов наклона линий тренда определяются величинами коэффициентов а и . Таким образом, задача определения вида процесса состоит в вычислении величин этих коэффициентов и последующего сравнения.

Пример 1.26

Торговая фирма по результатам реализации одного из видов товаров в течение нескольких периодов времени получила следующие экспериментальные данные (табл. 1.7):

Таблица 1.7

№ периода	Цена (усл. ед.)	Спрос	Предложение
1	0,0	3,0	2,0
2	0,2	2,8	2,5
3	0,3	2,4	3,5
4	0,4	2,1	3,9
5	0,5	2,0	4,7
6	0,6	1,7	5,2

Требуется:

1. Определить является ли паутинная модель рынка скручивающейся.

2. Найти равновесную цену.

Решение

Введем данные таблицы в ячейки рабочего листа.

По табличным данным построим графики спроса и предложения, подведем указатель мыши к точке пересечения кривых спроса и предложения - отобразятся координаты точки пересечения (0,2; 2,8). Таким образом, равновесная цена равна 0,2 усл. ед.

Построим линии тренда для обеих кривых с линейной аппроксимацией и отображением уравнения на диаграмме. Полученное ypaвнение предложения имеет вид у = 6,5714Х+ 1,3333, а уравнение спроса у = -2,6286х + 3,2533.

Величина коэффициента α= 2,6286, а коэффициента β = 6,5714, т.е. β > α. Следовательно, модель паутинного рынка раскручивается (рис.1.33).

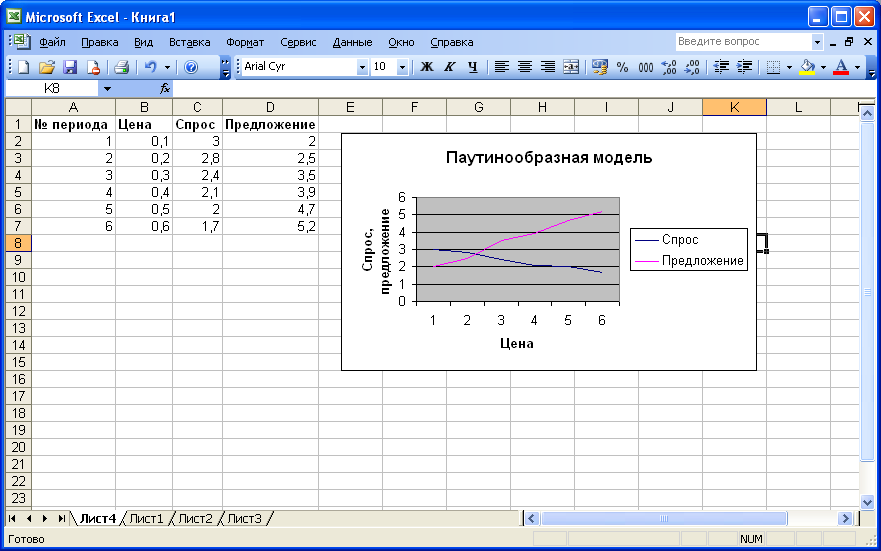
Рис. 1.33