Технология получения математической модели функции по ее табличному представлению
На практике часто бывает необходимо получить аналитическую формулу для функциональной зависимости, полученной экспериментально, модель которой представлена в виде таблицы. Это бывает необходимо в тех случаях, когда нужно найти значение функции в тех точках внутри данного интервала, где она таблично не задана - задача Интерполяции, либо вычислить значение функции в точках за пределами заданного интервала - задача экстраполяции.
Решение задач интерполяции и экстраполяции обеспечивается построением интерполяционной или аппроксимирующей функции L(x), приближенно заменяющей исходную f(x), заданную таблично. Подбор аналитической формулы сводится к вычислению входящих в нее параметров таким образом, чтобы из всех функций такого вида выбрать ту, которая наилучшим образом описывает зависимость между изучаемыми величинами.
При построении аппроксимирующей функции должны быть решены следующие вопросы:
- выбор типа аппроксимирующей функции L(x);
- оценка погрешности аппроксимации.
Подбираемая эмпирическая функция в зависимости от характерны экспериментальных данных может быть следующих видов:
- линейная (у = ах + b) обычно применяется в тех случаях, когда экспериментальные данные изменяются относительно постоянно;
- полиноминальная (у = а0 + а1х +а2 х2+ ...+ an хn) - используется для описания экспериментальных данных, попеременно возрастающих и убывающих;
- логарифмическая (у = а lпх + b), где а и b - константы, - применяется для описания экспериментальных данных, которые первоначально быстро возрастают или убывают, а затем постепенно стабилизируются;
- степенная (у = bx-a ), где a u b - константы, - используется для аппроксимации экспериментальных данных, скорость изменения которых увеличивается или уменьшается;
- экспоненциальная (y=beax), где а и b - константы, - применяется экспериментальных данных, которые быстро возрастают или убывают, а затем стабилизируются.
Близость исходной и аппроксимирующей функций определяется критерием аппроксимации. Наиболее распространен квадратичный критерий (R2), именно такой критерий оценки применяется в табличном процессоре. Не вдаваясь в подробности вычисления этого критерия, скажем: чем ближе значение этого критерия к единице, тем ближе аппроксимирующая функция к исходной, тем точнее полученная аналитическая модель отражает функциональную зависимость.
Чтобы получить аппроксимирующую формулу в табличном процессоре, нужно выполнить следующую последовательность действий:
- построить по имеющейся таблице экспериментальных данных графическую модель функции;
- установить указатель мыши на линию графика (ряд) и вызвать контекстное меню;
- в контекстном меню выбрать Добавить линию тренда - откроется диалоговое окно Линия тренда;
- в диалоговом окне Линия тренда на вкладке Тип, учитывая характер изменения функции на графике, выбрать вид аппроксимирующей функции, а на вкладке Параметры задать дополнительные параметры, в том числе установить флажок Показывать уравнение на диаграмме.
После выполнения приведенных операций на диаграмме будет отображена линия тренда (графическое отображение аппроксимирующей функции), а также аппроксимирующая функция в аналитическом виде.
Рассмотрим процесс получения аппроксимирующей функции на примере.
Пример 1.21 Имеются сведения о величинах страховых выплат по годам, представленные в таблице. Требуется исследовать характер изменения величины страховых выплат и подобрать аппроксимирующую функцию (таблица 1.6.).
Таблица 1.6
Год |
Сумма страховых выплат (руб.) |
1 |
150 000 |
2 |
200 000 |
3 |
300 000 |
4 |
450 000 |
5 |
450 000 |
6 |
420 000 |
Решение
В ячейки рабочего листа введем исходные данные в виде таблицы (рис. 1.27).
Рис. 1.27
По данным таблицы, полученным экспериментально, построим график. На графике видно, что экспериментальные данные вначале растут, а затем убывают и есть только один экстремум. Следовательно, в качестве аппроксимирующей функции следует выбрать полиноминальную функцию третьей степени (рис. 1.28).
Рис. 1.28
Откроем контекстное меню и выберем пункт Добавить линию тренда.
В диалоговом окне Линия тренда на вкладке Тип выберем Полиномиальная и установим Степень, равную трем. На вкладке Параметры установим флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации R2.
После щелчка на кнопке ОК на диаграмме отобразится линия тренда и аналитическая запись аппроксимирующей функции
y = - 9259,3x3 + 6E + 07x2 – 1E + 11x + 7E + 13, R2 = 0,9818 (рис.1.29)
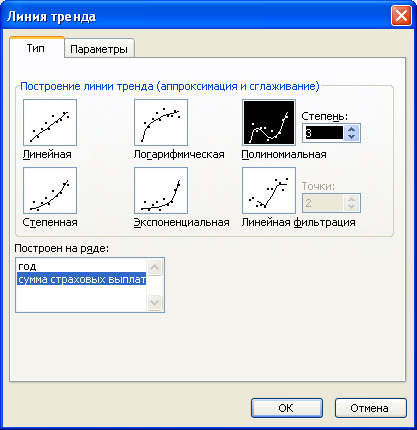
Рис. 1.29
Величина R2 близка к единице, следовательно, степень достоверности аппроксимации является высокой.