3.3. Диалектика части н целого

Исследование закономерностей целостности и иерархической упорядоченности. Выше (гл. 1) были рассмотрены закономерности, характеризующие сложное взаимодействие системы и ее частей, -закономерность целостности (эммерджентности) и связанные с ней закономерности (аддитивности, прогрессирующей систематизации, прогрессирующей факторизации), закономерность иерархической упорядоченности, в которой закономерность целостности прояв­ляется на каждом уровне иерархии.

Основная суть закономерности целостности качественно заклю­чается в отличии свойств системы от свойств ее элементов, с одной стороны, и в изменении свойств элементов, включенных в систему, с Другой. Попытаемся исследовать эту проблему, используя рассмат­риваемый информационный подход.

Прежде всего, обратим внимание на зависимость представления об объекте от информации восприятия (3.81), и в частности, от при­нимаемого при вычленении элементов "кванта" Ai4. Чем больше мы квантуем объективную непрерывную реальность, т. е- чем более мелкие элементы выделяем в системе, тем согласно (3.81) большую информацию мы о ней получаем.

По этой причине человечество все больше и больше дробит свою науку на уз­коспециальные области знаний, увеличивая информацию до такой степени, что Похоже уже не в силах переварить ее.

205

Однако увеличивает ли рост числа элементов точность систем ного моделирования бытия? С одной стороны, вроде бы увеличу вает, поскольку воссоздает все более тонкую структуру. Но, с дру гой стороны... Уместно вспомнить, что в исходном континуально”” объекте все было связано со всем, стало быть, разделив ее на две части, мы должны учесть одну связь между ними, а разделив на три части, учесть уже три связи и т. д. В общем случае представления системы из т„ элементов мы должны учесть число связей, равное числу сочетаний из ту по 2, т. е. т^ = 0,5 my(ms - 1), причем это число растет гораздо быстрее, чем wig.

Для учета этих связей, например, между науками, нам потребовалось бы огроы. вое число "стыковочных" наук типа физической химии, биозлектроники, элскгро. гидравлики и т. д. Между тем, углубляя знания в пределах своей науки, спида. листы мало склонны изучать взаимосвязи наук. Во всяком случае число реально развивающихся "стыковочных" наук гораздо меньше числа "основных" наук, ход для полноты исследования действительности должно быть наоборот, В результате теряется целостность знания о природе, и оно становится тем превратнее, чем боль­ше создается узкоспециализированных наук.

Если оценить относительную точность системы знаний как от­ношение числа имеющихся наук к числу возможных наук, включая "стыковочные", то в идеале она должна бы составлять 5о = 1, а в действительности, поскольку "стыковочные" науки почти отсут­ствуют, то 5 = m^nia + ть) = V(m, + 1), т. е. значительно меньше единицы и продолжает убывать.

Конечно, часть межнаучных связей может оказаться не столь существенной и ею можно пренебречь, но все же остается еще очень много неведомого на стыке нау”, а главное, некому выделить противоречия в данных отдельных наук, без чего невоз­можен синтез целостности.

По этой причине, достигнув изумительных результатов в уз­коспециализированных областях природоведения, мы все еще малс знаем о природе как целом, а грандиозные свершения в сфере пре­образования природы, которые строго соответствуют рекоменда циям специальных наук, нередко приводят к неожиданным и даж опасным последствиям для природы в целом.

С этой точки зрения древние, не успев еще расчленить свои зна. ния о природе на отдельные науки, чувствовали природу как цеяо“, пожалуй, не хуже нас, а энциклопедисты и натурфилософы пони­мали необходимость целостного воссоединения всего знания в о?. ном человеке или в одной науке. Этому учит и теория систем, пер­вейшей заповедью которой является утверждение о том, что сумйа свойств частей не есть свойство целого, т. е. что простая сумма знаний, добытых всеми науками о природе, не есть знание о пр“-роде как целом. Таким обобщающим знанием должно быть мир< воззрение, которое, хотя и формируется на базе специальных ³¹^ ний, но не является простой их суммой, а представляет продукт ся -

206

ясного синтеза, диалектическое единство наук, где центральное мес-jo занимает философия - носительница целостного знания о мире. Однако для успешного выполнения этих своих функций в наше вре-уя ей необходимо сближение с натурфилософией в языке и симво­лике.

Необходимо также отметить, что искусство всегда успешнее справлялось с пере­дачей целостности природы, нежели наука. Деятели искусства прекрасно отдают се­бе отчет в том, что, помимо овладения соответствующей техникой, достаточной для ремесленника, художник должен иметь еще талант претворять систему технических приемов в целостное впечатление, которое одно только и является целью искусства.

Сказанное позволяет дополнительно обосновать необходимость включения в число характеристик системного анализа обязательной ориентации на мировоззренческие представления и использования при моделировании сложных развивающихся объектов не только методов формализованного представления систем, но и методов, позволяющих использовать интуицию и опыт специалистов, кото­рые и являются носителями целостного восприятия, отражаемого в системе ценностных ориентации и в системе предпочтений, если часть ценностных ориентации удается формализовать.

Далее, исследование соотношения (3.95), символически отобра­жающего закономерность целостности, позволяет обратить внима­ние на тот факт, что суммарная собственная сложность элементов в устойчивых системах больше, чем системная, т. е. С„ > С^. Большим, нежели С,,, может быть и С..

Например, сложность телевизора С; для пользователя меньше сложности его конструкции С, и суммарной сложности С, (возможностей) элементов, из которых собран телевизор. Так что иногда бытующее выражение "целое больше своих частей" не следует понимать буквально. Количественно содержание целого может быть меньше, но качественно его свойства принципиально новы по сравнению со свойствами его элементов.

Ранее проводимые качественные исследования закономерности целостности (эмерджентности) всегда уделяли большое внимание изучению причин изменения свойств системы по сравнению со свойствами составляющих ее элементов. Соотношение (3.96) позво­ляет указать на взаимное содержание Св как на непосредственный носитель целостности.

Системы можно сравнивать между собой по всем видам слож-ти. Можно говорить о различной сложности системы в целом. [ожно сравнивать суммарные возможности элементов разных си-•ем. Можно сопоставлять как бы общую сложность конструкций, генивая Св.

Разумеется, эти оценки нужно рассматривать как относитель­ные. Взятые сами по себе, они ни о чем не говорят. Иными словами, оценки Сс, Со, Св и другие информационные оценки применимы лищь для сравнительного анализа систем, их элементов, структур, конструкций и т. п. , 207

^ <? <? У <П.

Следует оговорить, что оценки! С,;, С„ С, могут интерпрет ваться по-разному, т. е. применяться для оценки как бы по раз ^^0-ным критериям. ¹¹¹¹"

Например, С, можно рассматривать ксак сложность конструкции, схемы технических систем), сложность структуры (для организационзидх), а можно мощью С, оценивать степень взаимосвязашности элементов в систем, котопуш ^п^ технических (а иногда и для организационщых) систем можно шггерпрстироватт,^ая' характеристику устойчивости системы, а доля органюационныз - как меру ца"¹ ности, т. е. как количественную оценку дни сравнения стеценж проявления в си⁰⁰' ме закономерности целостности. ^с11'

При различной сложности элеиентных баз сравнительный ана лиз с использованием оценок С. может дать неверный результат поскольку С, простенькой схемы (структуры) с большим числом элементов может оказаться таким же, как у сложной схемы (структуры) с малым числом элементов, но с с ильными и слож­ными связями между ними. Поэтому удобнее пользоваться относи­тельными характеристиками, приведенными к единице сложности элементной базы.

Разделив члены выражения (3.96) на С„ получим две важные сопряженные оценки:

а=-С,/Со; (3.100) Р=С/С; (3.101)

причем р = 1 - а.

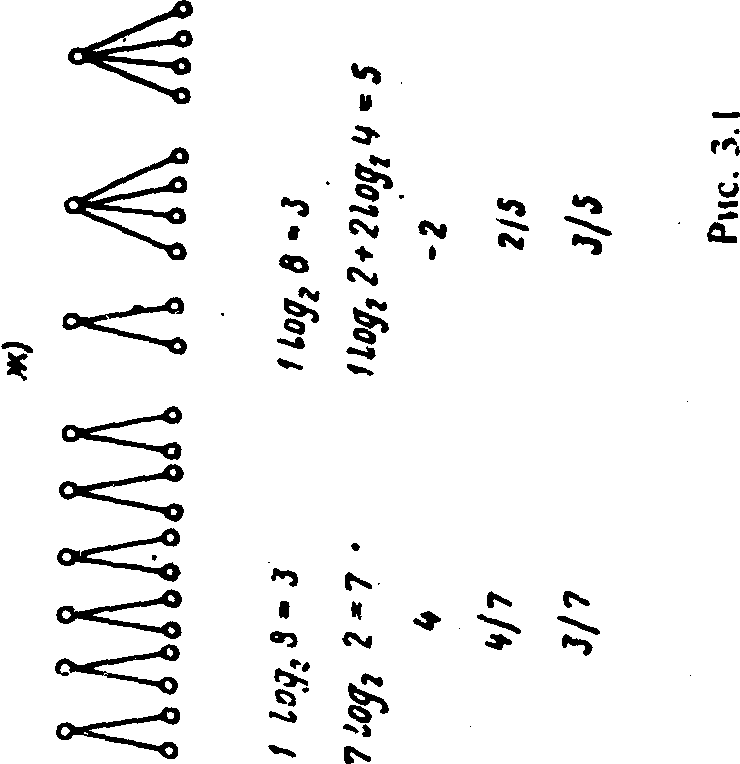
Первая из них (3.100) характеризует степень икяостности, связ­ности, взаимозависимости элементов системы; для организацион­ных систем а может быть интерпретирована как характеристика устойчивости, управляемости, степени централизации управления.

Вторая (3.101) - самостоятельность, автономность частей в це­лом, степень использования возможностей элементов. Для органи­зационных систем р удобно называть коэффициентом использова­ния элементов в системе.

Знак минус в выражении (3.100) введен для того, чтобы а было положительным, поскольку С, в устойчивых системах, для которых характерно Су > Сг, формально имеет отрицательный знак. Связан­ное (остающееся как бы внутри системы) содержание С, харакгери- < зует работу системы на себя, а не на выполнение стоящей перед ней цели (чем и объясняется отрицательный знак С.).

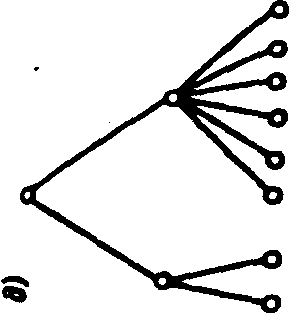
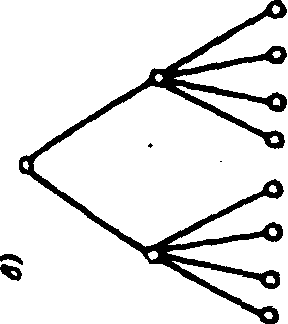
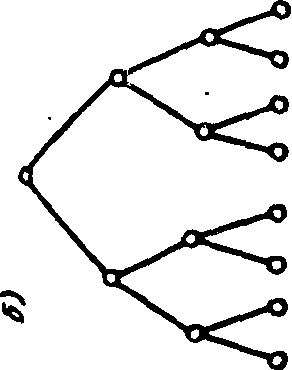
Последнее важно учитывать при формировании структур сч¹ тем. Поэтому приведем упрощенный пример сравнительного аналг за иерархических структур (рис. 3.1), которые могут отобран”¹ либо схемы ко1“емутаций верхнего узла технической системы с^эл ментами нижнего уровня, либо варианты организационной crpy¹ туры системы управления, включающие разное число заместителе' ^

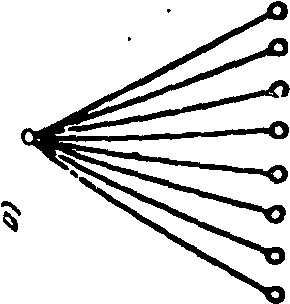
директора (второй сверху уровень иерархии) и подчиненных цм управленских подразделений.

Предположим. что целью всех этих структур является выбор цз 8-ми элементов нижнего уровня структур. При наличии элемента способного осуществлять выбор из 8-ми. задача решается с по. мощью угого элемента, приведенного на рис. 3.1 и. Если же такого элемент це существует, то задачу можно решить с помощью, эде. ментов, обладающих меньшими способностями - ключей, с пери. ключен^ями для выбора из 4-х или из 2-х положений, или помощ­ников, Распределяющих между собой ответственность за выбор ис­полнителей решения (варианты структур приведены на рис. 3.1 б-д).

В изображении иерархических структур способ вычленения эле-ментов це определен, и их "читать" можно неодинаково. Так, эле­ментам^ можно считать каждую ветвь иерархической структуры (каждое положение ключа или каждое структурное подразделение), полагая, q-го ветвь имеет два возможных состояния ("участвует" -"не участвует" ц принятии решения по выбору), т. е. Л/1 = 1 ветвь, а минимальная единица информации J = 1 бит. А можно разделить структуру на элементы с учетом того, что основной функциональ­ный элемент, осуществляющий выбор, - узел, и тогда элементами будут наборы узлов, приведенные на рис. 3.1 с - п для структур рис. 3.1 о ^А о соответственно, и тогда Л/1 = 1 узел (или ключ), а каждый элемент также будет оцениваться минимальным значением J = 1 бит. но <: разными "способностями", которые оцениваются числом ветвей, подчиненных узлу (или состояний ключа), отражаемых в оценке /у. Тогда при равновероятном выборе для узлов с двумя состояниями Н = log? 2 = I бит, для узлов с 4-мя состояниями Я= log.. 4= з бита и т.д.

^'РЧвнительные оценки вариантов структур, предназначенных для достижения одной и той же цели - выбор из 8-ми состояний нижнего уровня иерархии - приведены на рис. 3.1. При расчете С система рассматривается как один элемент, т. е. J, принимается равной единице.

Сопоставляя структуры с использованием прлведенных на рис. 3.1. оценок, можно сделать, например, следующие выводы. Если выбирался оргструктура предприятия, то оценку а можно тракто­вать ка^ устойчивость системы, степень сохранения ^'целостности. а оценка р _ как коэффициент использования возможностей элемен­тов. их свободу. Иными словами, увеличение (3 можно трактовать как децентрализацию управления, а а - как степень централизации управления. Тогда при стремлении к демократизации, децентрали­зации Управления, к более эффективному использованию возмож­ностей Сотрудников или структурных подразделений, предоставле-210

^ им большей самостоятельности следует выбрать структуру, "деденную на рис. 3.1 в. А при стремлении сохранить целостность 'дприятия, усилить централизованное управление следует отдать ^г почтение структурам, приведенным на рис. 3.16, а из двухуров­невых структур - рис. 3.1г.

Выбранный вариант структуры будет содействоватг или, напротив, препятство­вать проведению ^{в жизнь} принятых принципов управления, т. е. как бы не етремил--д пуководитель предоставить больше самостоятельности структурным подразделе-у„,и и сотрудникам структуры рис. 3.16 и г будут препятствовать проведению этой политики.

Исследования структур с различным числом уровней иерархии показало, что по мере увеличения числа уровней степень целост­ности существенно возрастает: в двухуровневых структурах а ко­леблется вокруг значения 0,5, а в структурах с числом уровне 5-6 и более а приближается к 0,9, т. е. существенно возрастает связан­ное, остающееся как бы внутри системы Св, характеризующее ра­боту системы как бы на себя. Последнее важно учитывать при фор­мировании структур систем.

Чем более сложной и многоуровневой становится организационная структура предприятия, тем в большей мере она будет работать "сама на себя". Аналогичная ситуация была замечена при создании банков данных: при стремлении к универ­сальности БД и усложнении его системно-логической структуры и СУБД типовые БД, создаваемые в АСУП для отображения информации о производственных систе­мах (типа СИОД, БАНК и т. п.) становились неэффективными, в них требовалось все больше ресурсов для поддержания собственных СУБД, т. е. БД начинал в боль­шей мере работать "сам на себя".

Возрастает степень целостности а и при увеличении числа со­ставляющих второго сверху уровня иерархической структуры.

Например, в организационнвх структурах при увеличении числа заместителей директора, что также подтверждается практикой.

Наименьшая централизация характерна для наиболее неравно­мерной структуры (рис. 3.1д). Однако у подобных структур, когда одной из вершин подчинено существенно большее число составля­ющих, чем другой, есть существенный недостаток: малая разница в оценках Н, которые в данном случае удобно трактовать как потен­циал, значимость, характеризующие влияние соответствующей вер­шины на принятие решений.

Так, в варианте структуры рис. 3.1г крайне малое различие потенциалов си­стемы в целом (Не ⁼ 3 бита) и вершины, которой подчинено 6 составляющих (//; = 2,7 бита), приводит к тому, что помощник, возглавляющий последнюю вершину, Начинает вести себя практически независимо от руководителя системы в целом. Этот Недостаток довольно часто проявлялся на практике, но его пытались объяснить квалификацией и авторитетом соответствующих руководителей, в то время как Информационный анализ структур показывает, что это характеристика структуры, а

Яс частного лица.

211

Обратим внимание на тот факт, что пример сравнительного анализа рассмотренных вариантов иерархического представления одной и той же системы (предназначенной для решения задачи вы­бора из 8-ми элементов нижнего уровня) иллюстрируют возмож­ность нахождения системы между двумя крайними состояниями ~ абсолютной целостностью (рис. 3.1 а) и аддитивностью, расчленени­ем системы на независимые части, что возможно осуществить раз­личными способами (рис. 3.1 е - и), и соответственно в зависимос­ти от способа выделения частей одна и та же система может харак­теризоваться различной целостностью.

Можно, например, расположить варианты иерархического представления сис­темы в порядке возрастания или убывания степени целостности, т. е. появляется возможность оценки предложенных А.Холлом закономерностей прогрессирующей систематизации и прогрессирующей факторизации.

Эта особенность системного анализа сложных объектов путем представления их различными элементами принципиально отличает методологию системного исследования от методов формализован­ного представления, используемых для исследования и проектиро­вания технических систем, собираемых из вполне конкретных дета­лей и узлов. При этом легко видеть, что в случае модификации де­талей и комплектующих, например, при сборке автомобилей, полу­чаются различные модели автомобилей, качественно отличающиеся друг от друга, т. е. и в этом примитивном изменении элементов получается качественно иная целостность. В случае же сложных си­стем с неопределеннностыо, когда "...объект не имеет свои части готовыми, данными" [2.1], а мы образуем их в процессе исследо­вания, анализ диалектики части и целого с использованием инфор­мационного подхода приобретает особо важное значение, помогает понять, что расчленяя систему по-разному мы фактически получаем качественно различные варианты представления целостности, что и объясняет возможность использования иерархических представле­ний как средства исследования сложных систем с начальной неоп­ределенностью.

В связи с этим необходимо напомнить, что иерархические пред­ставления систем могут быть не только древовидными. В этом слу­чае расчет информационных оценок будет иным.

В случае иерархических структур со "слабыми" связями элемен­ты, подчиняющиеся двум или более узлам вышележащего уровня, можно как бы "расщепить", подчинив их части разным вышележа­щим узлам; тогда можно проводить расчеты аналогично рассмот­ренным.

При этом целесообразно относительно оценить "расщепляемые" составляющие. что в случае оценки, например, организационных структур линейно-функциональ­ного типа можно оценить численностью управленческого персонала, занимают'" гоея выполнением частей "расщепленной" функции.

212

В случае, если такие оценки не удается получить, либо реальные процессы необходимо представлять иерархическими структурами типа "страт" или "эшелонов", либо большое число и разнообразие связей между компонентами системы приводит к "проклятию раз-щерности", следует использовать полевое описание системы в про­странстве ее структуры.

Тогда, обозначив через N "мощность" объекта управления, имея в виду его способность производить любого рода продукцию, включая информационную, в соответствии со своим назначением, и через г плотность N в каждой точке соответствующего простран­ства, потребуем, чтобы с учетом ограничений на пропускную спо­собность системы управления потенциал Н в каждой точке был максимален:

1 rRp I (RdN --j——=——J——— ->max, (3.102)

ff=-

3.W • ”• hit • Г

\л' г 4я" г где г - число инстанций между данной точкой и каждой остальной в пространстве управления; R - доля общего числа функций объекта, участвующих во взаимодействии с каждой точкой. Это обеспечи­вает максимальную управляемость и связность (целостность) си­стемы, и тем самым и выбор наилучшего варианта структуры си­стемы управления. С примерами такой оценки произвольных струк­тур разного вида можно познакомиться в [2.4].

Наряду с рассмотренными оценками, характеризующими струк­турные особенности систем, взаимоотношения частей и целого, ча­сто бывает полезно оценить систему и ее структуру с точки зрения затрат труда на принятие решения в процессе функционирования системы. В частности, большинство управленческих решений связа­но с выбором исполнителя или адресата из числа сотрудников, под­чиненных той или иной вершине оргструктуры.

Так, определяя, до сведения каких ио подразделений или отдельных сотрудников нужно довести соответствующую директивную или отчетную информацию, ЛПР затрачивает труд на прочтение хотя бы заголовков распределяемых документов, на сопоставление их с наименованиями подчиненных подразделений (или с темами, выполняемыми подчиненными ему сотрудниками), т. е. на переработку опреде­ленной информации (которую можно оценить в буквах, словах, абзацах).

Таким образом, реальные затраты управленческого труда, т. е. фактический смысл (сложность) задачи Сф, превосходят ее струк­турный смысл во столько раз, во сколько раз ее фактически пере­рабатываемая для принятия решения информация J^ превосходит (структурную J

j Сф=^ 7фЯ,, (3.103)

213

где Н, - сущность (потенциал 1-го элемента структуры; Jф - инфор­мация, перерабатываемая тем же элементом (которая определяется с учетом числа состояний элемента, т. е- числа подчиненных ему со­ставляющих) и числа выполняемых заданий.

Суммарная оценка затрат труда на принятие решений (выбор) при прохождении по структуре сверху вниз важна не только при оценке оргструктур, но и при определении структур баз данных, алгоритмов поиска информации в них.

Для оценки систем можно использовать характеристику полеэ-ной производительности (информационной мощности) N (3.99).

Можно также ввести коэффициент полезного действия t| струк­туры, определяя его с учетом полных возможностей структуры С^ и используемых ее возможностей С с точки зрения конкретной цели:

(3.104)

Дело в том, что, с помощью приведенных на рис. 3.1 иерар­хических структур можно осуществлять выбор не только из элемен­тов самого нижнего уровня иерархии, но и из элементов любого другого уровня (например, в структуре рис. 3.16 - выбор из элемен­тов второго снизу уровня, или из элементов второго сверху); тогда С^ будет больше оценок, приведенных на рис. 3.1, и можно опре­делять к.п.д. г\ соответствующей структуры.

Еще раз оговорим, что оценки Сс, Со, С” и другие информаци­онные оценки применимы лишь для сравнительного анализа систем, их элементов, структур, конструкций и т. п. При этом необходимо следить за тем, чтобы условия сравнения, принимаемые единицы измерения J и Н (логарифмические, безразмерные), критерии срав­нения, для оценки по которым используются Сс, Со, Св, были оди­наковыми.

Следует также отметить, что оценки Н, С, а, Р зависят не толь­ко от вариантов структуры системы, но и от индивидуальных осо­бенностей руководителя, принятых им принципов "вмешательства" в дела нижележащих уровней управления.

Если директор распределяет задания только между своими заместителями, не вникая в то, имеют ли они в своем подчинении подразделения, способные выполнить эти гадания, то его вклад в принятие управленческих решений следует оценивать исходя не из 8-ми элементов нижнего уровня, а из числа подчиненных ему непосред­ственно заместителей (тогда его Н в вариантах бив рис. 3.1 будет одинаковым log 2 = 1 бит, а в варианте г - log 4=2 бит). Соответственно изменятся и оценки С, а, Р.

От выбранного подхода к управлению зависит также относи­тельный вклад верхнего узла в затраты труда на принятие решении (на "один проход" по структуре сверху вниз), который может hcj пользоваться как еще одна характеристика для сравнительной оценки структур. 214

Так, при влиянии только на непосредственных подчиненных вклад руководите­ля (директора, президента компании и т. п.) во всех вариантах будет меньше по сравнению с первоначальным подходом к оценке структуры, при котором предпола­галось. что директор хорошо знает возможности всех контролируемых им подразде­лений (или даже подчиненных, т. е. возможности элементов самого нижнего уровня структур) и использует эти знания при принятии решений.

Особенности моделей диалектической логики. Как отмечалось выше, проблему системного моделирования объектов и ситуаций с неопределенностью с точки зрения информационного подхода мож­но представить в форме дискретной модели непрерывного бытия, отражающей диалектический синтез взаимно исключающих друг друга требований точности и обозримости, а задачей прикладной системологии и системного анализа является выработка средств достижения такого компромисса между "проклятием размерности" и высокой точностью системного моделирования актуальных задач практической деятельности человека.

Для понимания сути такого моделирования и возможностей ин­формационных моделей обратим внимание, прежде всего, на прин­ципиальное различие в подходе к числу в математике и в повсе­дневной практической деятельности. Если для математиков число 3 означает 3 абсолютно и безусловно одинаковые единицы, принци­пиально неразличимые между собой, то в практической деятельно­сти любого рода мы пользуемся именованными числами, которым придаем совершенно иное значение и смысл.

Так, 3 человека в силу неустранимой индивидуальности заведомо и принципи-мьно не идентичны друг другу, 3 яблока также не абсолютно одинаковы, а каждый ¹⁰ ^-х кг сахара представляет собой 1 кг с точностью до погрешности взвешивания.

Математическое число представляет собой высшую, предель-"Ую степень абстракции количества, которой не соответствует ни-I какое реальное, т. е. измеряемое, ощущаемое количество. Действи-т^льно, числа в математике всегда задаются с абсолютной точ-"•^стью, никогда не достижимой в реальной действительности, и тем ^МЫм обретают статус абсолютной истины, к которой только и "Рименим логический закон исключенного третьего, т. е. выражае-^мое математическим числом количество либо - истинно, либо -^Жно, а третьего быть не может.

Между тем, в реальной действительности приходится иметь де-^л0 только с относительными, хотя и объективными, истинами, в ^^гности, каковыми именованные числа, всегда получаемые с ко-"^чной точностью. В силу этой относительности, приближенности, "^Нованные числа не удовлетворяют закону исключенного третье-' Поскольку двукратное измерение одного и того же количества '^за погрешности измерительного прибора обычно приводит к У¹^ различным результатам, выражаемым различными именован-^1л1и числами, но имеющими статус одинаковой (не абсолютной!) 215

истинности, с точностью до погрешности ± Лх (т. е. результат из­мерения именованного числа л- ± Ах), что и учтено в информацией. ной оценке J согласно (3.81).

Иными словами, именованные числа - это вовсе и не числа в математическом смысле, а диапазоны возможных значений тех или иных количеств, или в терминологии Заде - размытые числа, в луч­шем случае соответствующие среднему значению многократных измерений. Именно поэтому в ряде приложений важно использо­вать оба способа (детерминированный и вероятностный) измерения

JuH.

Размытость делает именованное число диалектическим объек­том, способным развиваться, уточняться по мере совершенствова­ния способов измерения и выражающим единство противоположно­стей, существующих в одно и то же время и в одном и том же отно­шении.

Так, 3 кг сахара - это и 3, поскольку приблизительно соответствует истине, и не 3, поскольку в какой-то мере (с точностью до погрешности взвешивания) ей не соот­ветствует.

Свойство размытости придает именованным числам сходство с понятиями, выражаемыми словами живой речи, поскольку они так­же всегда размыты.

Так, понятие "рост человека" размыто по всему диапазону возможных значений длины человеческого тела от лилипутов до гигантов и вполне может быть выраже­но именованным числом 170 ± 100, где 170 см - средний рост человека, размытый в диапазоне от 70 до 270 см.

Что же касается математических чисел, то это метафизические объекты формальной (математической) логики, не способные со­вершенствоваться, уточняться в силу своего абсолютно истинного статуса, содержание которого не может быть выражено словами (если не считать словесного наименования числа, тождественного цифровой записи и имеющего всегда единственное абсолютно точ­ное значение).

Важно также обратить внимание на тот факт, что в своем наи­меновании именованное число несет признак качества, что роднит его с понятиями гуманитарных наук и философии, но в отличие от них дополнительно сужает объем соответствующего понятия до рамок ошибки измерения.

Действительно, 3 кг означают не только массу вообще, но возможные ее зна­чения в диапазоне 3+6. где 8 - ошибка весов, так что огромный объем понятия "масса" сужается до величины Ло ⁼ 25/Л, где Д - минимально различимое ее значе­ние, причем в частном случае Л = 28, п„ = 1. Таким образом, синтез частных нау” идет в направлении формирования именованных чисел, выражающих противоречи" вое единство, компромисс всеобщности и точности.

На чувственном уровне противопоставление этих категорий весьма относительно и условно, преобладает их целостное, систем

216

цое восприятие и взаимный переход друг в друга. Однако стоит нам абстрагироваться от конкретной реальности, как сразу же возника­ет два противоположных направления движения, одно из которых в конце концов ведет к философии, а другое - к математике, как пре­дельно абстрактным наукам.

Первое из направлений - очевидный и последовательный путь последовательных и безграничных обобщений, ведущих через поня­тия частных наук к всеобщим философским категориям. Характер­ная особенность этого направления - последовательное возрастание размытости понятий, охватывающих по мере обобщений все боль­ший и больший объем реальных явлений и ведущее к категории материи, охватывающей весь безграничный объем данной в ощу­щениях объективной реальности и в силу этого бесконечно размы­той во всех свойствах, кроме свойства существовать и отражаться, поскольку последнее присуще всей реальности.

Поскольку размытость эквивалентна погрешности задания именованного числа философские выводы, имеющие сравнительно большую размытость (погрешность), применимы лишь в среднем с учетом принципа конкретности истины. Более того, размытость философских операций делает бессмысленными какие бы то ни было логические операции над ними, поскольку их результат будет также размытым, приближенным.

Так, ввиду относительности всех парных категорий вроде формы и содержания, покоя и движения и т. д., к ним бессмысленно применять логический закон исклю­ченного третьего, ибо форма всегда содержательна в большей или меньшей степени, а содержание не существует без той или иной формы, не говоря уже о том, что дви­жение и покой полностью обратимы и зависят от точки зрения наблюдателя. Однако именно из-за размытости на всю реальность философия говорит на языке этой ре­альности и является наукой обо всем сущем.

Иное дело противоположное направление абстрагирования, ведущее по пути последовательного уточнения, по пути уменьшения размытости именованных чисел. При этом реальность все больше вытесняется за рамки размытости и в пределе оказывается полнос­тью вне математического числа, воплощающего абсолютную точ­ность. Действительно, реальные качества существуют лишь в рам­ках объективной размытости, конечной точности задания.

Именно поэтому абстрагирование путем бесконечного уточнения приводит к полному вытеснению из числа каких бы то ни было реальных качеств и делает мате-'•“'гаку, оперирующую числами, строго говоря, наукой ни о чем (вспомним, как выло отмечено в гл. 2, по выражению С.Лема "математики изгнали беса значение из евоих пределов"). Действительно, с математической точки зрения объем понятия п, "Мела, например 3, равен нулю, поскольку ошибка 8=0.

Но, с другой стороны, абсолютная точность объектов матема-^и позволяет применить к ним ряд столь же абсолютно точных "Равил преобразования, сохраняющих абсолютную точность ре-217

зультата. Совокупность таких правил сводится к формальной лощ. ке, ощутимо облегчающей рутинные операции, а главное, легкп реализуемой посредством кибернетической техники, что, на первци взгляд, делает математику в прикладном плане более актуальной чем философия.

Так оно и было, пока математизации подвергалась и автомати­зировалась сравнительно простая, но трудоемкая рутинная деятель­ность в проектировании или управлении предприятиями и органи­зациями. Однако практика потребовала формализации и автомати­зации все более сложной творческой деятельности, связанной с принятием решений в условиях неопределенности, размытости и даже противоречивости исходных данных, да еще на основе проти­воречащих друг другу критериев.

Специалисты-математики знают, что такого рода задачи во­обще не поддаются строгому математическому анализу из-за прин­ципиальной неприменимости к ним логического закона исключен­ного третьего. В этих размытых условиях именно философский анализ, диалектическая логика могут дать универсальный аппарат творческой деятельности, приемлемой для кибернетической техни­ки. Для реализации такого подхода можно было бы, во-первых, создать специальные логические машины, оперирующие именован­ными числами на основе диалектической логики, и, во-вторых, все гуманитарные науки (и философия) должны бы научиться говорить на языке именованных чисел, приемлемых и для обычных ЭВМ, что представляется вполне реальным ввиду близкого родства между словом и именованным числом.

Об актуальности синтеза диалектико-материалистической мето­дологии, т. е. философского содержания и математической формы, свидетельствует и проблема достоверности новых научных резуль­татов. Хотя в качестве критерия истины должна выступать практи­ка, подтверждающая или опровергающая соответствующие нова­ции, но, не говоря уж об относительности критерия практики, по­следняя в большинстве случаев требует больших затрат времени и нередко огромных средств для постановки экспериментов, что за­ставляет искать пути априорного по отношению к практике теоре­тического установления истины. Обычно это делается посредством формально-логического анализа, а то и просто сопоставлением математических соотношений, вытекающих из новой теории, с со­отношениями, характерными для господствующей парадигмы. В случае расхождения результатов в соответствии с законом исклю­ченного третьего делается вывод либо о неполноценности господ­ствующей парадигмы, либо об ошибочности новой теории.

Это нередко приводит к отрицанию, неприятию или даже "запрету" нового, как было с кибернетикой, генетикой, голографией, автоволновыми химическими реакциями, что наносит прямой хозяйственный ущерб.

218

Между тем, осознание размытости, относительной истинности осподствующей парадигмы и ее формального аппарата могло бы в „чках закона единства противоположностей, если не примирить, ' по меньшей мере оградить последнее от запретительства в ожи­дании широкой практической апробации.

С этой точки зрения крайне необходимо подчинение формального аппарата воясой теории отмеченному К.Марксом в послесловии ко второму изданию "Ка­питала" требованию диалектики: "В позитивное понимание существующего ова включает в то же время понимание ее отрицания, его необходимой гибели, “ахдта осуществленную форму рассматривает в движении, следовательно, также и с ее „походящей стороны, ибо она ни перед чем не преклоняется и по существу сюелу критична и революционна".

Иными словами, в отличие от классической логики, где дизъ­юнкция А и "неА" есть логическая константа, именуемая абсолют­ной истиной, в диалектической логике дизъюнкция противополож­ностей есть относительная истина, являющаяся переменным пара­метром непрерывного процесса познания, движущей силой которо­го выступает борьба, а не отрицание противоположностей.

Итак, философия и математика являют собой итоги, апогей прямо противоположных путей абстрагирования, что, на первый взгляд, делает их объекты далеко отстоящими друг от друга и “е-совместимыми. Именно в предельной якобы оторванности матема­тики от реальности с точки зрения философии и в предельной яю-бы неточности философии с точки зрения математики и лежат кср-ни затруднений на пути математизации гуманитарного знания.

В то же время эти альтернативные пути абстрагирования nfo-тивоположны только в начале, а в конце движения дают нечто весьма схожее, если не одно и то же. Действительно, как качестю, так и количество имеют общую цель: сужение объема понятия "объективная реальность" до объема понятия той или иной специ­альной науки. Но если качество делает это сужение путем отбра(ы-вания всех свойств, кроме одного, интересующего данную науку, то количество еще более сужает объем понятия уже в рамках этого свойства путем отбрасывания всех его возможных значений, креме одного или нескольких, представляющих конкретный интере< в данное время и в данном отношении. В результате появляется име­нованное число, отражающее объективную реальность, как каче­ственно, так и количественно.

И поскольку количественная данность в реальных условиях всегда размыта в рамках разрешающей способности используемых измерительных средств, то математизация любой науки неизбежно идет по пути фактического отказа от математических чисел (ito далеко не всегда осознается с полной ясностью) и размывания ма­тематических правил обращения с ними.

Те математики-прикладники, которые начинают это осозна­вать, добиваются и наиболее адекватных результатов в решении 219

актуальных проблем, которые с точки зрения чистой математики как отмечают сами математики' сформулированы некорректно.

Разумеется, когда речь идет о материи, т. е. о беспредельно раз­мытой категории, ее количественная данность тоже беспредельно размыта и в принципе могла бы быть выражена только беспредель­но размытым именованным числом, если бы не беспредельная раз­мытость самой размерности материи, делающая неприменимым к ней размерные величины.

Однако для другой универсальной категории, продукта отраже­ния материи - информации - характерна как размытость, так и без-размерность, и ее количество зависит от разрешающей способности (точности) наших органов чувств и дополняющих их измеритель­ных приборов.

Преимущество информации по сравнению с просто именован­ным числом состоит в том, что она непосредственно зависит от точности измерения. Если, имея именованное число 3 кг, ничего нельзя сказать о точности измерения, то количество информации согласно (3.81) прямо зависит от точности задания АА (кг, г, л<г, л”, дм, см и т.д.), и поэтому может быть различным, зависит от кон­кретных целей моделирования.

Вообще, если материя не исчезает и не возникает, но лишь пе­реходит из одной формы в другую, что фиксируется законом сохра­нения материи, то информация об одной и той же форме материн можно получить сколь угодно. Именно это ее свойство позволяет нам делиться информацией с другими людьми, самим ее не лишаясь. При этом количество информации все время растет, но так назы­ваемая безызбыточная информация, которая содержится в первоис­точнике, остается одной и той же, и именно только она и адекватна отражаемой материи в количественном отношении.

Информация - диалектический объект не только в силу размы­тости, но и в силу способности эволюционировать, например, уве­личивать свое количество по мере совершенствования измеритель­ных приборов, служащих средством ее получения. По этой причине к ней применимы законы классической и формальной логики за исключением законов тождества и исключенного третьего, а также вытекающих из них следствий. Вместо них к информации примени­мы законы единства противоположностей и отрицания отрицания. что и позволяет учесть в рассматриваемых информационных моде­лях символически учэсть как развитие, так и метафизически не­совместимые противоположные требования.

В этих условиях вполне уместно говорить о символической диа­лектической логике как универсальном орудии решения реальных

' Тихонов А.Н. и др. Регуляризирующие алгоритмы и априорная информация. -М.: Наука, 1983.- С. 5. 220

прикладных задач, носящих неопределенный (размытый) характер, что делает этот синтез философской размытости и некоторых логи­ко-математических закономерностей, дополненных законами диа­лектики, куда более актуальным и эффективным, нежели метафи­зические строгости чистой математики.

Замена математического числа информацией (размытым чис­лом), т. е. замена абсолютно истины относительной, позволяет использовать символическую запись любых суждений в форме сим­волических уравнений (или неравенств) типа (3.89), (3.98), к которой применимы почти все правила математических преобразований за вычетом тех, что следуют из закона исключенного третьего, заме­няемого в этих соотношениях законом единства противоположно­стей.

При формировании таких систем уравнений возникает вопрос, сколько же информации можно получить об объекте, если распола­гать идеально точным прибором? На первый взгляд согласно (3.81) можно получить бесконечно много информации, поскольку идеаль­ный прибор должен иметь погрешность АД = 0, однако следует учесть, что любое материальное свойство существует как таковое лишь в рамках конечной точности, или размытости, нечеткости.

Здесь вахно отметить, что реальные объекты нередко имеют установившуюся в процессе эволюции ДЛ. Так, вид в биологии существует лишь с точностью до осо­би, живое существует с точностью до клетки, вещество в химии - с точностью до молекулы, действие в физике - до планковского кванта действия. И никакое уточне­ние здесь принципиально, без потери качества невозможно, хотя, например, молеку­ла может быть разложена на атомы, но последние не являются веществом с хими­ческой точки зрения. Не говоря уже о расчленении особи или клетки. Аналогично результаты творческой деятельности человека, например, музыкальное или живо­писное произведения физически могут быть разложены на отдельные звуки или мазки, но отдельный звук - не музыка, а отдельный мазок - не живопись.

Таким образом, можно сделать вывод, что количество инфор­мации, потенциально содержащееся в материальном объекте, всегда конечно, поскольку соответствующее материальное свойство всег­да реализуется в рамках конечной точности или минимального диа­пазона существования АД. Эту информацию мы будем именовать потенциальной и вычислять как А/&В в отличие от актуальной ин­формации А/&А, снимаемой с реальных приборов. Понятно, что безызбыточная часть потенциальной информации тем самым чис­ленно равна измеряемой материи, точнее конкретного материаль­ного свойства Mic = А/АВ. Отметим, что отношение ЛД/АЛ и пред­ставляет собой информационную проницаемость /?^, фшуриру-ющую в соотношении (3.1).

В то же время обратим внимание на тот факт, что если для объ­ектов естественной природы, в т. ч. биологических, Л/4 формиру­ется в процессе эволюции, то определить это минимально значимое

221

количество информации, т. е. элемент системны, для искусственны систем типа предприятия, государства, при” анализе конкретны. проблемных ситуаций с неопределенность.ию не всегда просто Именно поэтому в конкретных условиях м“юделирования прещд. всего нужно определять АА, для всех учитыва&емых в модели объец. тов или материальных свойств, отражая в этв ой оценке мнения над более компетентных экспертов (что будет проэиллюстрировано в щ 7 на конкретных примерах, и в частности, на “. примере моделировав ния рыночной ситуации).

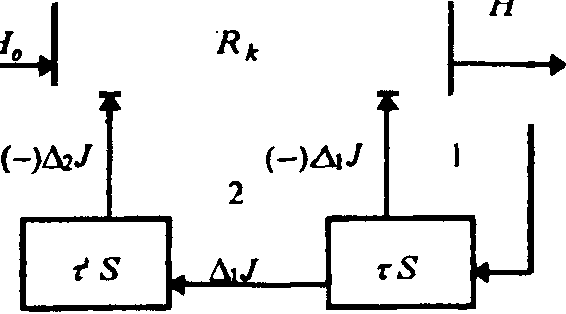
Обратимся теперь к диалектике отражения. Как уже отмена. лось, в основе диалектики лежит отрицание и двойное отрицание (отрицание отрицания). Отрицание прояв-п^яет себя двояко: как внешнее отрицание, т. е. отрицание А посредством "неА" (о чем унц говорилось выше) и как самоотрицание, т. е?. отрицание А измене­ниями, происходящими с самим А. Внешнее отрицание есть вместе с тем отрицание в пространстве, ибо А и " миеА " всегда разобщены территориально, что помимо прочего и позвюоляет судить о них, как о разных вещах; самоотрицание же есть всвегда отрицание во вре­мени, отрицание будущим А его же настоящего и настоящим А его же прошлого, происходящее в каждой точке; пространства, занято­го А. Как внешнее отрицание, так и самоотрицание есть следствие соответственно взаимоотрицания А и "неА" ЛЛ самоотражения А. С учетом диалектики отражения и самоотражегния мы и рассмотрим процесс становления чувственной информации**' воспользовавшись для наглядности структурно-символической сгхемой, приведенной на

рис. 3.2.

На этой схеме стрелки изображают направления потоков ин­формации в процессе отражения, а в квадра*тиках изображены ин­формационные проницаемости, символизирующие способность ор­ганов чувств к отраже­нию материи, а также изменений, происходя­щих с информацией.

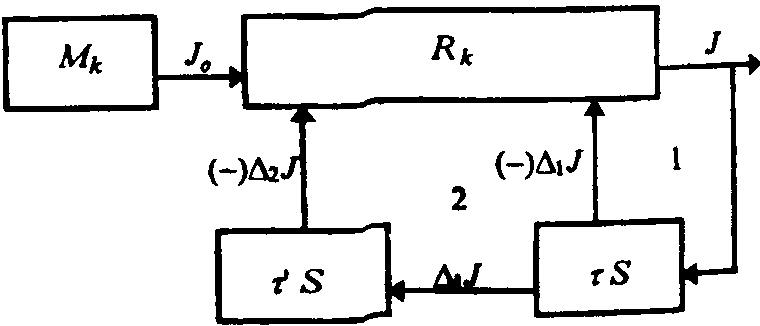
Символ S ради со­кращения записи обо­значает диалектический оператор d/dt, в кото­ром d соответствует процессу отрицания, выраженному в естест­венном языке словом "не". Например, dA е<"гь то же самое, что и "неА". Весь же оператор d/dt содержит в знаменателе еще указание на то, что отрицание происходит во времени, т. е. речь идет о № моотражении, которое противопоставляет А в момент времени ему же самому, но в иной момент, т. е. не и l или dt. 222

pine. 3.2

Итак, материя М^ воздействует на органы чувств и с учетом яльной информационной проницаемости Ric среды должна была ^^е отразиться ими как J^ = R^M^, чему однако препятствуют про­весы самоотражения органов чувств. Действительно, по мере от-ажения будут возникать приращения AJ информации, которые Шляются новообразованиями, чуждыми предшествующей инфор­мации и отрицающими ее, поскольку эти приращения являются 'неА" ^п0 отношению к принятой за А информации в предше­ствующий про-межугок времени. Это обстоятельство на структур­ной схеме символизируют а)у и &2-/, которые вычитаются из по­тенциальной информации /, (знак указан в скобках), хотя и по­рождаются ею же. При этом приращение Ai./ представляет прира­щение информации за характерный промежуток г времени t, так что накопление не /^ за время т дает Ai7, т. е. AiJ = т dJ/dt.

Вместе с тем, поскольку отражение и отрицание идут в общем случае с непостоянным темпом, то \\J само подвержено прираще­ниям &iJ от одного промежутка времени г к другому, а эти прира­щения являются не А по отношению к AiJ и отрицают их. В резуль­тате Ai7 представляет приращение Л)/ за характерный промежуток времени Л так что накопление "ne&\J' за время т дает AiJ. т. е. Лг/ = т' d^\Jldt. Поскольку же Ai/ само является "неА " по отношению к 4, то Дз/ является уже "неА". т. е. отрицанием отрицания .4, что символизирутся d/dl(dJi/dl) = .d^Ji/dl¹, так что АгУ = t't d^lJ|/dt^l = L <PJ,/dl¹, где L = t't.

Пользуясь терминологией теории автоматического управления, можно сказать, что процесс самоотражения образует два контура отрицательной обратной связи: один - по скорости (обозначен цифрой 1), другой по ускорению процесса (обозначен цифрой 2). которые замедляют процесс отражения, уменьшая в каждый момент времени актуальную информацию J^ по сравнению с потенциальной информацией У„, так что ^ = R„(J, - Ai7 - AiJ) = /^(/д - г dJ^dl -LfJi/dl²). В результате с учетом Jy = Mk имеем

М„ = 7k/R^+ г dJi/dt + L (PJi/dt¹. (3.105)

Это соотношение гносеологически символизирует процесс ста-човления информации (знания) как совокупности внешнего отраже­ния материи (первое слагаемое) и самоотражения (второе и третье ^агаемые), причем последние символизируют соответственно от-Рицание и отрицание отрицания информации.

Диалектико-логическое соотношение (3.105) символизирует син-^те3 знания как единство противоположностей, тезиса Ji/Rk и анти-^иса rdJi/dt, .опосредованных переходным членом L^PJi/dt¹.

223

Наконец, математически это дифференциальное уравнение вто­рого порядка, связывающее информацию и материю и позволяющее оперировать количествами того и другого. Последнее стало воз­можным, поскольку описав вначале чисто символически посред­ством структурной схемы процессы отражения, мы указали способ измерения в каждых конкретных условиях, скрывающихся за сим­волами Mfc и .4 материи и информации.

Тем не менее (3.105) может использоваться и для чисто каче­ственного, содержательного описания диалектики отражения, по­скольку в соответствии с вышеизложенным эта символика может интерпретироваться и в естественном языке; материя в каждый мо­мент ( отражения выступает как совокупность потенциально усво­енной информации (ji/r^), его накопившегося за г отрицания df при отрицании dt постоянства времени и накопившегося за L отри­цания отрицания при тех же условиях.

В этом изречении материя вполне может быть заменена потен­циальной информацией J,. или, что то же самое, абсолютной исти­ной, имея в виду, что актуальная информация J^ является относи­тельной истиной. Однако это качественное описание не позволяет исследовать всякого рода тонкие эффекты, нюансы, доступные лишь строгому количественному анализу.

Так, решение (3.105) как математического уравнения позволяет исследовать характер процесса становления знания в зависимости от соотношения пара­метров Rk, т и L орга- J | нов чувств. При этом. если R^f > 4L, то процесс носит посте­пенный плавный ха­рактер (кривая 1 на рис. 3.3), а если R^f' < 4L. то процесс носит колебательный харак­тер (кривая 2 на рис. 3.3) с частотой <а

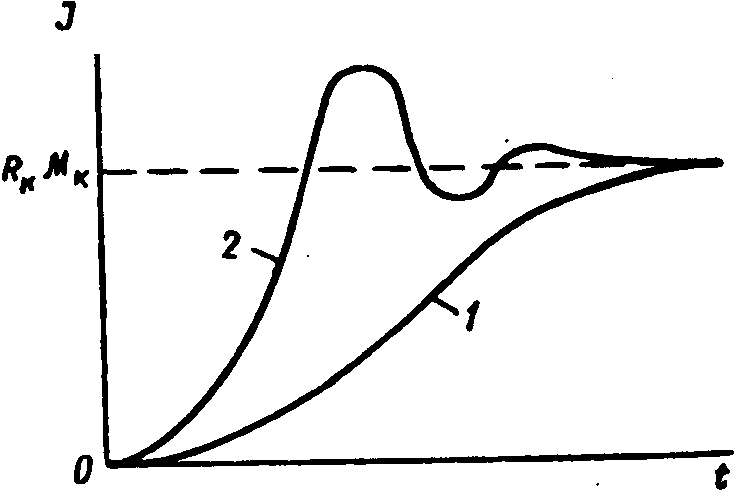
=^L/R„-T² /2L,

Рис. 3.3

которая имеет максимальное значение евши = (•ч LRt) '' при усло­вии, что г =0.

С другой стороны, эта точность описания может оказаться ил­люзией, если мы заранее не изучим влияние информации / и ее производных на параметры органов чувств, поскольку согласно диалектическому закону перехода количественных изменений в ка-

224

чественные следствием такого влияние может быть качественное изменение систем отражения, не поддающееся линейному описанию (3.105) ввиду непостоянства параметров/?t, г и L. Тщательное изу­чение органов чувств (человека или системы восприятия информа­ции предприятия) позволяет задать эти параметры как функции информации и ее производных, что превратит (3.105) в нелинейное уравнение, однако в этом случае его решения уже не будут сводить­ся к изображенным на рис. 3.3 кривым, да и сами решения не всегда могут быть получены аналитически. Таким образом, наиболее эф­фективен при изучении процессов отражения синтез диалектик” и математики, при котором всегда справедливая качественная трак­товка (3.105). обладающая достоинством всеобщности, сопровож­дается количественным уточнением нюансов посредством матема­тического решения (3.105) для конкретных, особенных условий от­ражения.

В свете сказанного становится необходимым проследить пути формирования на основе единого продукта чувственного отраже­ния столь различных категорий, как количество и качество.

Попробуем пояснить графически различие между бинарной и диалектической логикой.

Допустим, мы располагаем некоторой шкалой истинности суж­дений, помещенных на оси ординат (рис. 3.4). По оси абсцисс от­кладывается время. Мате­матическая логика признает только два состояния по шкале истинности для лю­бого суждения - либо ис­тинно - обозначаемое еди­ницей, либо ложно, обозна­чаемое нулем. В отличие от нее диалектическая логика использует всю шкалу меж­ду 0 и 1, причем допускает сколь угодно малые шаги по этой шкале.

Рис. 3.4

В частности, относительно истинное суждение диалектической логики может в своем развитии последовательно проходить, на­пример, состояния а. Ь. с, каждое из которых не истина и не ложь в смысле бинарной логики. Если исходным является суждение а, то согласно закону изменчивости (отрицания) через некоторое время оно разовьется в суждение Ь, а затем согласно закону отрицания °трицания в с, как показано на рис. 3.4.

В бинарной логике, если начальным было состояние 0, но уда­лось доказать, что на самом деле 1, то отрицание нуля в какой-то момент приведет к скачкообразному переходу в состояние 1, как показано прерывистой линией. Но если потом доказано, что 1 быть

225

не может, то отрицание отрицания нуля вновь приведет к скачку в О и т. д. без конца, если суждение парадоксально.

Это и происходит, например, в парадоксе лжеца: нельзя дать положительного ответа на вопрос "Ты лжешь?", ибо если ответ "То, что я говорю - ложь" правда, то отвечающий солгал, а если это ложь, то отвечающий произнес истину.

Диалектическая логика не может оказаться в такой ситуации, поскольку для нее все истины относительны: "То, что я говорю, - в какой-то мере ложь". Если я сказал в какой-то мере правду, то это справедливо: если же я в какой-то мере покривил душой, то это не менее справедливо.

Процесс становления логической информации Н может быть пояснен аналогично рассмотренному процессу становления чув­ственной информации J.

Как отмечалось, логическая информация Н есть в общем случае взвешенное среднее чувственных информации ^ об однородных в определенном отношении объектах (3.92). Наиболее простой и есте­ственной является линейная логика, соответствующая параметру усреднения у = 1 и приводящая к среднему арифметическому

Н = ^-У” = J/n.-= ^Jt. w ⁿ i-i

(3.106) где qk - вероятность встретить J^ среди всех л, объектов, N ”• число

Но

различных информации (объектов); J •= /J>.

i-l

Хотя (3.106) представляет собой математическую формулу для расчета логической информации, исходя из чувственных, информа­ции, она в то же время символизирует основной закон классической логики, согласно которому сущность Н понятия обратно пропор­циональна его объему Лд. Действительно, поскольку объем понятия есть число охватываемых понятием объектов, то чем с более общим понятием мы имеем дело, тем меньшей информацией Н мы распола­гаем о каждом из них.

Так, если любую конкретную вещь (л. = 1) разносторонне охарактеризовать не составляет труда, то о материи (л„ = ос), являющейся статистически средней вещью среди всех вещей, можно хкязать лишь. что она объективно реальна, т. е. существует. В последнем случае согласно (3.106). поскольку суммарная информация о существо­вании всех вещей составляет J = л„/^ при я, -” оо, где .4 - информация о факте существования одной вещи. Н = я, J^ л, = У”. Любое же другое свойство конкрет­ной веши. не присущее всем вообще вещам, при делении на л„ = <” неминуемо исчез­нет и для него применительно к материи Н = 0.

226

Применяя согласно (3.106) процедуру усреднения к (3.105), не­трудно получить

я”

М = ^ М / я. = Яд = H/Rk + г dH/dt + L (РН/dt¹, (3.107)

где Rk, т” L- средние значения соответствующих параметров кон­кретных органов чувств. Ну - среднее значение конкретной исти­ны Jo (потенциальной чувственной информации), имеющей статус всеобщей истины (потенциальной логической информации), т. е. универсальной в рамках всего объема понятия закономерности.

Если Mk обозначает, хотя и конкретное (данное непосредствен­но в ощущениях, чувственно), но любое материальное свойство, присущее хотя бы одному из объектов, охватываемых объемом л„ понятия, то М обозначает само понятие материального свойства, т. е. некоторую абстракцию, математическое ожидание конкретно­го свойства у объекта. Иными словами, если М^ та самая объек­тивная реальность, которая дана нам в ощущениях, то М - фило­софская категория для обозначения этой реальности, которая (категория) отнюдь не дана нам в ощущениях, а есть продукт логи­ческой переработки (усреднения) чувственных данных.

Впрочем, диалектика общего М и особенного М/с проявляется и в том, что они взаимно переходят друг в друга, например, когда измерения ведутся по принципу "да - нет" или "годен - не годен". В этом случае ад( = А„ все J^ равны единице, а их среднее значение Н = 7fc, так что М = М^, поскольку понятие о всех объектах из объема л„ сводится к констатации наличия у них общего свойства /^ вне зависимости от его количества.

С точки зрения учения об истине Нд как раз и есть истина бытия (абсолютная истина), которая согласно (3.107) даже с поправкой R,, на несовершенство органов чувств отнюдь не сводится к доступной нам в данных условиях сущности Н, являющейся относительной истиной, но требует согласно диалектике отражения также учета, во-первых, направления и величины г dH/dt, эволюции Н и, во-вторых, прогноза да­льнейшего развития |————| |———————————| //

LePH/dt², понятия. ^м ^.J ^/?*

Структурная иллю- '————* '—у————————f—\

страция диалектики логического отраже­ния приведена на рис. 3.5, который аналоги­чен рис. 3.2 и поэтому

не нуждается в допол- рис. 3.5 нительных коммента-

227

риях, если не считать того, что при чувственном отражении R^, т, т' характеризовали свойства органов чувств, a R^, т и г" здесь харак­теризуют интеллектуальные свойства субъекта.

Кроме того, согласно (3.106) в процессе логического отраже­ния в неявном виде участвует память субъекта, поскольку объем л понятия есть по сути число объектов, о которых помнит субъект в процессе формирования понятия о нем.

Процесс становления понятия, описываемый решением (3.107) как математического уравнения, аналогичен по своему характеру получению чувственной информации (см. рис. 3.3), и поэтому мы не будем на этом задерживаться. Здесь уместно отметить, что понятия не обязательно формируются на базе чувственной информации. Основой более общего понятия Н могут быть понятия Н^ менее общие, подвергаемые усреднению в соответствии с тем же (3.106), где вместо /^ подставляются Н^, а в качестве Яд используется об­щее число этих исходных понятий.

Подчеркнем, что в общем случае шенноновская энтропийная мера (3.906) не имеет никакого отношения к (3.92), и может быть сведена к (3.92) только, когда, во-первых, имеет место линейная (у = 1) логика (104); во-вторых, распределение показаний приборов подчиняется закону Пуассона (тогда J = - log2 р)', и в-третьих, ^ = pie. Выполнение всех трех условий можно встретить не столь часто, как может показаться, поэтому огульное использование (3.906) вне теории связи нередко приводит к неверному результату. В част­ности, например, в процессе гравитационного взаимодействия имеет место нелинейное (геометрическое у = 0) усреднение чув­ственных информации, и (3.906) там неприменимо.

Процесс формирования понятий сопровождается еще процес­сом установления всякого рода связей (например, причинно-следственных) между ними, поэтому помимо логики (3.92) усредне­ния должна быть еще логика связей типа

С=ЛД), (3.108)

где С - содержание Н с точки зрения некоторого другого, связанно­го с ним понятия. Соотношение (3.108) означает, что из Н посред­ством / следует С.

Например, уравнение у = а\х¹ + a-ix + аз путем квантования переменных посредством (3.81) приводится к виду

^аДх^а^^

Ду Ау

где С=у/&у, Н=х/Ах, Сд=аз/Ду. 228

Этот результат соответствует квадратичной логике связи между понятиями С и Н. В простейшем случае линейной логики

С = ПН + С„,

(3.109)

где П - содержание единицы Н, которое мы будем именовать по­тенциалом понятия Н с точки зрения понятия С, а С„ определяется значением С при Н = О.

Разумеется, мы можем оценивать содержание не только поня­тий, но и материи (материальных свойств), поэтому в частном слу­чае вместо Н в (3.108) и (3.109) может быть М. Например, по­скольку понятие С трехзначного числа включает троекратное ис­пользование понятия Н цифры, то С = 1/3 Н, а П = 1/3, ибо на еди­ницу Н приходится 1/3 С. Точно также, если энергия W = м, кон­денсатора определяется произведением его напряжения и и q, то, квантуя согласно (3.81) энергию и заряд, получим С = IJJ, где С = W/bW, J = q/Aq, П = u&q/^W. Здесь энергия определяет содержание его (заряда) единицы. Поскольку потенциал есть также логическая информация о цене J с точки зрения С, то как всякая логическая информация согласно (3.1 Об) она может быть выражена через объ­ем понятия п" и свою чувственную информацию J': П = JW, откуда согласно (3.108) С = J'J/n'.

Если же нас интересует содержание информации J относительно самой себя, то из (3.109) имеем С = Л/п, где л = л' и J = J'. Так, квантуя энергию и заряд в формуле для энергии конденсатора W = qVCy где Су - емкость последнего, получим л = Сд AW/Aq.

Оценка прагматической информации, т. е. смысла с точки зрения цели, полезности для ее достижения, может быть получена с исполь­зование тех же соотношений, что и оценка содержания, логической информации. Вместе с тем в некоторых случаях м содержание мож­но рассматривать как частный случай смысла на фоне познания природы без попыток утилизации знания. Иными словами, содер­жание имеет смысл познания, а смысл есть содержание применения, использования знания, т. е. содержания практики. В процессе по­знания содержание все время растет за счет увеличения точности приборов, способов получения информации, а смысл изменяется произвольным образом в зависимости от наших потребностей, ко­торые определяют ДЛ, причем, чем больше потребности, тем мень­ше ЛЛ, и наоборот.

Рассматривая примеры расчета содержания и смысла, мы имели в виду, что сами понятия уже сформировались и потому логика их взаимодействия носит стационарный характер. В действительности *е, представляют интерес содержание и смысл не столько понятий и ощущений J, сколько отражаемых ими объектов. Становление со-

229

держания и смысла в процессе отражения можно получить под­ставив (3.109) в (3.107):

М = C/URk + г dC/Udt + Ld^гC/Пdt\ (3.110) которое протекает аналогично становлению понятия (см. рис. 3.3) при тех же условиях, причем это соотношение также трактуется и количественно и качественно, т. е. в соответствии с диалектической логикой. В последнем случае оно означает, что содержание материи в любой момент времени определяется, во-первых, наличным (усво­енным) содержанием С, во-вторых его отрицанием в процессе отри­цания времени г dC/dt и, в-третьих, его отрицанием отрицания LcPC/dl¹. Более того, только с учетом всех этих компоненты материя тождественна своему содержанию и только через них и выступает как философская категория.

Учитывая особую роль цели в теории систем и системного ана­лиза, рассмотрим логику процесса достижения цели. Поскольку всякая вещь обретает смысл лишь на фоне целенаправленной дея­тельности, сама цель деятельности определяется через него как его предельное значение. Иными словами, если определить цель как отраженный экстремум функционала нашего существования, то в роли этого функционала как раз и выступает смысл. С учетом (3.108) это означает, что цель как экстремальное значение С тре­бует экстремальных значений Ли Я.

В частности, например, как можно больше промышленной продукции Н наибо­лее высокого качества П.

С этой точки зрения деятельность, практика представляют со­бой процесс активного, принудительного отражения целей челове­ка, общества в живой и неживой природе, среде обитания. Поэтому материальные продукты человеческой деятельности, как и всякие продукты отражения, также несут информацию о целях своего творца.

Однако по мере достижения цели смысл и потенциал средств ее достижения все время падает, так что целенаправленная деятель­ность подчиняется логике максимально возможного уменьшения потенциала

n=-gradC=-gradnAf=EA/, (3.111)

где Л - вектор логики движения в пространстве цели; Е = Л1М -напряженность поля этой логики.

Конечно, природа не обладает свободой воли, не ставит перед собой целей, однако она следует совершенно определенной объек­тивной логике, которая совпадает с (3.109). Действительно, квантуя выражения для электрической и механической сил, получим

awAwAW. и F-

„„_Е^А^

*€ - Ь”^ -

230

где Е, - напряженность электрического поля, а - ускорение, b.W -квант энергии, получим с учетом (3.81) Л = ЕМ.

Здесь в первом случае Л = F^W„ Е = E,Aq/A”^, а во вто­ром случае Л = FJ\W^ Е = a Am/A”„, причем Е= - grad Л, по­скольку Е,= - grad и и а = - grad Л„„ где и и Л„ - потенциалы соот­ветственно электрического и гравитационного полей.

Таким образом, наша субъективная логика и объективная логи­ка природы аналогичны, хотя природа не выбирает объектов для приложения своей логики, а мы делаем это по своему желанию.

Все же абсолютное противопоставление бинарной и диалекти­ческой логики было бы неверно, поскольку при дроблении объек­тов исследования эти виды логики могут переходить друг в друга.

Диалектика - это логика целостности, а бинарная логика - ло­гика частей, к которым можно свести систему при достаточно глу­боком дроблении объектов. Это значит, что главной причиной си­стемных представлений является стремление обойти сложную диа­лектику целого путем перехода к бинарной логике его частей. Но диалектическое суждение не есть сумма бинарно-логических сужде­ний, так что структуризация может привести к потере целостности.

Для ее сохранения и используются различные усреднения вос­принимаемой информации, отображаемые в соответствии с (3.92) в Н, и важным этапом при формировании моделей является выбор параметра усреднения у. Полученные в соответствии с выбранным у значения Н, в свою очередь, отражаются в оценке сложности си­стемы С. В результате из одинаковых элементов в различном соче­тании можно получить разную целостность, и, напротив, одинако­вые целостности могут быть получены из разных элементов (см. примеры в [2.4, с. 58-^60] и в гл. 7).

Рассмотрим теперь целостную модель проблемной ситуации, в которой отображены несколько материальных свойств или объек­тов с учетом их взаимного влияния друг на друга. Такие ситуации могут быть описаны соотношениями типа (3.88) или (3.97), а в слу­чае линейной аппроксимации - (3.89) или (3.98).

На основе соотношений типа (3.89), (3.98) можно ставить опти­мизационные задачи, преобразуя любое из входящих в них симво­лических уравнений в целевую функцию, а остальные - в ограниче­ния-неравенства.

Соотношения такого рода позволяют исследовать устойчивость проблемной ситуации или системы, описываемыми этими соотно­шениями, что можно делать, используя, например, критерии устой­чивости динамических систем типа Рауса-Гурвица, Найквиста, Ми­хайлова согласно которым, как известно, об устойчивости можно ^дить на основе определителя системы соотношений типа (3.89), (3.98); или критерии В.М.Попова, В.А.Якубовича, квадратичный, 231

1

круговой и др. критерии при выборе других усреднений, обра­щающих соотношения (3.88) и (3.97) в нелинейные системы диффе. ренциальных уравнений.

В отличие от теории автоматического управления, где рассмат­риваемые соотношения, как правило, полностью определены, при описании реальных ситуаций в соотношениях (3.88),ь (3.97) или по­лучаемых на их основе (3.89) и (3.98) могут быть известны не все параметры, либо отображаемые суждения могут быть противоре­чивыми, что требует разработки специальных методов решения таких уравнений (например, один из методов получения интерваль­ных решений, не полностью определенных уравнений предложен А.В.Бобрищевым [2.5]), или разработки специальных подходов или методик исследования рассматриваемых символических отображе­ний с использованием методов из групп МАИС и МФПС.

Результаты решения систем уравнений (3.89) или (3.98) могут иметь такой же характер, как решения отдельных уравнений, типа приведенных на рис. 3.4. Особый интерес представляют ситуации, для которых решения имеют вид типа кривой 2 на рис. 3.4. По­скольку в зависимости от соотношения параметров л, г и L решения могут носить не затухающий характер, а амплитуда колебаний мо­жет возрастать. Такой характер решения свидетельствует, с одной стороны, о неустойчивости системы, но, с другой стороны, такие ситуации могут служить основой развития, что свидетельствует о наличии негэнтропийных тенденций в системе, источники которых нужно выявлять, исследовать и управлять ими для создания ситуа­ций управляемого, устойчивого развития системы.

С учетом рассмотренного информационный подход к анализу систем имеет широкий спектр приложений, позволяет получать оценки структур, свертку разнородных критериев при решении многокритериальных задач, разрабатывать методы организации сложных экспертиз, оценивать переходные процессы принятия ре­шений, тенденции развития систем различной физической природы и т. д. С примерами приложений подхода можно познакомиться в [8, 9, 3.1-3.5 и др.] и в последующих главах.

232