3.2. Дискретные информационные модели

Система как дискретная модель непрерывного бытия. Хотя системные исследования привлекли особое внимание специалистов различных областей знаний лишь во второй половине нашего века, нельзя сказать, что системность была открыта в эти годы. Дело в том, что теория систем взялась изучать древнюю, как мир, пробле­му взаимодействия части и целого, диалектику этого взаимодей­ствия, которую не обходила вниманием ни одна философская кон­цепция.

Это обстоятельство породило даже некоторую конкуренцию на ниве системоло-гии между профессиональными философами и представителями специальных наук. Первые (по крайней мере, некоторые из них) были склонны отрицать систсмологию как самостоятельную науку, поскольку-де она занимается философской проблемой (философия во все времена играла роль науки наук, обеспечивая их интеграцию и сохранение целосгности), либо отлучать ее от философии, поскольку системология прибегает к использованию математического аппарата, якобы чуждого философии. И, напротив, некоторые сисгсмологи стали претендовать на то, что теория систем является неким философским откровением и даже способна заменить собой тради­ционные философские системы.

Признавая, что математизация придает системологии особый статус, нельзя игнорировать во-первых тот факт, что системология занимается не какой-то общенаучной, а философской проблемой, изучая структуру отражения материи в нашем сознании, и, во-вторых, эта особенность, по-видимому, преходяща, поскольку раньше или позже и другие разделы философии будут вооружены математикой с целью придания им действенности и привязки к кон-'фетной социальной практике.

189

^^ гл. 1, понятие системы применительно к наши Как следУ д ^целом или об отдельных аспектах бытия подт)" знаниям о миг ^^окупность частей, элементов, дисциплин, Havi, зумевает неку' ^- . д., отражающих отдельные стороны бытия, ц точек зрения ^и взаимодействующих таким образом, что в р” взаимосвязан^ ^тируют целостность, присущую объективной ре. зультате они -у^ • они отражают.

альности, '"^„язо^' ^{система} - ^это категория отражения, форма

Таким ov' ^д-^ерии доступными пониманию средствами. Что представлении ^^льности, природы, то она континуальна, непре. касается сам^_ т. е. не содержит каких бы то ни было априорно рывна и U®¹¹⁰^,”!, которые мы выделяем в ней по собственному заданных ча^ _<обства изучения или представления, и которые произволу •^'.еч^ются в природе в отрыве друг от друга.

никогда не в^¹

^^ .птицу в небе, мы произвольно сосредоточиваем на ней свое

Так. разгл^^^уд^ь от того обстоятельства, что птица невозможна вне воздуд. внимание, абст^^^" доставляет с ним неразрывное целое, а голова птицы, крыщд,

ного пространс^щссп^^¹" ^сам" "° ^{себе и даже} П'²*™^¹ перехода друг в друга уст” лапы, хвост не ^„о Д,.^{3 BC}W^ птица и не "собирается" из этих частей, весь ее орга. довить невозмо<„ „ д^”родышевой яйцеклетке, так и остался един в своем развила низм как был е/*". (-ъДнако особенности человеческой логики, которая не толыю до взрослой ос^ „ fie^'P¹¹®^{1 He} позволяют понять континуальное целое, не разбив дискретна, но “^ уста^*⁰"^{116 те или иные} логические (функциональные) отношения его на части и ^-.„уводит к выделению тех или иных органов птицы и изучению между ними, ч^ их функций.

есто ^^{нтлакут} материальные продукты человеческого

Особое ^г рриборы, технические комплексы, которые соби-труда - '"'^'алей^ У^злoв и т. д., изготовленных отдельно и какое-раются из ту уло\щл\ вне связи друг с другом. Эти машины пред-то время ^^—у д^стемы деталей и узлов, поскольку являются про­ставляют ^у' дознания и воплощают в себе способ нашего отра-дуктом """^нос'*"^ объективной реальности в осуществлении тех жения в⁰³"^.,!!!!”!' ^т- ^е- воплощают нашу же дискретную логику.

или иных ФУ^-рязс””¹¹' материальные продукты сознательной челове-

Таким о „.„о^ти, с одной стороны, - системы, если иметь в ческой Д^^^ьнс” воплощенную в них логику функционирования, виду сознав д^оны, они континуальная целостность, если рас-но, с ДРУ¹'⁰^ дд<ологически вне связи с представлениями их соз-сматривать ^и дателей. —ема ~ ^{эт0 cпoco}б воспроизведения и отражения кон-

Итак, с^ д^сности средствами нашего сознания, нашей лрги-тинуальной „д^ми, система - это дискретная модель непрерыв­ки. Другим”* ного бытия- ^одель, система может быть: физической моделью.

Как и в^ „„.n^ffmo (по данным наших органов чувств и измер-' когда она ^w ^\ ((одобна моделируемому объекту; либо логической тельных ср^"

190

числе математической) моделью, когда ее логика подобна (^в g моделируемого объекта; либо, наконец, имитационной (праг-^л0 ической) моделью, когда только ее целостное поведение (выход) ^алогично моделируемому объекта. ³ Имитационные системы являются обычно частными моделями,

претендующими на адекватность исходному объекту во всех ^не дшениях. Физические и логические модели, напротив, претен-°„уг на адекватность отражения исходного объекта как в целом, ,v и в деталях, и даже приписывают свою системную структуру “оделируемому объекту, что является распространенным заблужде­нием.

В то же время необходимо еще раз подчеркнуть, что если мы выделяем в орга­низме те или иные органы, то только ради удобства изучения соответствующих функций, заведомо упрощая истинное положение дел. И, строго говоря, любая мо­дель является имитационной, поскольку принципиально отражает не абсолютно все элементы объекта, представляемого в виде системы, а лишь те, которые помогут понять изучаемые особенности, в противном случае модель стала бы необозримой по размерности.

Иными словами, система - это еще и диалектический синтез вза­имно исключающих друг друга требований точности и обозримос­ти, а задачей прикладной системологии и системного анализа яв­ляется выработка средств достижения компромисса между "про­клятием размерности" и высокой точностью системного моделиро­вания актуальных задач практической деятельности человека.

С учетом вышесказанного ниже излагаются основные понятия информационно­го подхода применительно к системам с дискретно выделяемыми элементами, кото­рые выводятся из символического представления законов диалектики и диалекти­ческой логики.

Основные понятия дискретных информационных моделей. В гно­сеологии для отображения зсех способов получения информации принят обобщающий термин "отражение", а для обозначения всех первичных источников информации, образующих существующую вне нас объективную реальность, принят обобщающий термин "материя". Таким образом, вместо перечисления всевозможных источников информации и способов ее добывания из них можно просто говорить об отражении материального мира (материи) в нашем сознании, которое всегда происходит с помощью наших ор­ганов чувств, т. е. зрения, слуха, обоняния, осязания, вкуса (или технических дополнений - измерительных приборов, увеличи­вающих разрешающую способность органов чувств и доступных источников информации).

Согласно формуле познания "От живого созерцания к абстракт-""му мышлению, и от него - к практике"' можно выделить три

^в И.Ленин. Философские тетради. - Поли. собр. соч. - Т. 29. - С. 153.

191

этапа отражения действительности: два пассивных - чувственное логическое отражение, и один активный - этап прагматическо? отражения.

Соответственно продуктами этих этапов являются чувственная логическая и прагматическая информация.

Чувственная информация J вводится как мера отраженной в на­шем сознании элементной базы системы в форме

(3.81)

где А - общее количество каких-либо знаков, воспринимаемых из­мерительными приборами или нашими органами чувств, Д^ "квант", с точностью до которого нас интересует воспринимаемая информация, или разрешающая способность прибора.

Здесь необходимо пояснить принципиальное различие между л и J. Если А всегда принято выражать числом, которое является классическим математическим объектом и в силу этого удовлетво­ряет закону тождества А = А. то об информации этого сказать нельзя.

Действительно, во-первых, / существенно зависит от разрешающей способ­ности выбранного измерительного прибора и определяется значимостью для нас измеряемой величины, т. е. целью измерений (хотя измеряемая величина от цели измерений не зависит). Так, наличие или отсутствие личного автомобиля у конкрет­ного гражданина фиксируется с точностью до ДЛ = 1 автомобиль, поскольку это обстоятельство для автолюбителя является весьма существенным. Напротив, свод­ные данные по производству автомобилей в стране приводятся с точностью до Д4 = 10 000 автомобилей, поскольку меньшее число автомобилей для страны в целом несущественно. Стало быть, если в большой стране производится 5 автомобилей в год, то информация о том, что пятеро ее граждан ежегодно становятся автомобилис­тами, составляет 5 бит, в то время как государственная статистика скорее всего констатирует, что автомобильная промышленность в стране отсутствует.

Таким образом, в прагматическом аспекте информация всегда несет в себе весьма значительный элемент субъективности и раз­лична для разных людей при одном и том же А . Во-вторых, даже при фиксированном &А информация, строго говоря, не является числом, поскольку в пределах более или менее ограниченных А^ она может иметь любое значение.

Так, если вольтметр с разрешающей способностью в I В показывает 200 В, то истинное значение напряжения скорее всего лежит либо в диапазоне от 200 до 201 и' либо в диапазоне от 199 до 200 В-, причем в общем случае оба диапазона равное^ роятны, так что можно ввести логарифмическую меру единицы информации А-- log; р = logz 0,5 = 1 бит, где р - вероятность наличия или отсутствия минимально­го значения информации. Таким образом, с учетом соотношения (3.81) показан!” вольтметра дают нам J = 200 + 1 бит информации, откуда следует, что информант не число, а величина, размытая в пределах 1 бита. Это значит, что в семантическо аспекте информация всегда есть J. Но в то же время, и в том же отношения она н

192

т е. не удовлетворяет логическому закону тождества и несет в себе, хотя ес^ •ияную. ч⁰ относительную истину, в то время как число всегда несет в себе и '^''"'.ную истину. Так, показания вольтметра есть 200 В. когда стрелка остаиови-дбсолк”"^ делении шкалы, но в то же время не 200 В. так как показания прибора

^РИ⁶""™-

Г другой стороны, два или несколько одинаковых измеритель-прибора при измерении одной и той же величины в рамках их ^решающей способности могут дать различную информацию, но ^одинаковой достоверностью. Это значит, что информация не удо­влетворяет логическому закону исключенного третьего, не допус-яющему существование нескольких противоречивых, но одинако­во истинных величин, но зато удовлетворяет диалектическому за­кону единства и борьбы противоположностей.

Итак, информация - это понятие, не поддающееся анализу средствами формальной логики и требующее применения к нему диалектической логики, которая обеспечивает возможность анали­за не только абсолютно, но и относительно истинных высказыва­ний. С этой точки зрения J аналогична высказываниям естественно­го языка, которые всегда носят размытый и относительно истинный характер. Однако, ввиду дуальной природы J (число и не число) информация в отличие от вербальных форм поддается некоторым (не всем) математическим операциям.

Логическая информация (сущность) Н в отличие от J, всегда от­носящейся к конкретным объектам, или свойствам, характеризует целый класс однородных в определенном отношении объектов или свойств, являясь семантическим синтезом законов логики, правил функционирования системы и ее элементов, образующих функцио­нал ее существования.

Согласно основному закону классической логики Аристотеля собственная сущность (суть) системы обратно объему понятия л о

ней, т. е.

H-=Jfn^\. (3.82)

Объем понятия зависит от аспекта рассмотрения системы (эле­мента) и обычно предполагает родовую их принадлежность.

Например, объемом понятия "производственное предприятие" является общее количество вообще всех производственных пред-"риятий в городе (области, стране), а объем понятия "это произвол-ценное предприятие" равен единице.

Если речь идет о собственной сущности 100 рабочих предприятия, где трудится ^wv Рабочих, то согласно соотношению (3.82) ./=Z.4. где .4 - информация о "Чом рабочем, я = 3000, Н = 7^, где Jy - информация о среднем рабочем.

опосредования (усреднения) / может быть и иным (см. табл. 3.1).

193

Если система характеризуется множеством своих состояний, подобно pafv, неделе, которая состоит из понедельника, вторннха. среды и т. д., то это множес⁴? и составляет объем понятия "неделя" который равен я = 7. а сущность трех ^

и составляет недели Н = 3/7.

Отметим, что как вербальная форма основного закона логики так и символическая форма (3.82), являются размытыми, поскольку под обратной зависимостью подразумеваются различные конкрет ные формы, а соотношение (3.82), хотя и имеет форму обратной пропорциональности, но в силу размытости J также означает опре­деленный диапазон конкретных зависимостей. Вообще же количе­ственные значения Н и J в статике совпадают, (так как л = 1), од. нако в отличие от J, сущность понятия И не может быть объектом непосредственно чувственного восприятия, а является результатом логического осмысления, что отражается в трактовке п.

В частности, н можно рассматривать и как объем (емкость) памяти, занятой све­дениями об отражаемом понятии, поскольку понятие формируется на основе сведе­ний, содержащихся в нашей памяти (или в памяти ЭВМ).

Обратим также внимание на тот факт, что рассматриваемый закон в основе своей непрерывен (в силу обратной пропорциональ­ности л) и его действие должно распространяться на непрерывную (многозначную) логику.

Далее, конструируя сущность понятия Н, учтем в его символи­ческом представлении последовательно требования, предъявляемые законами диалектики применительно к суждению.

Первым в числе этих законов применим закон всеобщей взаимо­связи и взаимозависимости явлений. Чтобы учесть требования этого закона, следует дополнить соотношение (3.82) составляющими, отражающими взаимодействие исходного понятия с другими поня­тиями, входящими в систему, введя соответствующие обозначения для того, чтобы отличить эти составляющие друг от друга. Тогда

Н” =Л^А„ ^А/, ^2. - ^ -), (3.82Д)

где Hni - системная суть понятия; первый индекс при символ” означает номер понятия, учитываемого при отображении системы, а второй индекс - номер понятия, с которым взаимодействует дая-ное, так что Пц означает собственный объем i'-го.лонятия, а л,у - в³²" имный объем 1-го иу-го понятий.

Полученное соотношение (3.82д) соответствует обычному прэ виду формальной логики, согласно которому в любом определении Н^, должно присутствовать, во-первых, его родовая принадлв*" ность J\, а, во-вторых, видовые отличия Ji, Уз и т. д.

Следующим учтем требование, вытекающее из закона измен⁴"' вости ("все течет; все изменяется"). Поскольку, как показано вьив ' информация отражает относительную истину, она может изменять'

194

процессе познания и практики. Чтобы описать процесс ста-^сяв дня понятия, введем символ (оператор) d/dt, где числитель ^н0 ячает частичное изменение, а знаменатель указывает, что это ⁰¹ енение происходит во времени, так что, например, dJ/dt означа-^нэ изменение информации во времени. При этом накопление или йывание информации можно отразить знаками "+" и "-" соот­ветственно.

Отметим, что поскольку всякое изменение отрицает стабильность, т. е. ранее доменное, то закон изменчивости с равным основанием мог бы быть нйзван зако-"ц” awfWWW причем символ d/dt есть синоним частичного отрицания и соответ­ствует словесному "в каков-то мере не").

С учетом рассматриваемого закона сущность Нт процесса из­менения (эволюции) понятия должна быть обратно пропорцио­нальна уже не объему понятия л, а изменению этого объема понятия dn/dt= 1/г, так что

Hr=TdJ/dt. (3.83)

В дальнейшем г именуется информационным сопротивлением и характеризует как бы задержку при восприятии новой информации в процессе становления и эволюции понятия.

Здесь также можно учесть закон всеобщей взаимосвязи и вза­имозависимости и преобразовать соотношение (3.83) к виду

Я„ =Д% dJ/dt, т., dJ,/dt, Гу dJs/dl,..., Гу dJ/dt,...). (3.83а)

где //„ - системная суть эволюции <-го понятия; Тц - собственное информационное сопротивление; г;у - взаимное информационное сопротивление 1-го и у-го понятий.

Перейдем теперь к требованиям, вытекающим из закона отри­цания отрицания. Поскольку уже отмечалось, что закон изменчи­вости является по своей сути законом отрицания, то закон отрица­ния отрицания следует трактовать ка.ч двукратное применение за­кона изменчивости, т. е, как применение закона изменчивости к самому закону изменчивости. С формально-символической точки зрения это означаеп применение оператора d/dt к самому оператору ^wt, т. е. d(d/dt)/dt или d^/dt¹, так что, например, d²J/dl^I означает изменение эволюции информации во времени.

Сущность Н^ изменения эволюции понятия должна быть в этом •^учае обратно пропорциональна изменению эволюции объема "овятия y/dft = 1/L, так что

hl = L fJ/dft, (3.84)

^де I- будем именовать ригидностью (негибкостью) понятия, со­противляемостью изменению.

1

195

С учетом закона всеобщей взаимосвязи и взаимозависимо явлений соотношение (3.84) следует переписать в форме, аналоги^ ной соотношениям (3.82а) и (3.83а), т. е. ^11-

Ни =AL, dV/Л², L„ oV,/a(², L„ fWt¹,...,^ flV/A²,.;.). (з.щ

где На - системная суть изменения эволюции понятия; L„ - ул ственная ригидность данного понятия; Ly - взаимная ригидность i го и у-го понятий.

Закон отрицают мог бы быть применен еще раз, т. е. к закону отрицания дд цания, что привело бы к закону отрицания отрицания отрицания, символщесд" отображаемому fJ/dfi. Можно было бы говорить и о дальнейшем применении эако. на отрицания. Однако, повидимому, диалектика не напрасно не содержит законш тройного и более отрицаний, поскольку это было бы слишком громоздко и обреж нитсяьно для мышления. Наше мышление действует экономно, и все явления, вьвп. дящие за рамки закона отрицания, разбивает на транзитивные формы /^;=l(<p//((|;

//ц= 1л c^J/dft и т. д.. которые в совокупности передают сколь угодно сложные процессы.

Следующий закон диалектики, требования которого нужно учесть, - это закон единства противоположностей. Противопо­ложностями в нашем случае являются момент относительной ста­бильности понятия, соотношение (3.82а) - тезис, момент относи­тельной изменчивости (3.83а) - антитезис, опосредованные отрица­нием отрицания (3.84я), которые в соответствии с применяемым законом следует рассматривать в неразрывном единстве

H^-HnUHr^HL. (3.85) а в частном случае, если возможна линейная аппроксимация

Я=Н,,+Я,+/4. (3.86)

В более общем случае с учетом закона всеобщей взаимосвязи и взаимозависимости Я„, Нт и Н^ определяются согласно соотно­шениям (3.82а), (3.83а) и (3.84а), и тогда

Н, =Л//л„, т„ dJ,fdt, L,, (pj, ldt\

/,/д,„ т„ dJi/dt, L,, d^lJ^ /dfl, (3.8ВД JJn„, т„ dJitdt, L„ eV2/a(²,..., J^/ny, гу dJ^ldt, Lg fJ]ldft,...).

Это значит, что истинная суть Н объективной реальности слага­ется в каждый момент времени из сформировавшегося к этому "°" менту содержимого памяти //„ (отраженной сути); из той логиче-ческой информации //р которая пребывает в процессе перед”⁴" органов чувств к памяти; и из той логической информации m усвоению которой препятствуют привычки и предрассудки. По^ 196

что две последние составляющие преходящи, поэтому в конце ^н иов (при г = оо) они исчезают, оставляя в памяти адекватное """ческое отражение объективной реальности Н = Нд. ^я0 Но при всей универсальности формы (3.85) она не конструк-

ана поскольку не указан способ ее построения из имеющихся ^(Ьормаций. Однако размытость (3.85), символизирующая не ^и "цик), а размытую область, в которую укладываются многие —ции, позволяет аппроксимировать ее участками размытых ли­нейных зависимостей в форме

Н = J\/nt + n dJt/dt + Li dVi/ai² +

Ji/пт. + Г2 dJt/dt + Lz dVz/A² +... + (3.87) /A + г, dJ/dt +L,d²Ji/a^² +...

Соотношение (3.87), хотя столь же размыто, как и выражение (3.86), имеет стандартную для всех приложений форму, все компо­ненты которой могут быть рассчитаны с учетом реальных условий, определяющих константы Пц т, и l(-

С учетом закона всеобщей взаимосвязи и взаимозависимости получим систему соотношений

№ =fiJx/nn, r,i dJi/dt, Ln dVi/ift², jt/п^ m dJVdt, Ln d^Ji/dt\...\ Hi =M/"”, ^i dJi/dt, £21 (PJt/dt¹, /2^22, Г22 dJt/dt, Ln d¹^^,...), Н, =A-f/^, .„ dJ/dt, L,, (PJ/dft, J/ny, Ту dJ/dt, Ly (PJ/dft,...), (3.88)

Я„ =AJ^„ ^ dJ,/dt, L^i fJ./dfl, J^, r^ dJ^dt, L^ (PJVdft, -, J^n”, ^ dJ^/dt, L^, d^J^dft,...),

или в случае линейной аппроксимации и некоторых перестановок составляющих, что удобнее для ряда приложений, получим

H^=J^/nn•^-J^/nn+...+тndJ|/dt+т^ldJ]/dt+L^^d^lJ^/dt²+Lnd^гJ]/dt^l+,...,

Hi = ]\/щ i ^-Ji/ii-а +... + Т21 dJ\/dt + mdJi/dt +Li i dVi/<ft² ^^J^d^ +,...,

(3.89)

Н, = J/n„+J/ny+... +Ti^J/dt+т,/^J/dt-^•L„•dⁱJ/dt'^t-^-L,^d^lJ/dt'^г+,...,

H^=J^,+J]/n^+...+J^, +r^rf/,/A+r„^2/A+...+r^, dJ^/dt+ +L^(PJ,/dt^L^J2/dt^+...+L^ (PJ^dft

Система размытых относительно истинных (диалектических) ^t;У*дeний типа (3.89) позволяет сделать символическое размытое Умозаключение путем решения этой системы по правилам, отли­чающимся от математических в той мере, в какой диалектическая lormca отличается от классической, т. е. в меру влияния законов то­ждества исключенного третьего. Отсутствие этих законов классиче-

197

ской логики, т. ^у. фактическая замена их законом единства дрот воположностей, -приводит к тому, что, с одной стороны, в отдич¹¹ от математики суждения типа (3.87) всегда совместны, ибо, разщ⁶ вая область их существования, всегда можно их частично совц“г тить, а, с другой стороны, линейные комбинации этих суждений и являются тавтологиями, ибо в силу размытости не вполне сводя ^е друг к другу.

В частных случаях (что определяется на этапе обоснования мо­дели конкретной проблемной ситуации) соотношение (3.87) мо”ег рассматриваться как обычное дифференциальное уравнение, а си­стема уравнений; (3.89) может решаться в соответствии с принятой в математике процедурой преобразования и решения дифференци. альных уравнений, учитывающей логический закон достаточного основания (в соответствии с которым число суждений должно быть не меньше числа объектов, о которых должно быть получено умо. заключение), логические законы противоречия (требующий непро­тиворечивости, совместимости суждений) и тождества (требу­ющий изобража-гь синонимы одним и тем же символом).

Названные логические законы полезно учитывать и в более об­щих ситуациях применения соотношений (3.89). При этом следует иметь в виду, 4-го отмеченные отличия диалектической логики от классической являются глубоко принципиальными и приводят к неоднозначности”, множественности умозаключений на основе од­ной и той же си<^гемы суждений. Это позволяет, в частности, поста­вить вопрос о выборе среди них наилучшего управленческого или проектного рец^ения, т. е. сформулировать задачу оптимизации, которая в этой постановке сводится к поиску такого решения си­стемы соотношений типа (3.89), в котором выбранная в качестве критерия оптимальности некая комбинация из \А, была бы мини­мальной. Это означает, по существу, поиск наименее размытого решения система из всех возможных.

Наконец, щоеледний закон диалектики, подлежащий учету, -закон перехода количественных изменений в коренные качественны - требует понимания того, что характеристические константы я, f и L являются константами лишь в ограниченном диапазоне эволю­ционных изменении понятия. В общем же случае, т. е. при большю изменениях, зтм константы могут не сохранять своих значений, что приведет к радэдсальному (революционному) изменению сути по№ тия, нарушив плавный эволюционный ход развития. С формальной точки зрения э-то означает, что в общем случае л, г и L являютс” функциями Н, V. dJ/dt, oV/A².

Отметим, чего хотя параметры л, г и L названы выше соответ^ ственно емкостью (объемом памяти), информационным сопроти'' лением и ригид.востыо понятия, но поскольку последнее формируй'

198

сознании одного человека (или в перспективе - в памяти кон-°*^„oh системы восприятия и хранения информации с использова-^ ЭВМ)” ^{т0 эти} параметры, по существу, характеризуют память, "опускнУ¹⁰ саособнос-гь ^и ригидность психики конкретного чело-"• (или автоматизированной информационной системы) и могут быть измерены экспериментально, что следует периодически по-торять с учетом последнего из рассмотренных законов.

Если периодически уточнять л, г и L, то выражение (3.87) бу­дет сохранять неограниченную универсальность при описании лю­бых явлений; причем, описывая сложное явление поэлементно, оно сохраняет целостность, присущую соотношению (3.86).

Логическую информацию Н можно определить не только через параметры синтезирующей ее системы (человека, автоматизирован­ной информационной системы). Если учесть, что, как было отмече­но выше, Н характеризует, не единичный объект, а класс одно­родных в определенном смысле объектов или свойств, то Н можно определить через плотность вероятности ДУ,) того, что J имеет зна­чение J,

(3.90)

В частном случае вместо плотности вероятности можно охарак­теризовать класс однородных объектов просто вероятностью q, и представить J, в логарифмической форме; тогда получим

(3.90fl)

H=-^q<\ogp,.

1-1

Значения q, и p^ могут быть не равны, но возможны ситуации, когда q, = p„ что имеет место в формуле Шеннона

(3.906)

<=1

Прагматическая (целевая) информация Я, описывается моде­лью, аналогичной (3.86), только под J понимается информация о Федствах достижения цели, а под л - количество бит информации о федствах на бит информации о цели (результате).

Прагматическая информация Я„, так же, как и рассмотренная ”ыще семантическая Н, может иметь и статистическую трактовку, ^т-^е- Н^ может определяться аналогично (3.90fl), только в этом слу-^тае для практических приложений часто удобнее заменить вероят­ность недостижения цели р, на сопряженную (1 -р,')

(3.91)

H=-^q.\^(\-p!).

1=1

199

где р,' - вероятность достижения цели; q, - вероятность того, что^ оцениваемая компонента будет использована для /достижения цепи.

Таким образом, из вышесказанного следует, ^что J н И могут, измеряться различными способами - детермин^Р⁰^^{11110 и с} по^

мощью вероятностных характеристик.

При детерминированном измерении можно прч^ть Р^-чичнук^

форму усреднения (опосредования), для чего вво.дчтся параметр у,, который может выбирать постановщик задачи. Тс?¹^

Я=г?-У^, (3.92) \п^

где J, - результаты измерения А, согласно (3.81); ft - объем понятия, т. е. число, охватываемых понятием объектов; у "" параметр логика усреднения, при различных значениях которого? получаются раз-,. личные выражения для определения Н, приведен^"® ^в табл. 3.1 ((g

таблице знак П - знак произведения).

Поскольку в некоторых приложениях могут ^ыть использована

одновременно обе формы представления инфор'**^¹*⁰¹¹¹¹¹'" харак­теристик - и детерминированная, и вероятности^' ^а также - пере--ход от одной формы к другой (см. примеры в rJ¹- ^” ^)> то удобнее пользоваться сопоставительной таблицей 3.1, в к^⁷¹'⁰?⁰" приводятсэя

основные способы измерения J н Н.

Следует оговорить особенности вероятности¹'⁰¹ характеристики, используемых в излагаемом подходе. В частно”* случае р, может быть статистической вероятностью, определяем^ на основе репре­зентативной выборки, подчиняющейся той юи” ^инои статистиче­ской закономерности. Однако в общем случае вероятность дости­жения цели pi' и вероятность использования оцениваемой компо­ненты (свойства) при принятии решения q, могут иметь более широ­кую трактовку и использоваться не в строгом C1лv^{l(яв с} точки зрении теории вероятностей, справедливой для стохаст”*⁴®⁰⁰"' повторяко-щихся явлений, а характеризовать единичные явления, события, появление которых нельзя предсказать на основ⁶ представительном) выборки. Иными словами, pi и q: - это вероятн^^тч' более близки" по смыслу вероятностям теории размытых множите Заде.

Добавим также, что по аналогии с предшес^вУ¹⁰""¹*¹¹¹ исследсо-ваниями Хартли. Шеннона, Харкевича, в качеств® единицы измере­ния информации принята единица, основанная ^на двоичном лог^ рифме, дающая в качестве минимальной едини^" информации в^ личину 1 бит. Это удобно и по следующим cooбf>^{я]кeflням}• Д™ ^то-чтобы (3.81) давало информацию в битах, неодолимо понимаШ. что априорная принадлежность каждого делеИ¹" шкалы измер”*

200

кого прибора измеряемой величине составляет 0,5. Тогда, по-^тель ^у шкала представляет последовательное соединение делений, ^ск местная вероятность того, что J из них принадлежат измеряе-ой величине с учетом (3.81) составляет р = 1 ~\ откуда получа--„ у= - \ogip, которая вместе с тем является решением уравнения

(3.93)

-^_\og2e+p=0. си

В то же время, в принципе могут быть приняты и иные меры сжатия информа-яонной шкалы - восьмеричные логарифмы - банты (уже нашедшие применение оценки объемов информации в вычислительной технике) или даже, не приме-щцощисся пока - десятичные логарифмы (единицу можно назвать, например, "дек"), напрасные логарифмы ("нат") и т. п.

Сложность (содержание, смысл) С определяется пересечением (логическим произведением, а в частных случаях - декартовым про­изведением) 7 и Я

C=JnH или C=Jx Н. (3.94)

Соотношение (3.94) введено выше при изложении теории информационного паяя, а для дискретного варианта может быть пояснено следующим образом: Н характеризует содержание (суть) только единицы чувственной информации, а для того, чтобы охарактеризовать сложность всей информации, нужно, естественно, умножить Н на количество чувственной информации /.

Для случая прагматической информации сложность С, (смысл информации для достижения поставленной цели) должна опреде­ляться с учетом прагматической чувственной информации, влияю­щей на достижение цели, и прагматической сути Н^ (3.91).

В физических системах С соответствует энергии. Для систем организационного управления интерпретация этого понятия зави­сит от конкретных условий его применения. В широком смысле С характеризует сложность разного рода.

В частности, в зависимости от того, применительно к харак­теристике всей системы или ее элементов используется С, можно говорить о системной, собственной и взаимной сложности.

Слагаемые J/nn, t„ dJ/dl, L„ (PJ/dt¹ каждого уравнения в соотно­шении (3.89) описывают собственную суть Но соответствующего элемента вне связи с остальными элементами системы, а остальные слагаемые описывают его взаимную суть Н„ т. е. суть взаимодей­ствия данного элемента со всеми остальными, так что системная суть

Я,=Яо+//,. (3.95)

Если учесть чувственную информацию J, то получим соотно-•чение, определяющее взаимосвязь системной С<, собственной Со и ^имной Св сложности системы

Сс = Со + С,. (3.96)

201.

1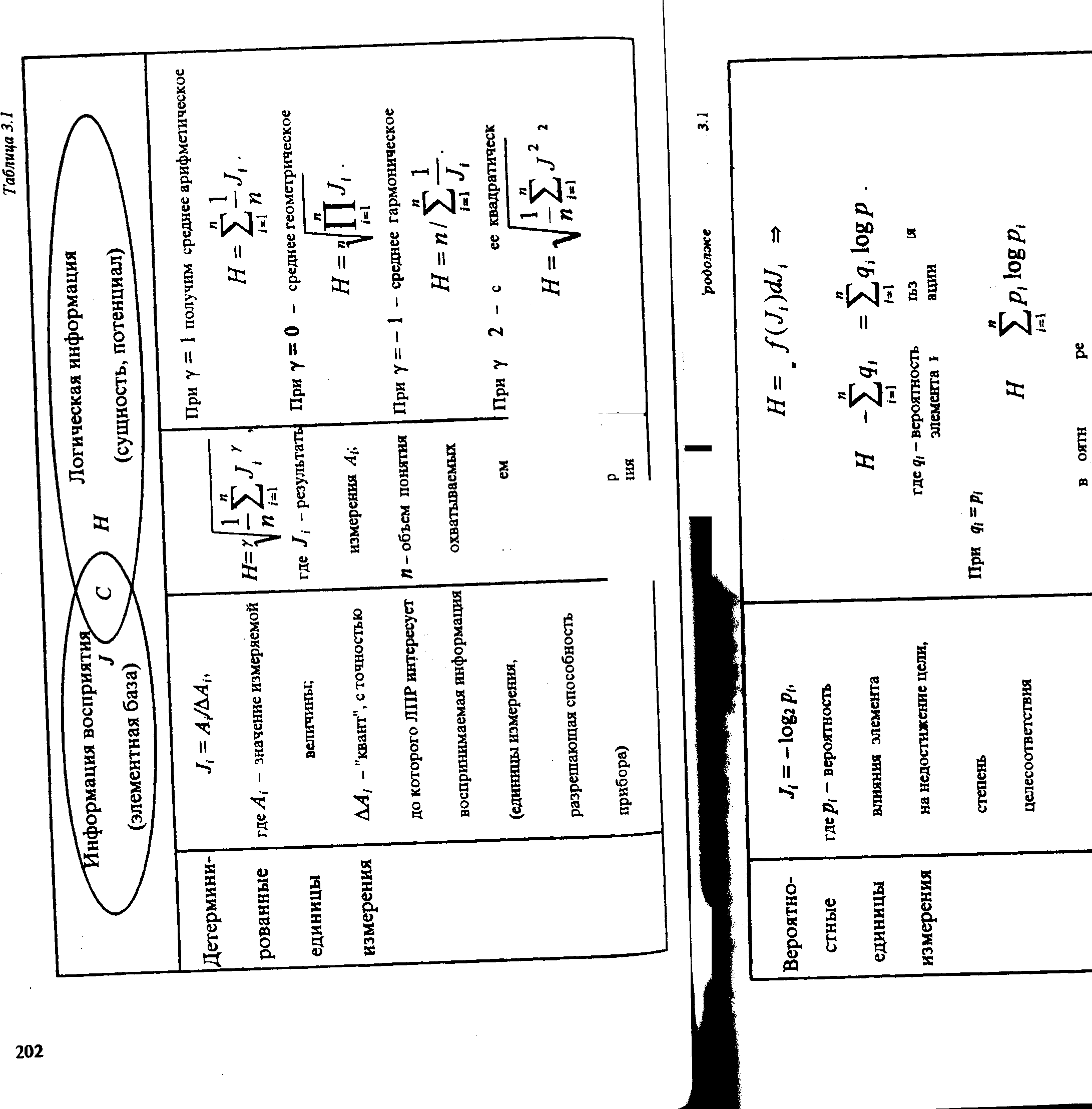

Собственная сложность Сс представляет собой суммарную сложность (содержание) элементов системы вне связи их между со­бой (в случае прагматической информации - суммарную сложность элементов, влияющих на достижение цели). Системная сложность Со представляет содержание системы как целого (например, слож­ность ее использования). Наконец, взаимная сложность Св харак­теризует степень взаимосвязи элементов в системе (т. е- сложность ее устройства, схемы, структуры).

Понятия системной Сс. собственной Со и взаимной Св сложности позволяют более глубоко осознать диалектику взаимодействия системы и ее частей. Учитывая важность этой проблемы, она вынесена в самостоятельный подраздел (см. более подробно ниже)

Для отображения сложных проблемных ситуаций могут быть получены соотношения, аналогичные (3.88) и (3.89), но учиты­вающие текущую J, для каждого из соотношений, описывающих динамику становления понятий, включенных в описание проблем­ной ситуации:

С, =А^/Пп, Гц 7,V7i/A, L„ ./i'yVi/(ft²,

./ь/2^12, П2 Ji'dJ^dt, Lu./i'tfVz/W,...),

Сг =А./1./гА21, Г21 Ji'dJ^dt, Lz\ ^'Wi/A²,

J^/nn, rn Ji Wdt, Ln Jt "i/Wrf”²,...),

(3.97)

C, =A^ ¹^ т;, J.'dJ/dt, L”, J.'W/dti,

J^/n„ TyJ.'dJ/dt, LyJ/W/dft....),

C„ =W^„ ^, •/>' dUdt, L„, ^"a^JJdft,

JzJJn^ r^ J,- dJJdt, Z^ Ji'¹W„/A²,...,

W^,T^J”'dJ^dt,L^J^"<PJ^dt\...).

или в случае линейной аппроксимации и некоторых перестановок составляющих

С, =J^/nn+J^2/nn+...+ ГЦ./1 'dJ\/dt + TnJ^'dJi/dt +

+ Ln /i "(PJi/dl^ + LnJ\ "(PJi/dl¹ +,...,

(3.98)

Ci =J\Ji/m\ +У2²/^^22+-+ TuJi'dJ^dt + TiiJzWdt +

+ Lu Ji" Wdt¹ + Ln Ji" ^J-i/dt¹ +,...,

С, = J.Vn,, + Л/А, +...+ TiiJi'dJ/dl + r^J.'dJ/dt +

+ Li,J," dV/A² + LyJ," cPJ/dfi +,...,

Cm ^ Jmh/nml + J^T/n^ +...+ J^mm ⁺

+ T^J^'dJtdt + -c^J^'dWl +...+ r^, J” dJ^/dl + + L„ ^ " ^Ji/A² + £w •/” " ^^A² +- + L^ d^JJdft .

204

Соотношения (3.97) и (3.98) У,' и ./."отражают динамику измене­ния / при становлении понятий о материальных свойствах или объ­ектах t'-го вида.

Для характеристики полезной производительности (информа­ционной мощности) N можно ввести выражение, аналогичное мощ­ности энергетических систем

N = dC/dt = H dJ/dl. (3.99)

Изложенное выше представляет удобную и универсальную ос­нову для формализованной оценки ряда закономерностей систем, сравнительного анализа структур и других моделей сложных про­блемных ситуаций. Примеры применения информационного подхо­да для исследования процессов управления и проектирования будут приводиться в последующих главах. В то же время исследования закономерностей систем имеют принципиальное значение для раз­вития теории систем, и поэтому рассмотрим применение изло­женного подхода для исследования одной из наиболее принципи­альных проблем этой теории - проблемы взаимодействия части и целого.