
- •Часть 2. Электростатика и постоянный ток.
- •Закон сохранения электрического заряда:
- •2.1.2. Постоянный ток
- •Контрольное задание №3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •2.2. Основные формулы и законы электромагнетизма
- •2.2.1. Электромагнетизм
- •Контрольное задание №4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
Часть 2. Электростатика и постоянный ток.
ЭЛЕКТРОМАГНЕТИЗМ
2.1. ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ ЭЛЕКТРОСТАТИКИ
И ПОСТОЯННОГО ТОКА
2.1.1. Электростатика
Закон Кулона:
 ,
,
где
 – модуль силы взаимодействия двух
точечных зарядов q1
и q2;
r
– расстояние между зарядами;
– модуль силы взаимодействия двух
точечных зарядов q1
и q2;
r
– расстояние между зарядами;
 - диэлектрическая
проницаемость среды;
- диэлектрическая
проницаемость среды;
 - электрическая постоянная:
- электрическая постоянная:
 Ф/м.
Ф/м.
Закон сохранения электрического заряда:
 ,
,
где
 – алгебраическая сумма зарядов, входящих
в изолированную систему; n
– количество
зарядов.
– алгебраическая сумма зарядов, входящих
в изолированную систему; n
– количество
зарядов.
Напряженность
электрического поля в данной точке
численно равна силе, действующей на
единичный положительный заряд
 ,
помещенный в эту точку:
,
помещенный в эту точку:
 .
.
Модуль
вектора напряженности электрического
поля, создаваемого точечным зарядом
 на расстоянии
на расстоянии
 от этого заряда:
от этого заряда:
 .
.
Поток
вектора напряженности
 электрического поля через элементарную
площадку
электрического поля через элементарную
площадку
 :
:
 ,
,
где
вектор
 ;
;
 -
единичный вектор нормали к площадке
;
-
единичный вектор нормали к площадке
;
 - угол между векторами
и
.
- угол между векторами
и
.
Согласно
принципу суперпозиции (наложения)
электрических полей, напряженность
результирующего
поля, созданного
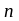 точечными зарядами, равна векторной
(геометрической) сумме напряженностей
полей, созданных каждым зарядом в
отдельности:
точечными зарядами, равна векторной
(геометрической) сумме напряженностей
полей, созданных каждым зарядом в
отдельности:
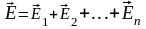 .
.
Для
двух электрических полей с напряженностями
 и
и
 модуль вектора
напряженности результирующего поля:
модуль вектора
напряженности результирующего поля:
 ,
,
где
 и
и
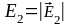 ;
;
 - угол между векторами
и
.
- угол между векторами
и
.
Теорема Остроградского-Гаусса для электростатического поля в вакууме:
 ,
,
где
 - поток
вектора напряженности
электрического поля через замкнутую
поверхность
- поток
вектора напряженности
электрического поля через замкнутую
поверхность
 ;
;
 -
проекция вектора
на единичный вектор
нормали
к площадке
-
проекция вектора
на единичный вектор
нормали
к площадке
 ;
-
алгебраическая сумма электрических
зарядов, находящихся в объеме пространства,
ограниченного замкнутой поверхностью
.
;
-
алгебраическая сумма электрических
зарядов, находящихся в объеме пространства,
ограниченного замкнутой поверхностью
.
Линейная
плотность заряда есть величина, равная
отношению модуля заряда
 ,
распределенного по нити (цилиндру), к
длине нити (цилиндра)
,
распределенного по нити (цилиндру), к
длине нити (цилиндра)
 :
:

Модуль
вектора напряженности электрического
поля, создаваемого прямой, бесконечно
длинной и равномерно заряженной нитью
(цилиндром) на расстоянии
от ее (его) оси:
 .
.
Поверхностная
плотность заряда есть величина, равная
отношению модуля заряда
,
распределенного по поверхности, к
площади
 этой
поверхности:
этой
поверхности:
 .
.
Модуль
вектора напряженности электрического
поля, создаваемого бесконечной равномерно
заряженной плоскостью:
 .
.
Модуль напряженности электрического поля, создаваемого двумя параллельными, бесконечными, разноименно заряженными плоскостями, имеющими одинаковые поверхностные плотности зарядов:
 .
.
Приведенная формула справедлива для вычисления напряженности электрического поля между пластинами плоского конденсатора в случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.
Электрический
диполь - система двух равных по модулю
разноименных точечных зарядов ( и
и
 ),
находящихся на расстоянии
),
находящихся на расстоянии
 друг
от друга.
друг
от друга.
Электрический момент диполя:
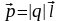 ,
,
где
 -
вектор, направленный от отрицательного
к положительному заряду, и называемый
плечом диполя.
-
вектор, направленный от отрицательного
к положительному заряду, и называемый
плечом диполя.
Модуль напряженности электрического поля диполя в точке, лежащей на прямой, совпадающей с осью диполя:
 ,
,
где
 - модуль электрического диполя,
-
расстояние от середины оси диполя до
данной точки (при
»
).
- модуль электрического диполя,
-
расстояние от середины оси диполя до
данной точки (при
»
).
Модуль напряженности электрического поля диполя в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины:
 ,
,
где - расстояние от середины плеча диполя до данной точки (при » ).
Потенциал электрического поля диполя в точке, лежащей на прямой, совпадающей с осью диполя:
 ,
,
где
-
расстояние от середины оси диполя до
данной точки (при
»
);
положительный знак соответствует
потенциалу
 точки,
лежащей на стороне заряда
;
отрицательный знак – потенциалу
точки, лежащей на стороне заряда
.
точки,
лежащей на стороне заряда
;
отрицательный знак – потенциалу
точки, лежащей на стороне заряда
.
Потенциал
электрического поля диполя в точке,
лежащей на перпендикуляре к плечу
диполя, восстановленном из его середины:
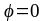 .
.
Механический
момент сил, действующих на диполь с
электрическим моментом
 ,
помещенный в однородное электрическое
поле с напряженностью
:
,
помещенный в однородное электрическое
поле с напряженностью
:
 ,
,
где
-
угол между векторами
и
;
 .
.
Потенциал
данной точки электрического поля
численно равен работе
 ,
совершаемой силами поля, по перемещению
единичного положительного заряда
из
данной точки поля в точку, в которой
потенциал считается равным нулю:
,
совершаемой силами поля, по перемещению
единичного положительного заряда
из
данной точки поля в точку, в которой
потенциал считается равным нулю:
 .
.
В
многих случаях потенциал электрического
поля в бесконечности принимается равным
нулю. Потенциал электрического поля,
создаваемого точечным зарядом
 ,
на расстоянии
от этого
заряда:
,
на расстоянии
от этого
заряда:
 .
.
Потенциал
электрического поля, создаваемого
металлической сферой радиусом
 с общим
зарядом
на расстоянии
от
центра этой сферы:
с общим
зарядом
на расстоянии
от
центра этой сферы:
а)
внутри сферы (
<
) и на поверхности сферы (
=
)
-
 ;
;
б) вне сферы ( > ) - .
Потенциал
электрического поля, созданного системой
точечных зарядов, в данной точке, в
соответствии с принципом суперпозиции
электрических полей, равен алгебраической
сумме потенциалов ,
создаваемых отдельными точечными
зарядами
,
создаваемых отдельными точечными
зарядами

 .
.
Совокупность точек, имеющих одинаковые потенциалы, называется эквипотенциальной поверхностью.
Потенциальная энергия электрического заряда , находящегося в некоторой точке электрического поля:
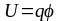 ,
,
где - потенциал этой точки электрического поля.
Работа,
совершаемая силами электрического поля
при перемещении точечного заряда
из
одной точки поля, имеющей потенциал
 ,
в другую, имеющую потенциал
,
в другую, имеющую потенциал
 :
:
 .
.
Энергия
 взаимодействия системы точечных
электрических зарядов
взаимодействия системы точечных
электрических зарядов
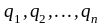 равна работе, которую могут совершить
силы электрического поля при удалении
этих зарядов относительно друг друга
в бесконечность:
равна работе, которую могут совершить
силы электрического поля при удалении
этих зарядов относительно друг друга
в бесконечность:
 ,
,
где
 -
потенциал точки поля, в которой находится
заряд
-
потенциал точки поля, в которой находится
заряд
 ,
создаваемый всеми зарядами, кроме i-ым.
,
создаваемый всеми зарядами, кроме i-ым.
Если известен потенциал каждой точки электрического поля, то напряженность этого поля равна отрицательному градиенту потенциала:
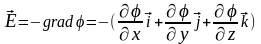 ,
,
где
 ;
;
 - частные производные функции
по координатам
- частные производные функции
по координатам
 ;
;
 - единичные векторы координатных осей
.
- единичные векторы координатных осей
.
В
случае однородного электрического поля
( )
модуль напряженности этого поля:
)
модуль напряженности этого поля:
 ,
,
где
и
- потенциалы двух точек, находящихся
на эквипотенциальных поверхностях,
расстояние между которыми равно
 .
.
Поляризованностью
 называется
дипольный электрический момент единицы
объема диэлектрика:
называется
дипольный электрический момент единицы
объема диэлектрика:
 ,
,
где
 -
векторная сумма электрических дипольных
моментов молекул;
-
векторная сумма электрических дипольных
моментов молекул;
 -
объем диэлектрика.
-
объем диэлектрика.
Если диэлектрик изотропный и внутри его напряженность электрического поля не слишком велика, то:
=
æ ,
,
где æ – диэлектрическая восприимчивость вещества.
Поверхностная
плотность связанных зарядов, индуцируемых
внешним электрическим полем в диэлектрике:
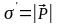 .
.
Диэлектрическая
проницаемость среды:
 æ.
æ.
Вектор
электрического смещения
 характеризует
электростатическое поле, создаваемое
свободными зарядами при наличии
диэлектрика, в котором индуцируются
связанные заряды:
характеризует
электростатическое поле, создаваемое
свободными зарядами при наличии
диэлектрика, в котором индуцируются
связанные заряды:
 ,
,
где - напряженность электрического поля внутри диэлектрика.
Вектор электрического смещения связан с поляризованностью :

Теорема Гаусса для электростатического поля в диэлектрике:

где
 - поток
вектора электрического смещения
через замкнутую поверхность
;
- поток
вектора электрического смещения
через замкнутую поверхность
;
 -
проекция вектора
на единичный
вектор нормали
к
площадке
;
-
алгебраическая сумма свободных
электрических зарядов, находящихся в
объеме пространства, ограниченного
замкнутой поверхностью
.
-
проекция вектора
на единичный
вектор нормали
к
площадке
;
-
алгебраическая сумма свободных
электрических зарядов, находящихся в
объеме пространства, ограниченного
замкнутой поверхностью
.
Электроемкость
уединенного проводника, имеющего
электрический заряд
и потенциал
:
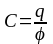 .
.
Электроемкость
уединенной проводящей сферы радиусом
,
находящейся в бесконечной среде с
диэлектрической проницаемостью
:
 .
.
Электроемкость
конденсатора:
 ,
,
где
-
модуль электрического заряда, находящегося
на каждой обкладки конденсатора;
 -
разность потенциалов между обкладками
конденсатора.
-
разность потенциалов между обкладками
конденсатора.
Электроемкость
плоского конденсатора:
 ,
,
где - площадь одной обкладки конденсатора; - расстояние между обкладками конденсатора.
Электроемкость
плоского конденсатора, заполненного
слоями
диэлектриков с диэлектрическими
проницаемостями
 и толщинами
и толщинами
 :
:
 .
.
Электроемкость
сферического конденсатора (две
концентрические сферы с радиусами
 и
и
 ),
пространство между которыми заполнено
диэлектриком с диэлектрической
проницаемостью
:
),
пространство между которыми заполнено
диэлектриком с диэлектрической
проницаемостью
:

Электроемкость
 последовательно
соединенных
конденсаторов:
последовательно
соединенных
конденсаторов:
 .
.
Электроемкость параллельно соединенных конденсаторов:
 .
.
Энергия
заряженного конденсатора:
 ,
,
где
-
электроемкость;
-
электрический заряд конденсатора;
 - разность потенциалов между обкладками
конденсатора.
- разность потенциалов между обкладками
конденсатора.
Объемная плотность энергии электростатического поля (энергия единицы
объема):
 ,
,
где
 -
модуль вектора напряженности электрического
поля;
-
модуль вектора напряженности электрического
поля;
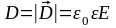 -модуль
вектора электрического смещения.
-модуль
вектора электрического смещения.
