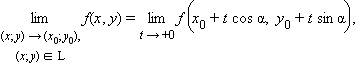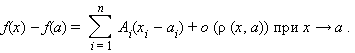Задание для самостоятельной работы:
Вычислите несобственные интегралы:
Рекомендуемая литература: 1.1, 1.2,2.2.
Самостоятельная работа №8
Тема: «Частные производные функций нескольких действительных переменных»
Цель: Формирование навыков вычисления частных производных и дифференциалов функций нескольких переменных
Время выполнения: 5 часов
Теоретические сведения
В природе иногда
встречаются процессы, в которых
исследуемая величина является функцией
двух, трех и т. д. других величин. Так,
в термодинамике температура идеального
газа T зависит от давления p и
объема V. Если каждому набору
аргументов
…,
ставится
в соответствие число
то
говорят, что задана функция n переменных
y = f (x1, x2, …, xn). |
Число A называется пределом функции f (x1, x2, …, xn) по подмножеству M области определения функции при (x1; x2; …; xn) → (a1; a2; …; an), если для любого ε > 0 существует такое δ > 0, что на пересечении δ-окрестности точки A (кроме, быть может, самой точки A) с подмножеством M для всех x = (x1; x2; …; xn) выполняется неравенство
|f (x) – A| < ε. |
В этом
случае пишут
Пусть функция двух переменных f (x, y) определена в некоторой окрестности точки (x0; y0). Пределом функции f (x, y) в точке (x0; y0) по направлению l = (cos α, sin α) называется число
|
где L – луч, выходящий из точки (x0; y0) в направлении l.
Пусть
функция f (x1, x2, …, xn)
определена в окрестности точки
a = (a1; a2; …; an).
Рассмотрим функцию одной переменной
f (x1, a2, …, an).
Она может иметь производную по своей
переменной x1.
Такая производная по определению
называется частной производной 
в точке
|
Аналогично определяются частные производные функции f по другим переменным.
Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, правила вычисления частной производной точно такие же, как и обычной производной.
Функция f (x1, x2, …, xn) называется дифференцируемой в точке a = (a1; a2; …; an), если она определена в некоторой окрестности этой точки и существуют такие числа A1, A2, …, An, что
|
Функция f (x1, x2, …, xn) дифференцируема в точке a тогда и только тогда, когда в некоторой окрестности a функция f (x) может быть представлена в следующем виде:
|
где
функции
непрерывны
в точке a.
Если
функция
дифференцируема
в точке a,
то в окрестности a
существуют все частные производные
и
|
Обратное, вообще говоря, неверно.
Задание для самостоятельной работы
Подготовить сообщение на тему «Приложения частных производных»
Рекомендуемая литература: 1.1,1.2, 1.3, 2.1, 2.2.
Самостоятельная работа №9
Тема: «Вычисление двойных интегралов»
Цель: Формирование навыков изменять порядок интегрирования, вычислять двойные интегралы в декартовых координатах.
Время выполнения: 5 часов