Примеры

Задание 1: Найти сумму и разность матриц и .

Решение: Здесь даны матрицы одного размера , следовательно, существуют их сумма и разность. Согласно определению алгебраической суммы матриц имеем

,

.

Задание 2: Вычислить определители: 1) ; 2) .

Решение: 1) По формуле (1) находим .

2) Разлагая данный определитель, например, по элементам первой строки, находим

.

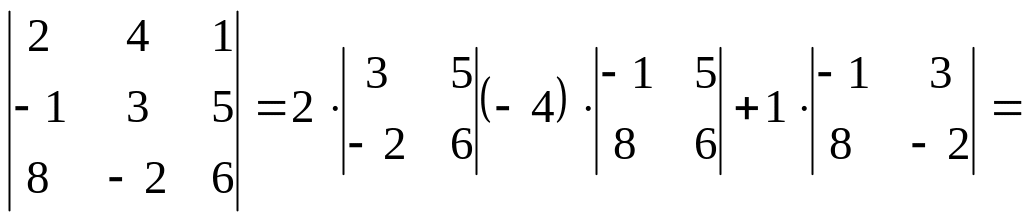
Тот же результат получится, если воспользоваться формулой (2):

.

Задания для самостоятельной работы

1. Найдите сумму матриц и .

2. Транспонируйте матрицу . Укажите размеры данной и транспонированной матриц.

3. Даны матрицы: , . Произведите указанные действия, а в случае, когда это невозможно, указать причину: 1) ;

2) .

4. Даны матрицы и 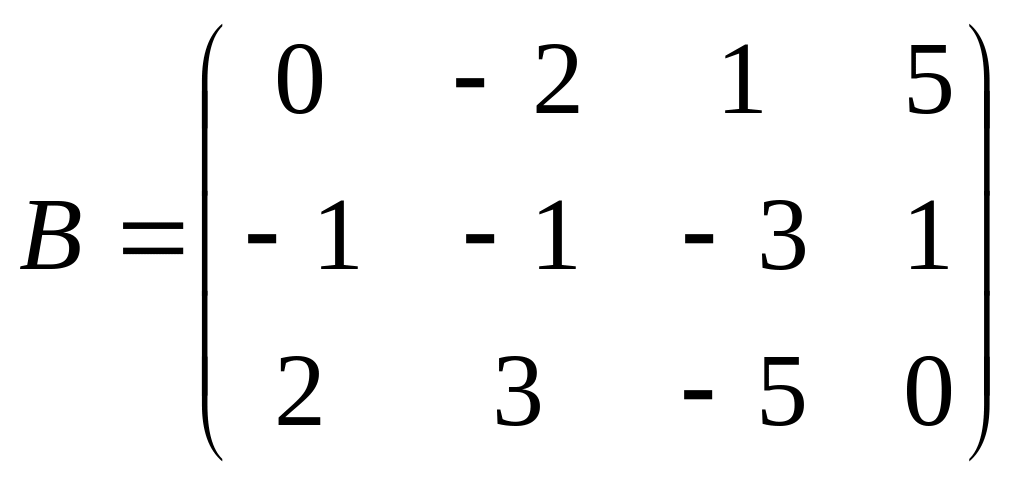. Найдите матрицу .

5. Вычислите определители второго порядка: а) ;

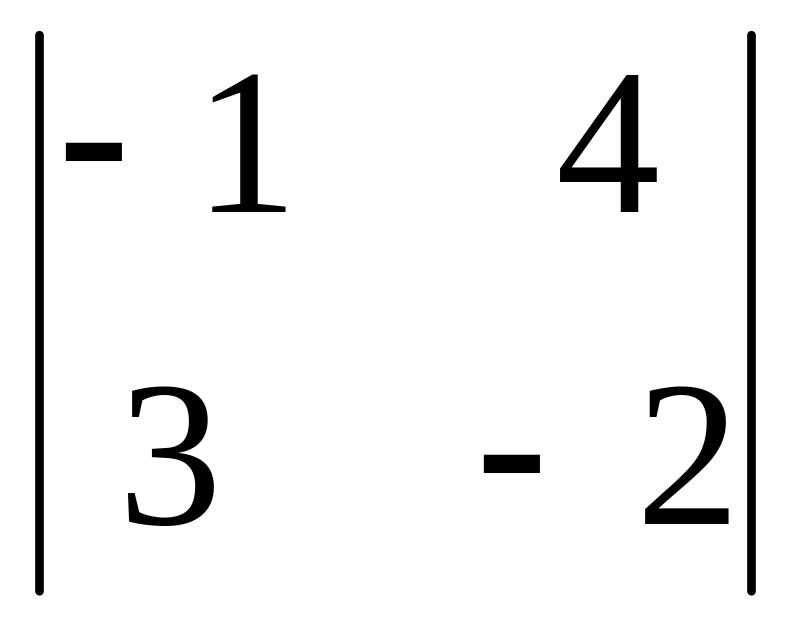б) .

6. Вычислите определители третьего порядка: а) ;

б) .

7. Вычислите определитель четвертого порядка .

Вопросы для самоконтроля:

1. Что называется матрицей? Как установить размеры матрицы?

2. Назовите линейные операции над матрицами. Как они производятся?

3. Какие матрицы можно перемножать? Как это делается?

4. Что называется определителем? Как вычисляются определители второго и третьего порядков?

5. Что называется минором и алгебраическим дополнением для произвольного элемента определителя?

Практическое занятие №2 Тема: Нахождение обратной матрицы

Цель: Формирование навыков нахождения обратной матрицы.

На выполнение практической работы отводится 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Матрица, состоящая из строк и столбцов, называется квадратной матрицей порядка :

.

Элементы образуют главную диагональ матрицы.

У единичной матрицы порядка элементы главной диагонали равны единицы, а остальные элементы равны нулю: то есть

.

Для - матриц справедливы равенства .

Каждой - матрице соответствует определитель -го порядка, который состоит из тех же элементов, расположенных в том же порядке, что и в матрице:

.

Произведение двух квадратных матриц всегда определено; при этом определитель матрицы – произведения равен произведению определителей матриц – сомножителей: .

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля , и вырожденной в противном случае .

Всякая невырожденная матрица порядка имеет обратную матрицу того же порядка , удовлетворяющую соотношениям

.

Обратная матрица имеет вид

, (1)

где - алгебраическое дополнение элемента в определителе матрицы , то есть элементы обратной матрицы находятся по формулам .

Свойства обратной матрицы

(здесь - матрицы, - число)

1. ;

2. ;

3. ;

4. ;

5. .

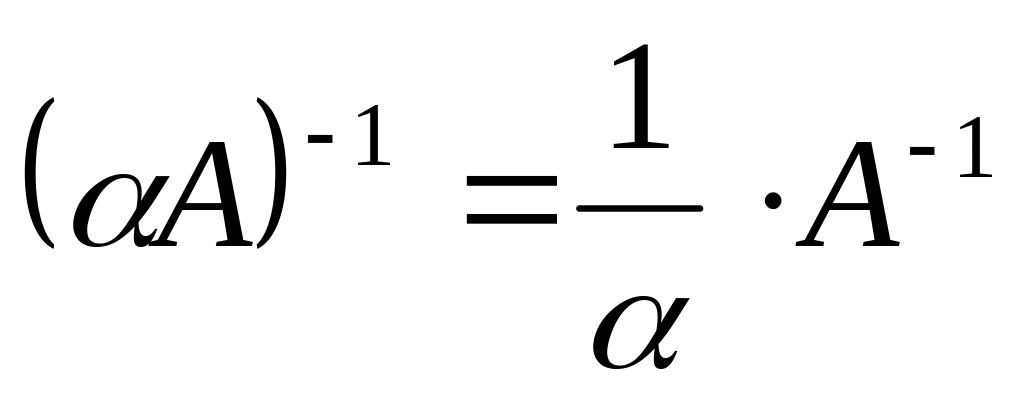Пример

Задание: Для матрицы найти обратную матрицу и проверить, что .

Решение: Так как , то матица имеет обратную матрицу, элементы которой равны .

Вычислим алгебраические дополнения элементов для :

; ;

; ;

; ;

; ;

.

Теперь, используя формулу (1), находим обратную матрицу

.

Далее вычислим произведение

=

= .

Аналогично находим

. Итак, обратная матрица вычислена правильно.