
- •Линейные электрические цепи постоянного тока
- •Содержание
- •1Основные законы и методы преобразования линейных электрических цепей постоянного тока
- •1.1Основные понятия и определения
- •1.2Закон Ома для участка линейной электрической цепи постоянного тока
- •1.3Идеальные и реальные источники электрической энергии. Закон Ома для полной цепи
- •1.4Последовательное и параллельное соединение проводников (потребителей)
- •1.5Законы Кирхгофа
- •1.6Эквивалентные преобразования в линейных электрических цепях
- •1.7Перенос источников энергии через узел
1.4Последовательное и параллельное соединение проводников (потребителей)
На практике проводники в электрических
цепях могут соединяться последовательно
и параллельно. При последовательном
соединении
![]() проводников (потребителей) конец первого
проводника (потребителя) соединяется
с началом второго и т.д. (см. рисунок 1 .9)
проводников (потребителей) конец первого
проводника (потребителя) соединяется
с началом второго и т.д. (см. рисунок 1 .9)
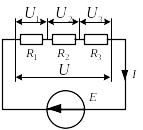
Рисунок 1.9 – Последовательное соединение трех потребителей
При этом сила тока одинакова во всех проводниках:
![]() , (1.12)
, (1.12)
а напряжение на концах всей цепи равно сумме напряжений на всех последовательно включенных проводниках:
![]() (1.13)
(1.13)
Например, для трех последовательно
включенных проводников 1, 2, 3 (см. рисунок
1 .9) с электрическими сопротивлениями
![]() ,
,
![]() и
и
![]() получим
получим
![]() .
.
По закону Ома для участка цепи
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
где
– полное сопротивление участка цепи
из последовательно включенных проводников.
Поэтому
,
где
– полное сопротивление участка цепи
из последовательно включенных проводников.
Поэтому
![]() .
Таким образом,
.
Таким образом,
![]() .
.
При последовательном соединении проводников их общее электрическое сопротивление равно сумме электрических сопротивлений всех проводников, т.е.
![]() (1.14)
(1.14)
При параллельном соединении проводников (потребителей) их начала и концы имеют общие точки подключения к источнику энергии (см. рисунок 1 .10).
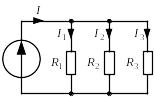
Рисунок 1.10 – Параллельное соединение трех потребителей
При этом напряжение на всех проводниках одинаково:
![]() , (1.15)
, (1.15)
а сила тока
![]() в неразветвленной цепи равна сумме сил
токов во всех параллельно включенных
проводниках:
в неразветвленной цепи равна сумме сил
токов во всех параллельно включенных
проводниках:
![]() (1.16)
(1.16)
Для трех параллельно включенных проводников 1, 2, 3 (см. рисунок 1 .10) сопротивлениями , и на основании закона Ома для участка цепи запишем
 ,
,
 ,
,
 .
.
Обозначив общее сопротивление участка электрической цепи из трех параллельно включенных проводников через , для силы тока в неразветвленной цепи получим
.
Так как
![]() ,
то
,
то
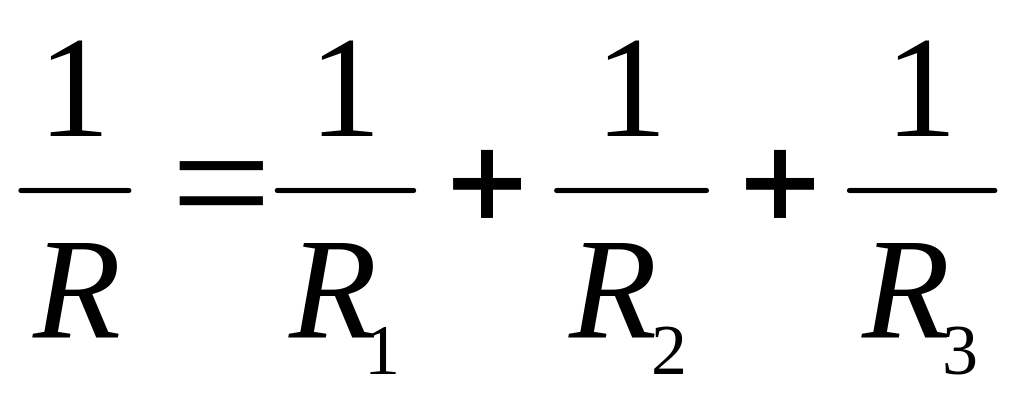 .
.
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям всех параллельно включенных проводников:
 (1.17)
(1.17)
Иногда, чтобы показать, что сопротивление
состоит из
параллельно соединенных резисторов
![]() прибегают к записи вида
прибегают к записи вида
![]()
Параллельный способ включения широко применяется для подключения ламп электрического освещения и бытовых электроприборов к электрической сети.
Определенный интерес представляет собой случай нахождения тока ветви в схеме, изображенной на рисунке 1 .11.

Рисунок 1.11 – Параллельное соединение двух потребителей
Пусть известны ток
в неразветвленной части схемы и
сопротивления
и
.
Требуется найти токи в ветвях. Так как
и
соединены параллельно, то
![]() ,
где
,
где
![]() – напряжение между точками
и
,
– напряжение между точками
и
,
![]() ,
,
![]() – напряжения соответственно на резисторах
и
.
Кроме того,
– напряжения соответственно на резисторах
и
.
Кроме того,
 .
С другой стороны,
.
С другой стороны,
![]() и
и
![]() .
Таким образом,
.
Таким образом,
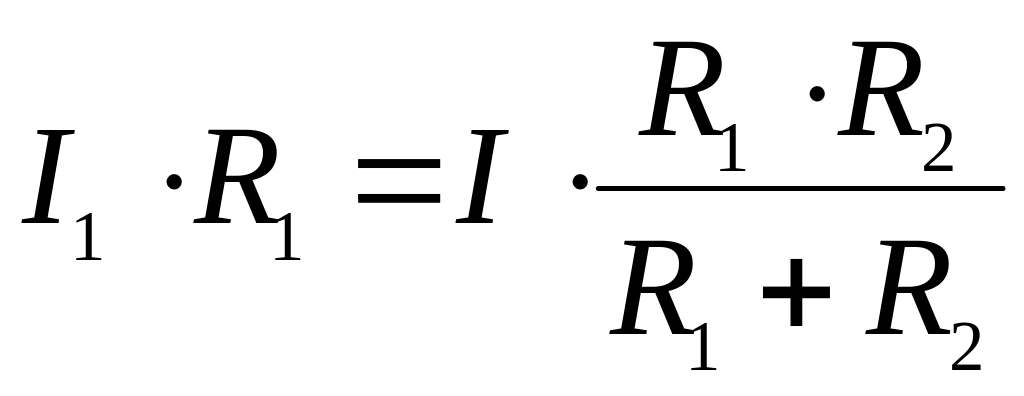 и
и
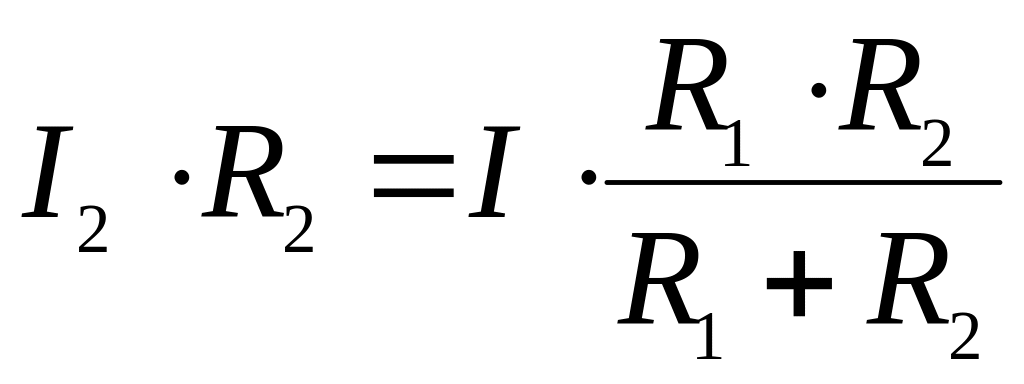 ,
откуда, разделив обе части равенства
на
в первом выражении и на
– во втором, получим:
,
откуда, разделив обе части равенства
на
в первом выражении и на
– во втором, получим:

Для того чтобы найти «собственный» ток (то есть ток через рассматриваемую ветвь) необходимо ток в неразветвленной части цепи умножить на «чужое» сопротивление (то есть сопротивление параллельной ветви) и разделить на сумму «своего» и «чужого» сопротивлений.
