
Практические работы / пр 4 / пр 4
.docxПрактическая работа №4
СМО с очередью
Ход работы
Задание: выполним моделирование, используя следующие исходные данные: tz=8 мин., to=7 мин.; 0 t =9 ч.; LOMax =1 (время между заявками и обслуживания является случайными величинами с показательным законом распределения)
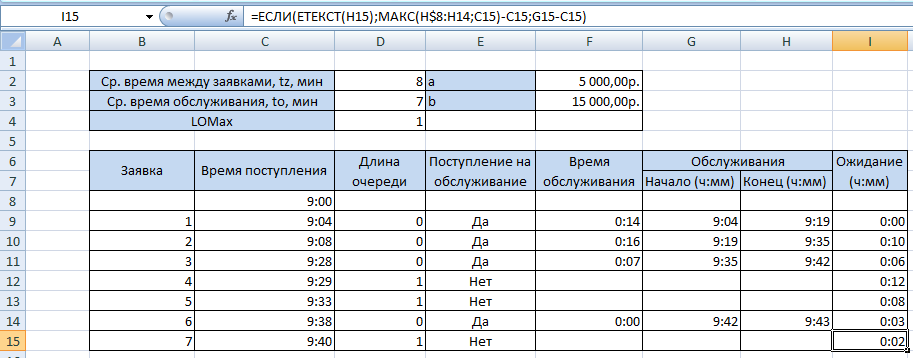
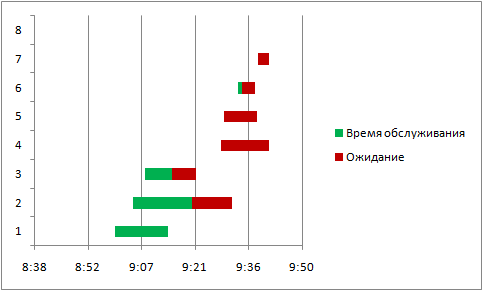
Формулы:
С9=C8+(-$D$2*LN(СЛЧИС())/1440)
D9=СЧЁТЕСЛИ($G$8:$G8;">"&C9)
E9=ЕСЛИ(D9>$E$4;"Нет";"Да")
F9=ЕСЛИ(E9="Нет";"";-$D$2*LN(СЛЧИС())/1440)
G9=ЕСЛИ(E9="Да";МАКС(C9;H$8:H8);"")
H9=ЕСЛИ(ЕТЕКСТ(G9);"";G9+F9)
I=ЕСЛИ(ЕТЕКСТ(H9);МАКС(H$8:H8;C9)-C9;G9-C9)
Самостоятельная работа
Задание 1.Парикмахерская занимается обслуживанием клиентов. Время между приходом двух клиентов является случайной величиной с показательным законом распределения (среднее значение - tz), а время обслуживания распределено по нормальному закону. В том случае, если в момент прихода нового клиента мастер занят, то клиент встает в очередь.
При этом имеются места ожидания, число которых равно LOMax.Если же все места заняты, то клиент уходит и не ждет обслуживания. Выручка от одного клиента, а также его время обслуживания зависит от типа прически.
В таблице 1 приведены характеристики этих данных.
Таблица 1 – Характеристики причесок
|
Тип прически |
1 |
2 |
3 |
4 |
|
Стоимость,руб. |
100 |
120 |
140 |
150 |
|
Среднее время обслуживания, мин. |
15 |
20 |
20 |
25 |
|
СКО времени обслуживания, мин. |
3 |
3 |
5 |
6 |
Также имеются следующие статистические данные о том, сколько людей выбрало тот или иной тип прически (всего 100 человек)
|
Тип прически |
1 |
2 |
3 |
4 |
|
Число людей |
20 |
30 |
35 |
15 |
Выполните моделирование поступления 9 заявок, используя следующие исходные данные: tz=20 мин.; LOMax =2; tn=9 ч.
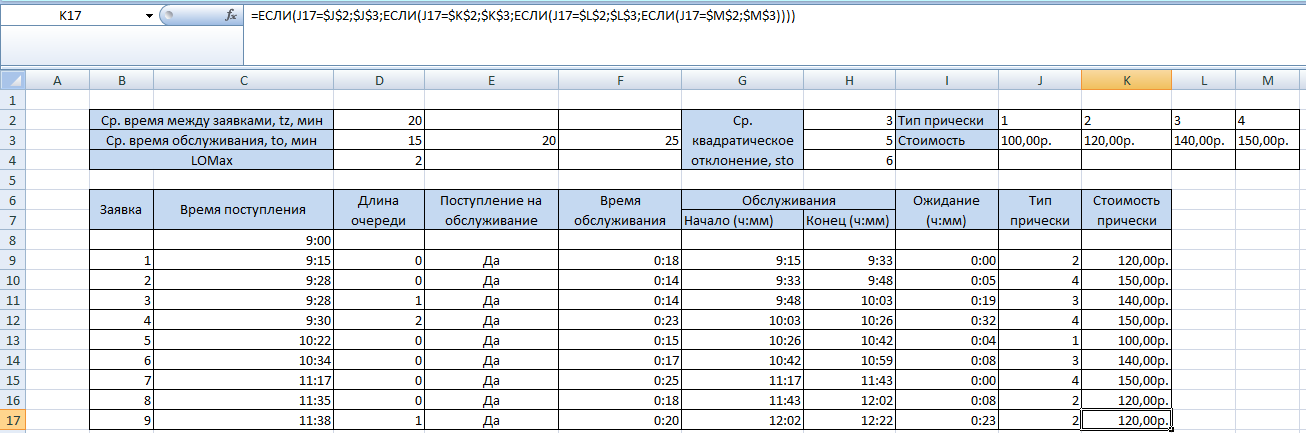
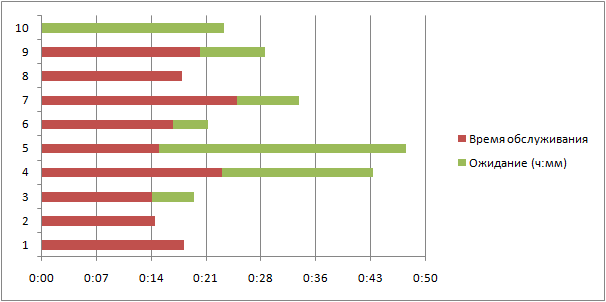
Формулы:
E9=ЕСЛИ(МАКС($H$8:H8)>=C9;ЕСЛИ(D9>$D$4;"Нет";"Да");"Да")
F9=ЕСЛИ(E9="Нет";"";ЕСЛИ(J9=$J$2;НОРМОБР(СЛЧИС();$D$3;$H$2)/1440;ЕСЛИ(J9=$K$2;НОРМОБР(СЛЧИС();$E$3;$H$2)/1440;ЕСЛИ(J9=$L$2;НОРМОБР(СЛЧИС();$E$3;$H$3)/1440;ЕСЛИ(J9=$M$2;НОРМОБР(СЛЧИС();$F$3;$H$4)/1440)))))
J9=СЛУЧМЕЖДУ($J$2;$M$2)
K9=ЕСЛИ(J9=$J$2;$J$3;ЕСЛИ(J9=$K$2;$K$3;ЕСЛИ(J9=$L$2;$L$3;ЕСЛИ(J9=$M$2;$M$3))))
Формулы:
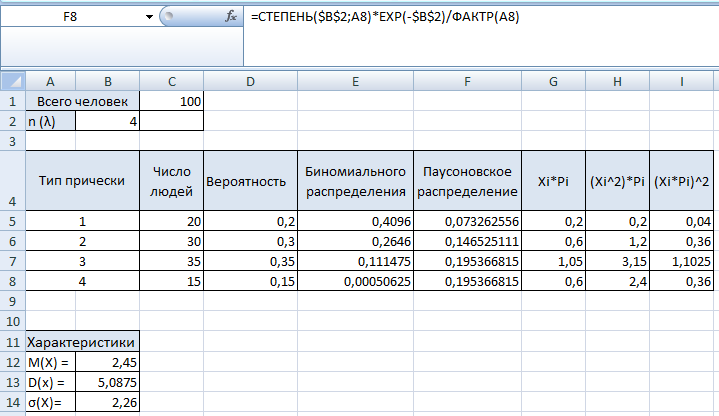
D5=C5/$C$1
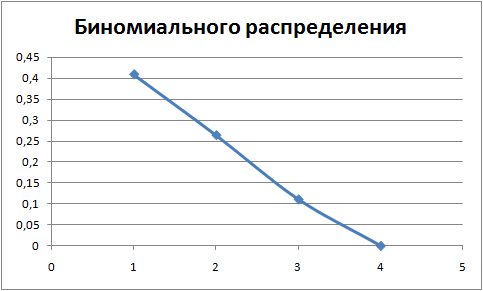
E5=БИНОМРАСП(A5;$B$2;D5;0)
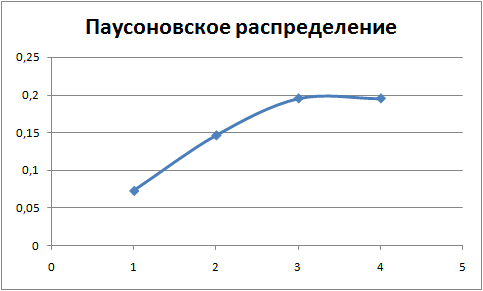
F5=СТЕПЕНЬ($B$2;A5)*EXP(-$B$2)/ФАКТР(A5)
G5=ПРОИЗВЕД(A5;D5)
H5=(A5^2)*D5
I5=СТЕПЕНЬ(A5*D5;2)
B12=СУММ(G5:G8)
B13=СУММ(H5:H8)-СУММ(I5:I8)
B14=КОРЕНЬ(B13)
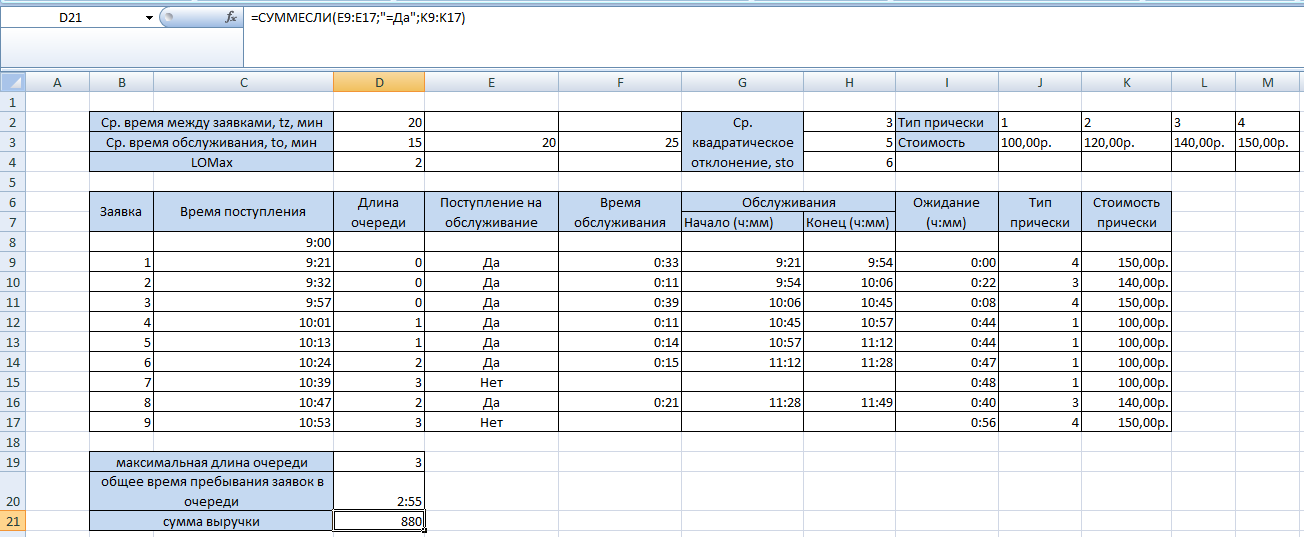
Задание 2. Рассчитайте следующие значения: максимальная длина очереди; общее время пребывания заявок в очереди; сумма выручки.
Формулы:
D19=МАКС(D9:D17)
D20=СУММЕСЛИМН(I9:I17;E9:E17;"=Да";D9:D17;">0")
D21=СУММЕСЛИ(E9:E17;"=Да";K9:K17)
Задание 3. Проведите 10 экспериментов и рассчитайте величины:
• среднее число отказов в обслуживании;
• среднюю выручку;
• среднее время завершения моделирования (время окончания обслуживания последней заявки).

Формулы:
D20=СЧЁТЕСЛИМН(E9:E18;"=Нет")/10
D21=СУММЕСЛИ(E9:E17;"=Да";K9:K17)/10
D22=МАКС(H9:H18)
