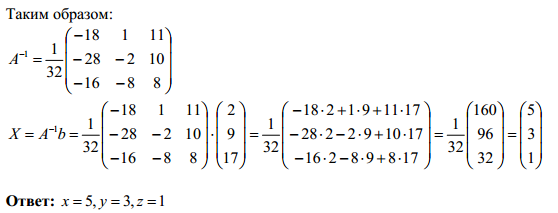- •Практикум по линейной алгебре
- •Тема 3. Действия с матрицами. Метод обратной матрицы для решения слау. Действия с матрицами
- •Действия с матрицами
- •1. Вынесение минуса из матрицы (внесение минуса в матрицу).
- •2. Умножение матрицы на число.
- •3. Транспонирование матрицы
- •5. Умножение матриц.
- •6. Нахождение обратной матрицы.
- •Алгебраические дополнения и миноры. Теоретическая справка.
- •2) Находим матрицу миноров
- •3) Находим матрицу алгебраических дополнений
- •4) Находим транспонированную матрицу алгебраических дополнений .
- •5) Ответ.
- •1) Находим определитель матрицы.
- •2) Находим матрицу миноров
- •3) Находим матрицу алгебраических дополнений
- •4) Находим транспонированную матрицу алгебраических дополнений .
- •5) Ответ:
- •Метод обратной матрицы
1) Находим определитель матрицы.
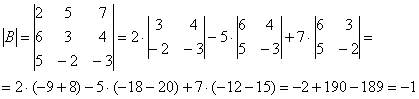 Здесь
определитель раскрыт по
первой строке.
Здесь
определитель раскрыт по
первой строке.
Проверка. ![]() ,
а значит, обратная
матрица существует.
,
а значит, обратная
матрица существует.
2) Находим матрицу миноров
Матрица
миноров имеет размерность «три на
три»  .
.
Здесь подробно рассмотрено нахождение одного минора:
Рассмотрим
следующий элемент матрицы:
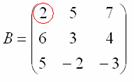 МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:
МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:
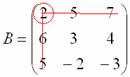
Оставшиеся
четыре числа записываем в определитель
«два на два»
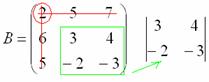 Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
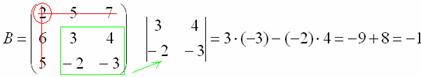 Записываем
полученное значение в матрицу
миноров:
Записываем
полученное значение в матрицу
миноров:
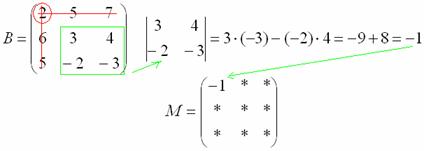 Остальные
миноры вычислить самостоятельно.
Остальные
миноры вычислить самостоятельно.
Окончательный
результат:
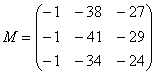 –
матрица миноров соответствующих
элементов матрицы
–
матрица миноров соответствующих
элементов матрицы ![]() .
.
То, что все миноры получились отрицательными – чистая случайность.
3) Находим матрицу алгебраических дополнений
В
матрице миноров необходимо СМЕНИТЬ
ЗНАКИ строго
у следующих элементов:
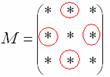 В
данном случае:
В
данном случае:
 –
матрица алгебраических дополнений
соответствующих элементов матрицы
.
–
матрица алгебраических дополнений
соответствующих элементов матрицы
.
4) Находим транспонированную матрицу алгебраических дополнений .
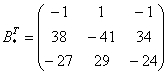 –
транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы
.
–
транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы
.
5) Ответ:
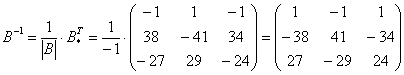
Проверка:
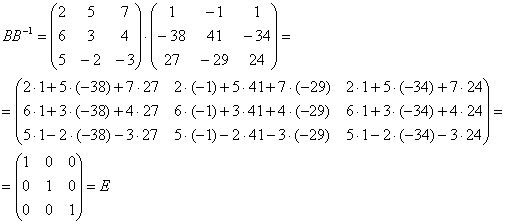
Также существует несколько другой подход к нахождению обратной матрицы. Справа к матрице приписывается единичная матрица и выполняются преобразования по методу Гаусса. В итоге слева будет получена единичная матрица, а справа как раз необходимая нам обратная.
Рекомендуется вычислять обратную матрицу с помощью первого способа, так как гораздо меньше вероятность запутаться в вычислениях и знаках.
Метод обратной матрицы
Пример.
Решить систему матричным методом
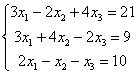
Решение:
Запишем систему в матричной форме:
![]() ,
где
,
где 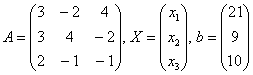
Комментарий. Если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Решение системы найдем по формуле
![]() .
.
Согласно
формуле нам нужно найти обратную
матрицу ![]() и
выполнить матричное умножение
и
выполнить матричное умножение ![]() .
.
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.
Внимание!
Если ![]() ,
то обратной матрицы не существует, и
решить систему матричным методом
невозможно. В этом случае система
решается методом
исключения неизвестных (методом Гаусса).
,
то обратной матрицы не существует, и
решить систему матричным методом
невозможно. В этом случае система
решается методом
исключения неизвестных (методом Гаусса).
Теперь
нужно вычислить 9 миноров и записать их
в матрицу миноров 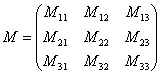
В ходе решения расчет миноров лучше расписать подробно:.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Порядок расчета миноров совершенно не важен, здесь они вычислены слева направо по строкам. Можно было рассчитать миноры по столбцам.
Таким образом:
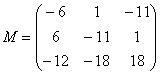 –
матрица
миноров соответствующих элементов
матрицы
.
–
матрица
миноров соответствующих элементов
матрицы
.
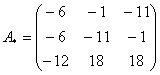 –
матрица
алгебраических дополнений.
–
матрица
алгебраических дополнений.
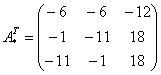 –
транспонированная
матрица алгебраических дополнений.
–
транспонированная
матрица алгебраических дополнений.
Теперь
записываем обратную матрицу:
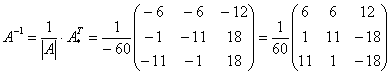
Ни
в коем случае не вносим ![]() в
матрицу, это серьезно затруднит дальнейшие
вычисления. Деление
нужно было бы выполнить, если бы все
числа матрицы делились на 60 без остатка.
А вот внести минус в матрицу в данном
случае очень даже нужно, это, наоборот
– упростит дальнейшие вычисления.
в
матрицу, это серьезно затруднит дальнейшие
вычисления. Деление
нужно было бы выполнить, если бы все
числа матрицы делились на 60 без остатка.
А вот внести минус в матрицу в данном
случае очень даже нужно, это, наоборот
– упростит дальнейшие вычисления.
Осталось провести матричное умножение.
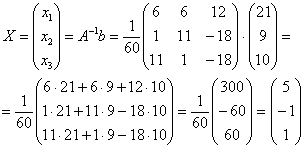
Обратите
внимание, что деление на 60 выполняется в
последнюю очередь.
Ответ: ![]()
Пример.
Решить систему с
помощью обратной матрицы.
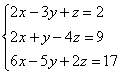
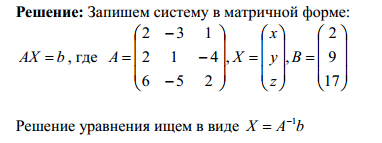
Действуем по алгоритму: