
- •Практикум по линейной алгебре
- •Тема 3. Действия с матрицами. Метод обратной матрицы для решения слау. Действия с матрицами
- •Действия с матрицами
- •1. Вынесение минуса из матрицы (внесение минуса в матрицу).
- •2. Умножение матрицы на число.
- •3. Транспонирование матрицы
- •5. Умножение матриц.
- •6. Нахождение обратной матрицы.
- •Алгебраические дополнения и миноры. Теоретическая справка.
- •2) Находим матрицу миноров
- •3) Находим матрицу алгебраических дополнений
- •4) Находим транспонированную матрицу алгебраических дополнений .
- •5) Ответ.
- •1) Находим определитель матрицы.
- •2) Находим матрицу миноров
- •3) Находим матрицу алгебраических дополнений
- •4) Находим транспонированную матрицу алгебраических дополнений .
- •5) Ответ:
- •Метод обратной матрицы
6. Нахождение обратной матрицы.
Важно! 1. Понятие обратной матрицы существует только для квадратных матриц.
2. Если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
Обозначение. Обратная
матрица обозначается надстрочным
индексом ![]() .
.
Формула
для нахождения обратной матрицы ![]() :
:
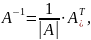 где
где ![]() –
определитель матрицы
–
определитель матрицы ![]() ,
, 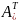 –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
Алгебраические дополнения и миноры. Теоретическая справка.
Пусть
имеем определитель третьего порядка:  .
.
Минором, соответствующим данному элементу aij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу aij будем обозначать Mij.
Например,
минором M12,
соответствующим элементу a12,
будет определитель 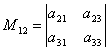 ,
который получается вычёркиванием из
данного определителя 1-ой строки и 2-го
столбца.
,
который получается вычёркиванием из
данного определителя 1-ой строки и 2-го
столбца.
Алгебраическим дополнением элемента aij определителя называется его минор Mij, умноженный на (–1)i+j.
Алгебраическое дополнение элемента aij обозначается Aij.
Связь между алгебраическим дополнением элемента и его минором выражается равенством:
Aij = (–1)i+jMij.
Например, ![]()
Пример. Дан
определитель 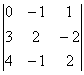 .
Найти A13,
A21,
A32.
.
Найти A13,
A21,
A32.
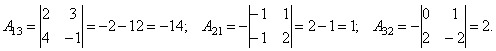
Возвращаемся к нахождению обратной матрицы.
Пример:
Найти
обратную матрицу для матрицы ![]()
Решаем. Последовательность действий по пунктам:
1) Сначала находим определитель матрицы.
![]()
Важно! Проверить существование обратной матрицы, сравнив полученное значение с 0.
В
рассматриваемом примере
![]() ,
а значит, можно решать дальше.
,
а значит, можно решать дальше.
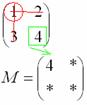
2) Находим матрицу миноров
Матрица
миноров имеет такие же размеры, как и
матрица
,
то есть в данном случае ![]() .
.
Сначала
рассмотрим левый верхний элемент матрицы
А
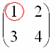 Как
найти его минор?
Мысленно
вычеркиваем строку и столбец, в котором
находится данный элемент:
Как
найти его минор?
Мысленно
вычеркиваем строку и столбец, в котором
находится данный элемент:
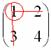 Оставшееся
число и является минором
данного элемента,
которое записываем в нашу матрицу
миноров:
Оставшееся
число и является минором
данного элемента,
которое записываем в нашу матрицу
миноров:
 Рассматриваем
следующий элемент матрицы
:
Рассматриваем
следующий элемент матрицы
:
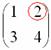 Мысленно
вычеркиваем строку и столбец, в котором
стоит данный элемент:
Мысленно
вычеркиваем строку и столбец, в котором
стоит данный элемент:
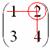 То,
что осталось, и есть минор данного
элемента, который записываем в нашу
матрицу:
То,
что осталось, и есть минор данного
элемента, который записываем в нашу
матрицу:
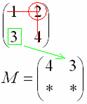 Аналогично
рассматриваем элементы второй строки
и находим их миноры:
Аналогично
рассматриваем элементы второй строки
и находим их миноры:
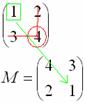
![]() –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
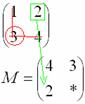
3) Находим матрицу алгебраических дополнений
В
матрице миноров нужно ПОМЕНЯТЬ
ЗНАКИ у
двух чисел, которые обведены в кружок:
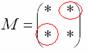
![]() –
матрица алгебраических дополнений
соответствующих элементов матрицы
.
–
матрица алгебраических дополнений
соответствующих элементов матрицы
.
4) Находим транспонированную матрицу алгебраических дополнений .
![]() –
транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы
.
–
транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы
.
5) Ответ.
Вспоминаем
формулу ![]() Таким
образом, обратная матрица:
Таким
образом, обратная матрица:
![]()
Ответ лучше оставить в таком виде.
Как
проверить решение?
Необходимо
выполнить матричное умножение ![]() либо
либо ![]()
Проверка:
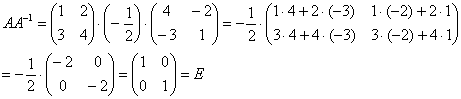
Получена единичная матрица.
Таким образом, обратная матрица найдена правильно.
Переходим к более распространенному на практике случаю – матрице «три на три».
Пример:
Найти
обратную матрицу для матрицы 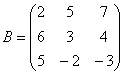
Алгоритм точно такой же, как и для случая «два на два».
