11. Привести и пояснить кривую интенсивности отказов для трёх периодов работы технического устройства.

При рассмотрении работоспособности какого-либо технического устройства или изделия различают три периода его «жизни»: период приработки, когда при испытании устройства или изделия происходит отбраковка конструктивных, технологических и производственных дефектов, период нормальной эксплуатации, характеризующийся внезапными отказами приблизительно постоянной интенсивности, и период старения, когда появляются отказы возрастающей интенсивности, вызываемые износом устройства или изделия

12. Как посчитать надёжность системы из двух элементов, соединённых последовательно и параллельно?

1. Если P1(t)—надежность одного элемента системы, а Р2(t) – надежность другого, то вероятность того, что оба элемента будут работать безотказно в течение заданного промежутка времени t, будет

2. Вероятность того, что один или оба элемента системы откажут,

3. Вероятность того, что будут работать один или два элемента системы,

4. Вероятность того, что оба элемента откажут,

Величина Р_ПС(t) является надежностью последовательно соединенных элементов системы, а величина Q_ПС(t) —вероятностью отказа этой системы. В этом случае, согласно уравнению (1-38), отказ любого элемента приводит к отказу системы.

Величины Р_ПР(t) и Q_ПР(t) являются соответственно надежностью и вероятностью отказа параллельного соединения элементов или системы с постоянным нагруженным резервом. В этом случае, согласно уравнению (1-40), при отказе одного элемента существует другой, который выполняет требуемую функцию и, следовательно, такая параллельная система из двух элементов не отказывает в работе, если отказал один элемент.

13. Сформулируйте условие минимума суммы квадратов отклонений для метода наименьших квадратов. Проиллюстрируйте выводы на примере.

для каждого значения экспериментальное и расчетное 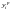значения различаются на некоторую величину , называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных разностей для всех точек была минимальной, найдем оптимальные параметры функции : если выполняется условие

(10.2)

где 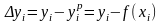, то считается, что функция подобрана наилучшим образом.

Линейная регрессия

Будем искать приближающую функцию в виде:

Абсолютная разность для определяется следующим образом:

формулу (10.2) перепишем в виде:

Рассматриваемая сумма является функцией с двумя параметрами Задача сводится к отысканию минимума этой функции. Используем необходимое условие экстремума:

т.е.

(10.3)

Решив систему двух уравнений с двумя неизвестными относительно параметров и , получим конкретный вид искомой функции Опуская математические выкладки, запишем выражения для искомых параметров:

(10.4)

Рассчитав значение , получим величину среднеквадратичной ошибки рассматриваемого приближения.