Теоретико-множественная интерпретация операций над событиями

Пусть проводится некоторый опыт со случайным исходом.

Множество Ω = {ω} всех возможных взаимоисключающих исходов данного опыта (испытания, эксперимента) называется пространством элементарных событий (коротко ПЭС), а сами исходы ω ‚ элементарными событиями (или «элементами», «точками»).

Случайным событием (или просто событием) называется любое подмножество множества Ω.

Элементарные события, входящие в подмножество А пространства Ω называются благоприятствующими событию А.

Множество Ω называется достоверным событием; ему благоприятствует любое элементарное событие, в результате опыта оно обязательно произойдет.

Пустое множество Ø называется невозможным событием; в результате опыта оно произойти не может.

Под операциями (действиями) над событиями понимаются операции над множествами, точнее – подмножествами пространства Ω.

Сумма (или объединение) двух событий А  Ω и В  Ω (обозначается А + В или А В) - это множество, которое состоит из элементов, принадлежащих хотя бы одному из событий А и В.

Произведение (или пересечение) двух событий А  Ω и В  Ω (обозначается А - В или А В) — это множество, которое состоит из элементов, общих для событий А и В.

Разность событий А  Ω и В  Ω (обозначается А — В или А \ В) — это множество, которое содержит те элементы события А, которые не входят в В.

Противоположным событию А  Ω называется событие Ā = О \ А; множество А называют также дополнением множества А.

Событие А влечет событие В (или А есть подмножество В), если каждый элемент события А содержится в В; обозначается А Í В

По определению Ø Í А для любого А

События А и В называются несовместными, если их произведение (пересечение) есть невозможное событие, т. е.

Несколько событий А₁, А₂, …, А_n образуют полную группу несовместных событий, если их сумма представляет все ПЭС, а сами события попарно не совместны т. е.

Полную группу, в частности, образуют события А и ( ).

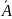Операции над событиями (множествами) обладают следующими свойствами:

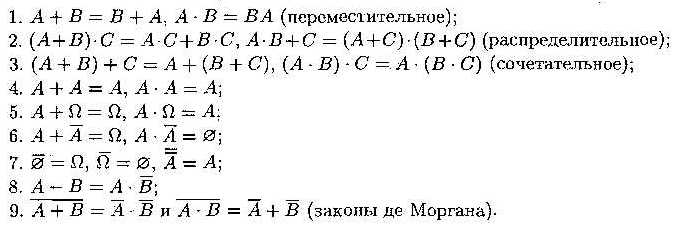
2.1. В урне находится 12 пронумерованных шаров. Опыт состоит в извлечении одного шара из урны. Требуется:

1) составить пространство элементарных событий для данного опыта;

2) указать элементарные события (исходы), благоприятствующие событиям: А={появление шара с нечетным номером), В = {появление шара с четным номером} С = {появление шара с номером большим, чем 3}, D = {появление шара с номером меньшим, чем 7);

3) пояснить, что означают события ;

4) указать, какие из пар событий А, В, С, D совместны а какие нет;

5) указать, какие из этих пар событий образуют полную группу, а какие нет;

6) привести примеры невозможного и достоверного событий;

7) принести пример другого пространства элементарных событий в данном опыте.

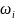О 1) Пространство элементарных событий можно записать в виде , где - появление шара с номером i, где i = 1,2,., 12. Появление i-го шара можно обозначить и так: Ш_i , и т.д. Поэтому можно записать:

2) Рассмотрим события А, В, С, и D как подмножества пространства Ω. Элементарные события входящие в эти подмножества и являются благоприятствующими указанным событиям:

, ,

,

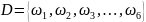
3) Событие означает, что событие В не происходит т.е. откуда ясно, что .

Событие 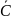является противоположным событию С, поэтому .

4) События А и В несовместны; события А и С, так же как А и D, В и С и другие совместны.

5) События А и В образуют полную группу и в результате опыта произойдет только одно из них: или А или В. Другие пары событий (А и С, В и D и т. д.) не образуют полную группу. Так, появление шара с номером 3 означает наступление двух событий: и А и В.

6) Событие Е₁ (появление шара с номером 13) является невозможным событием, а событие Е₂ = {появление шара с номером } достоверное т. е. Е₂ = Ω.

7) Если в данном опыте нас интересует лишь то, что извлеченный шар имеет четный или нечетный номер, то можно считать , где появление шара с нечетным номером, - с четным.

Другим возможным пространством для описания данного опыта может быть такое 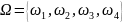, где появление шара с номером от 1 до 9 включительно, появление шара с номером 10, 11, 12 соответственно. Примером неправильно выбранного пространства может служить , где — появление шара с номером меньшим, чем 10, а – большем, чем 6. События и не являются элементарными, так как в результате опыта эти исходы могут наступить одновременно.

2.2. Указать пространства элементарных событий для следующих опытов (испытаний):

а) подбрасывание двух игральных костей;

б) стрельба по мишени до первого попадания;

в) наблюдение за временем безотказной работы прибора.

О а) Согласно правилу умножения (см. §1) число исходов в данном опыте равно 6 * 6 = 36. Изобразим пространство элементарных исходов (событий) в виде матрицы

где означает, что на первой игральной кости выпало i очков, а на второй j .

б) В данном случае пространство Ω теоретически бесконечно, но счетно. Обозначая знаком «+» попадание в цель при соответствующем выстреле, а знаком «-» промах получим такое пространство элементарных событий:

Ω={+, - +, - - +, - - - +, - - - - +, …}

Здесь, например, событие - - - + означает, что первые три выстрела были промахами, а на четвертый произошло попадание.

Можно записать ПЭС и так:

Ω = {1, 01 001, 0001,…},

где 1 означает попадание в цель, 0 - промах.

в) Здесь также исходов опыта (наблюдения) бесконечно много при этом множество Ω несчетное: , где — время безотказной работы прибора. Понятно, что в качестве результата наблюдения может появиться любое число .

2.3. Игральная кость бросается 1 раз. Описать пространство элементарных событий указать элементарные события, благоприятствующие событиям: А₁ — выпало четное число очков; А₂ — выпало не менее 4 очков; А₃ — выпало более 6 очков.

2.4. Построить пространство Ω для следующих испытаний:

а) проводится одна игра в шахматы;

б) трижды подбрасывается монета;

в) подсчитывается число студентов группы, давших экзамены по теории вероятностей.

2.5. Какие из следующих пар событий являются несовместными, совместными:

а) А₁ = {выход из строя телевизора, работающего в гостиной}, А₂ = {на кухне};

б) А₃ = {попадание при одном выстреле}, А₄ = {промах};

в) А₅ = {выпадение герба при бросании монеты}, А₆ = {выпадение решки},

г) А₇ = {хотя бы одно попадание при двух выстрелах} А₈ = {два попадания}?

2.6. Образуют ли полную группу следующие события:

а) А₃ и А₄ из задачи 2.5;

б) А₇ и А₈ из задачи 2.5;

в) В₀ = {ни одного попадания при трех выстрелах по мишени}, В₁ = {одно попадание}, В₂ = {два попадания}, В₃ = {три попадания};

г) С₁ = {покупатель купит товар хотя бы в одном из трех магазинов}, С₂ = {не купит ни в одном магазине}.

2.6. Каждый из двух стрелков производит по одному выстрелу в мишень. Пусть событие А = {первый стрелок попал в цель}, событие В = {второй стрелок попал в цель}. Что означают события:

а) А + В; б) А · B; в) ?

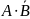О Составим пространство элементарных событий данного опыта: , где означает: первый стрелок промахнулся и второй промахнулся; первый попал, второй промахнулся и т.д. Тогда А = {(1-й стрелок попал, 2-й не попал) или (1-й стрелок попал, 2-й тоже попал)} =

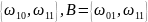
а) Событие А + В состоит в том, что хотя бы один стрелок попал в цель. Событие (множество) А + В состоит из элементарных исходов, каждый из которых входит или в множество А или в множество В, или в оба эти множества, т.е.

б) Событие А · B состоит в том, что оба стрелка попали в цель. Оно состоит из элементарных событий, каждое из которых входит и в множество А, и в множество В. Следовательно, А · B = .

в) Событие состоит в том, что первый стрелок попал в цель, а второй — нет. Оно состоит из тех элементарных событий каждое которых входит и в множество А и в множество , т.е. .

2.8. Три студента независимо друг от друга решают одну и ту задачу. Пусть событие А₁ - первый студент решил задачу, А₂ — второй студент решил задачу, А₃ — третий студент решил задачу. Выразить через события А_i (i = 1 2, 3) следующие события:

1) А = {все студенты решили задачу};

2) В = {задачу решил только первый студент);

3) С = {задачу решил хотя бы один студент};

4) В = {задачу решил только один студент},

О 1) Осуществление события А означает, что произошли события А₁, А₂ и А₃ одновременно, т. е. имеем произведение событий: А = А₁· А₂· А₃ .

2) В этом случае событие А произошло, а события А₂ и А₃ не произошли т. е. произошли события . Следовательно

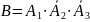
3) Событие С означает, что произошло или событие А₁ или событие А₂, или событие А₃, или любые два из них или все вместе, т. е. имеем сумму событий: С = А₁ + А₂ + А₃.

4) Задачу решит только первый студент 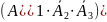, или только второй с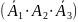тудент , или только третий студент 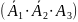, т. е. имеем сумму событий

.

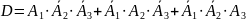2.9. Из корзины содержащей красные желтые и белые розы, выбирается один цветок. Пусть события А = {выбрана красная роза}, В = {выбрана желтая роза}, С = {выбрана белая роза}. Что означают события:

а) ; б) A + B; в) АС;

г) 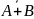д) ; е) АВ + C?

2.10. В задаче 2.8 найти выражения для следующих событий:

а) Е = {с задачей не справился ни один из студентов);

б) Р = {задачу решило не более двух студентов}.

2.11. В задаче 2.1 выяснить, что означают следующие события:

а) А + В; б) A·D; в)

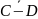
г) д) ; е)

2.12. Пусть А, В, С – три произвольных события. Выразить через А, В, С и их отрицания следующие события:

а) произошло только событие С; б) произошли все три события;

в) произошло по крайней мере одно из этих событий; г) произошло по крайней мере два события;

д) произошло только два события; е) ни одно событие не произошло;

ж) произошло не более двух событий.

2.13. Событие С влечет событие В. Что представляют собой события:

а) С + D, б) С·В, в) С—D; г) ?

2.14. Пусть событие А = {экзамен сдан}, а событие В = {сдан на отлично}. В чем состоят события:

а) А—В;

б) ;

в) ?

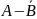2.15. Электрическая цепь составлена по схеме, приведенной на рисунке 1. Событие А_i = {элемент с номером i вышел из строя}, i = 1,2,3. Событие В = {схема вышла из строя (разрыв цепи)}. Выразить события В и через события А_i.

Рис. 1.

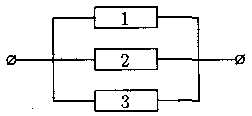Рис. 2.

2.16. Электрическая цепь составлена по схеме, приведенной на рисунке 2. Событие А₁ = {элемент с номером i вышел из строя}, i = 1,2,3. Событие В = {разрыв цепи}. Выразить события В и через события А_i.

2.17. Упростить выражение А + А · В.

О А + А · В = А · Ω + А · В = А (Ω + В) = А (В + Ω) = А · Ω = A, т.е. А + АВ = А. Использованы свойства 5, 2, 1 операций над событиями.