
- •§17.Определение производной
- •§34.Теорема Лагранжа
- •§35.Возрастание (убывание) функции
- •§36.Необходимые условия возрастания (убывания) функции
- •§37.Достаточные условия возрастания (убывания) функции
- •§38.Правило Лопиталя
- •§39.Формулы Тейлора и Маклорена
- •§40.Определение экстремума функции
- •§41.Необходимые условия экстремума функции
- •§42.Достаточные условия экстремума функции
- •§43.Выпуклость графика функции
- •§44.Необходимые условия выпуклости
- •§45.Достаточные условия выпуклости
- •§46.Определение точки перегиба
- •§47.Необходимые условия точки перегиба
- •§48.Достаточные условия точки перегиба
- •§49.Асимптоты
- •§50.План построения графиков
- •Формулы
§50.План построения графиков
Для построения графика рекомендуется определить:
1)область определения функции;
2)точки разрыва;
3)четность, нечетность функции;
4)периодичность функции:
5)точки пересечения с осями координат;
6)вертикальные асимптоты;
7)наклонные асимптоты;
8)определение экстремумов функции, интервалов возрастания и убывания функции;
9)определение точек перегиба и интервалов выпуклости.
Пример
50.1. Построим
график функции
![]() (рис.50.3).
(рис.50.3).
1)Функция определена
для всех
![]() .
.
2)При
![]() функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
3)Функция не
является четной и не является нечетной,
т.к.
![]() и
и
![]() .
.
4)Функция не является периодической.
5)Единственная
точка пересечения с осями координат
![]() .
.
6) Вертикальная асиптотоа , т.к. при функция равна бесконечности.
7)Найдем наклонную
асимптоту:
![]() =
=![]() =
=
=два раза правило Лопиталя=1,
![]() =
=![]() =самостоятельно=-3.
=самостоятельно=-3.
Наклонная асимптота
![]() .
.
8)![]() .
Критические точки:
.
Критические точки:
![]() ,
,
![]() ,
,
![]() .
Знаки первой производной указаны на
рис.50.1. Функция возрастает при
.
Знаки первой производной указаны на
рис.50.1. Функция возрастает при
![]() .
Убывает при
.
Убывает при
![]() (cм.
рис. 50.3).
(cм.
рис. 50.3).
9)
![]() .
Одна критическая точка
.
Знаки второй производной указаны на
рис.50.2. Функция выпукла вверх при
.
Одна критическая точка
.
Знаки второй производной указаны на
рис.50.2. Функция выпукла вверх при
![]() .
Выпукла вниз при
.
Выпукла вниз при
![]() .
.
![]()

Рис. 50.1. Рис. 50.2.

Рис. 50.3.
Пример 50.2. Построим график функции y=x-lnx.
1) Функция определена
при
![]()
2)Одна точка разрыва
(второго рода) при х=0. На множестве (0;+![]() функция непрерывна.
функция непрерывна.
3)Не является ни четной, ни нечетной (т.к. неопределена при отрицательных х).
4)Функция не является периодической.
5) Т.к.
![]() то график не пересекается с осью 0Х.
Т.к. при х=0 функция неопределена, то
график не пересекается с осью ОУ.
то график не пересекается с осью 0Х.
Т.к. при х=0 функция неопределена, то
график не пересекается с осью ОУ.
6)Т.к.
![]() 0-(
0-(![]() )=+
)=+![]() ,
то х=0 – вертикальная асимптота (см. рис.
50.5).
,
то х=0 – вертикальная асимптота (см. рис.
50.5).
7)Найдем наклонную асимптоту:
k=![]()
![]()
![]()
=правило
Лопиталя=![]()
![]() 1-0=1,
1-0=1,
![]() =
=![]()
![]() ,
т.к. не существует (конечного)
,
т.к. не существует (конечного)
![]() ,
то наклонной асимптоты нет.
,
то наклонной асимптоты нет.
8)Найдем производную:
![]()
![]() .
Определим критические точки:
.
Определим критические точки:
![]() при
при
![]()
![]() не существует при
не существует при
![]() .
.
Знаки первой производной на рис. 50.4. График функции на рис. 50.5.
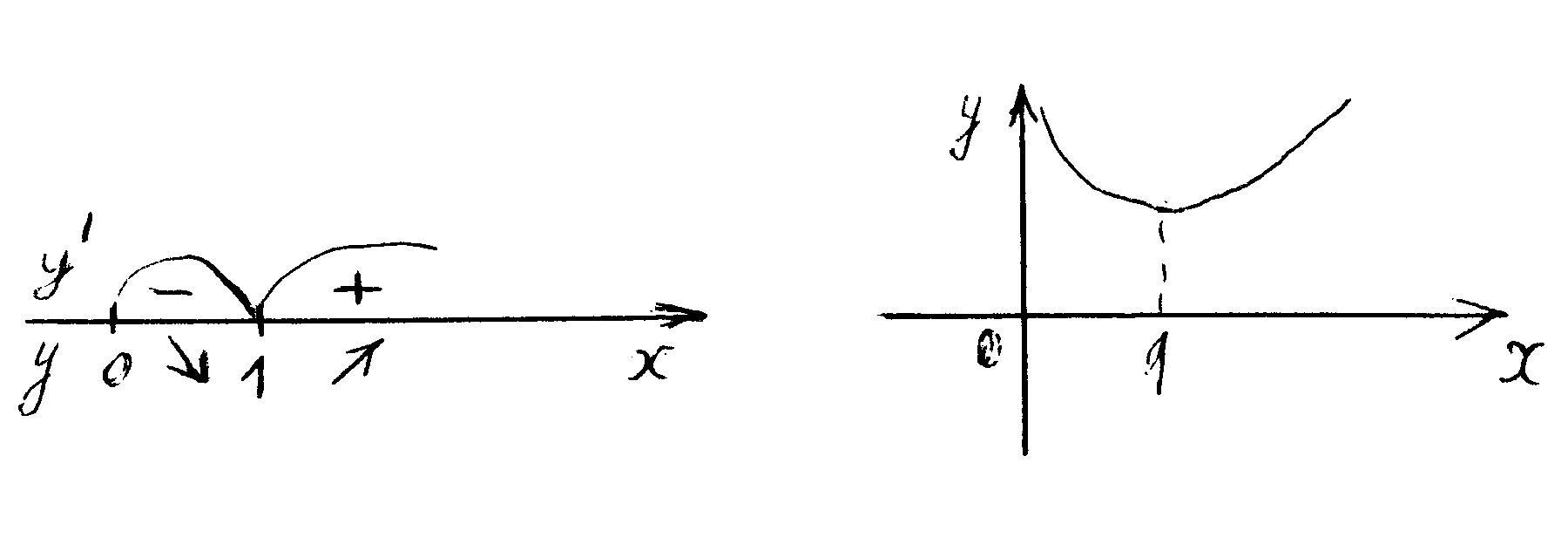
Рис. 50.4. Рис. 50.5.
9) Вторая производная
![]() >0 при x>0.
Поэтому функция выпукла вниз. График,
построенный на рис. 50.5 править (учитывая
вторую производную) не нужно.
>0 при x>0.
Поэтому функция выпукла вниз. График,
построенный на рис. 50.5 править (учитывая
вторую производную) не нужно.
Кстати
![]()
![]()
=Правило
Лопиталя=![]() что и отражено на рис. 50.5.
что и отражено на рис. 50.5.
Пример
50.3. Построим
график
![]()
1)Функция определена
при
![]()
2)При
![]() функция имеет разрыв второго рода.
функция имеет разрыв второго рода.
3)Функция не является ни четной, ни нечетной.
4)Функция не является периодической.
5)График пересекает ось 0Х при х=2, а ось 0У при у=-4/9.
6) Вертикальная асимптота х=-3.
7)Найдем наклонную
асимптоту:
![]() ,
,
![]() .
Прямая
.
Прямая
![]() является горизонтальной асимптотой.
является горизонтальной асимптотой.
8)Производная
(убедитесь самостоятельно)
![]() Критическая точка только
Критическая точка только
![]() Следовательно, экстремумов нет.
Следовательно, экстремумов нет.
Знаки первой
производной указаны на рис. 50.6, а график
см. рис.50.7.
Рис. 50.6. Рис. 50.7.
9)Вторая производная
![]() положительна при х<-3 и отрицательна
при x>-3,
что и указано на рис. 50.7.
положительна при х<-3 и отрицательна
при x>-3,
что и указано на рис. 50.7.
Пример
50.4. Приведем
полное исследование функции
![]()
1)Функция определена
при всех
![]() .
.
2)![]() - абсцисса точки разрыва.
- абсцисса точки разрыва.
3)Функция не является четной и не является нечетной.
4)Функция не является периодической.
5)График пересекает
оси ОХ и ОУ при
![]()
![]()
![]()
6)Вертикальная асимптота х=-1.
7)![]()
![]()
![]()
![]() Прямая
Прямая
![]() является наклонной асимптотой.
является наклонной асимптотой.
8)Убедитесь, что
производная:
![]() .
Критические точки:
.
Критические точки:
![]()
![]()
![]()
![]() Следующий рисунок показывает знаки
первой производной и график функции.
Точка с координатами
Следующий рисунок показывает знаки
первой производной и график функции.
Точка с координатами
![]() является
точкой максимума. 9)Убедитесь, что
является
точкой максимума. 9)Убедитесь, что
![]() Критические точки:
Критические точки:
![]() Функция
выпукла вверх, если
Функция
выпукла вверх, если
![]() т.е. при
т.е. при
![]() .
Функция выпукла вниз, если
.
Функция выпукла вниз, если
![]() т.е. при
т.е. при
![]() Следовательно,
точка
Следовательно,
точка
![]() является точкой перегиба.
является точкой перегиба.

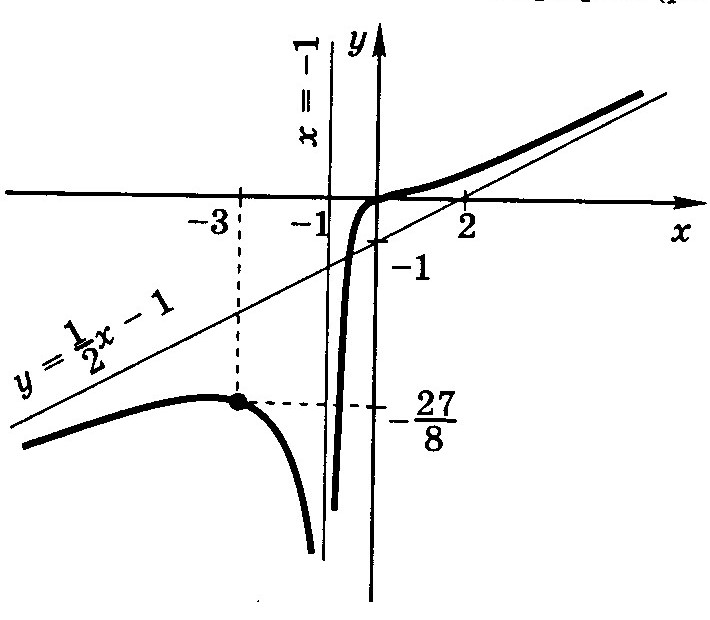
Рис. 50.8.
Вычислить пределы:
734![]() )
)
![]() .
-0,6
735)
.
-0,6
735)
![]() .
4
.
4
737)
![]() .
3/2
739)
.
3/2
739)![]() .
.
![]()
743)
![]() .
m/3
745)
.
m/3
745)
![]() .
-1/2
.
-1/2
747)
![]() .
0
749)
.
0
749)
![]() .
-2
.
-2
751)
![]() .
.
![]() 761)
761)
![]() .
-1/56
.
-1/56
764)
![]() . 1/3
768)
. 1/3
768)
![]() .
.
![]()
771)
![]() .
1/2
783)
.
1/2
783)
![]() .
1/2
.
1/2
Найти точки разрыва, указать их вид и построить графики функций:
814)у=![]() 815)у=
815)у=![]() 816)
816)
![]() ;
;


 817)у=
817)у=![]() 818)
818)
 ;
819)у=
;
819)у=![]()





820)![]() .
.
Вычислить пределы:
836)
![]()
![]()
![]()
838
)
![]() .
.
![]() 839
)
839
)
![]() .
.
![]() 840
)
840
)
![]() .
3
842
)
.
3
842
)
![]() .
1
.
1
842![]() )
)
![]()
![]()
![]()
Найти производные:
874
)
![]() 6cos6x
6cos6x
876
)
![]() .
.
![]()
881)
![]() .
.
![]()
886)
![]() .
.
![]()
888)
![]() .
.
![]()
896)
![]() .
.
![]()
937
)
![]() .
.
![]()
938
)
![]()
![]()
947
)
![]()
![]()
9ч50
)
![]() 951
)
951
)
![]()
![]()
952)
![]()
![]()
954)
![]()
![]()
956
)
![]()
![]()
957)
![]()
![]()
980)
![]()
![]() 983)
983)
![]() .
.![]()
985)
![]()
![]()
987
)
![]()
![]()
945)
![]()
![]()
981)
![]()
![]()
984)
![]()
![]()
1064
)
![]()
![]()
1067
)
![]()
![]()
Найти производные, используя (если можно) правило Лопиталя:
1122)
![]() 1126)
1126)
![]()
1127)
![]()
![]()
1130
)
![]() 1132)
1132)
![]()
![]()
1136)
![]() 1138)
1138)
![]()
![]()
Провести полное исследование функций:
1193)
![]() 1195)
1195)
![]() 1197)
1197)
![]()



1203)
![]() 1209)
1209)
![]() в промежутке
в промежутке
![]()
1254
)
![]() 1255
)
1255
)
![]()


