§34.Теорема Лагранжа

(франц. математик 1736-1813)

Теорема . Пусть функция определена и непрерывна на отрезке и дифференцируема в каждой точке интервала . Тогда существует точка такая, что

Пример 34.1. На рис. 34.1 дан график функции Рассмотрим участок графика между точками A(0;5) и В(2;9). Т.к. наша функция удовлетворяет условиям теоремы, то теорема Лагранжа утверждает, что на интервале найдется (по крайней мере одна) точка, через которую проведенная касательная параллельна прямой, проходящей через точки А и В.

Рис. 34.1.

§35.Возрастание (убывание) функции

Определение. Функция называется возрастающей на , если для любых точек , удовлетворяющих ,выполняется неравенство

Определение. Функция называется убывающей на , если для любых точек , удовлетворяющих , выполняется неравенство

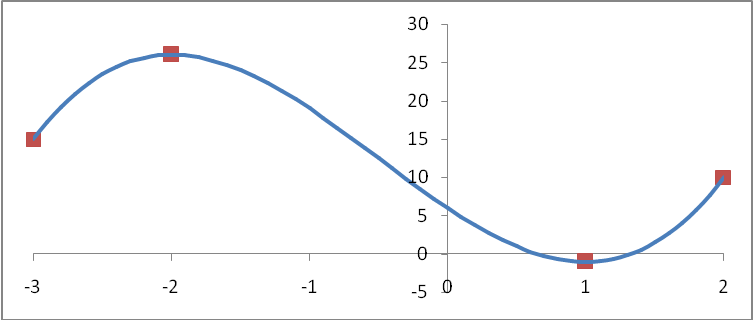
Рис. 35.1.

Пример 35.1. На рисунке 35.1 дан (на отрезке

[-3;2]) график функции Очевидно, что на отрезках [-3,-2] и [1,2] функция возрастает, а на отрезке [-2,1] убывает.

§36.Необходимые условия возрастания (убывания) функции

Теорема. Если функция дифференцируема и возрастает (убывает) на , то ( )

Пример 36.1. Функция, график которой указан на рис.36.1, возрастает на отрезке [-3,-2]. Поэтому тангенс угла наклона касательной (на этой части графика) не может быть отрицательным. При х=-2 тангенс угла наклона касательной равен нулю: (касательная горизонтальная, см. рис. 36.1).

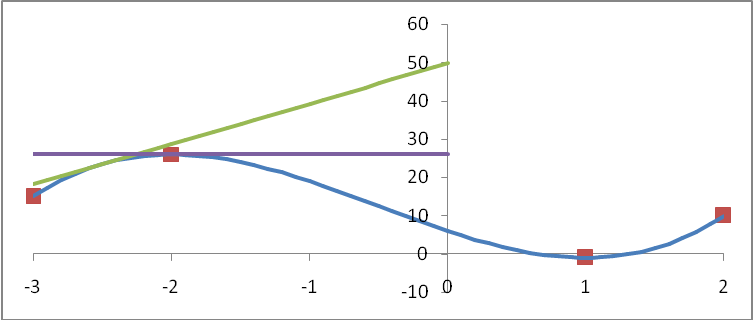
Рис. 36.1.

§37.Достаточные условия возрастания (убывания) функции

Теорема. Если ( ) то возрастает (убывает) на

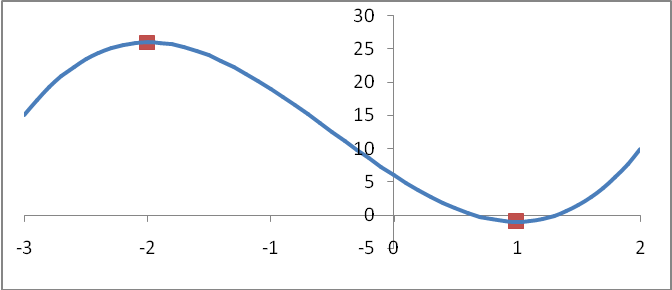
Рис. 37.1.

Пример 37.1. Рассмотрим (см. рис. 37.1) функцию Ее производная

Приравняем производную нулю Производная равна нулю при и (см. рис. 37.1, касательные в этих точках горизонтальные). На рис. 37.2 указаны знаки производной нашей функции. Пользуясь формулой замечаем, что производная положительна при и отрицательна при