МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования

В СЕРОССИЙСКИЙ
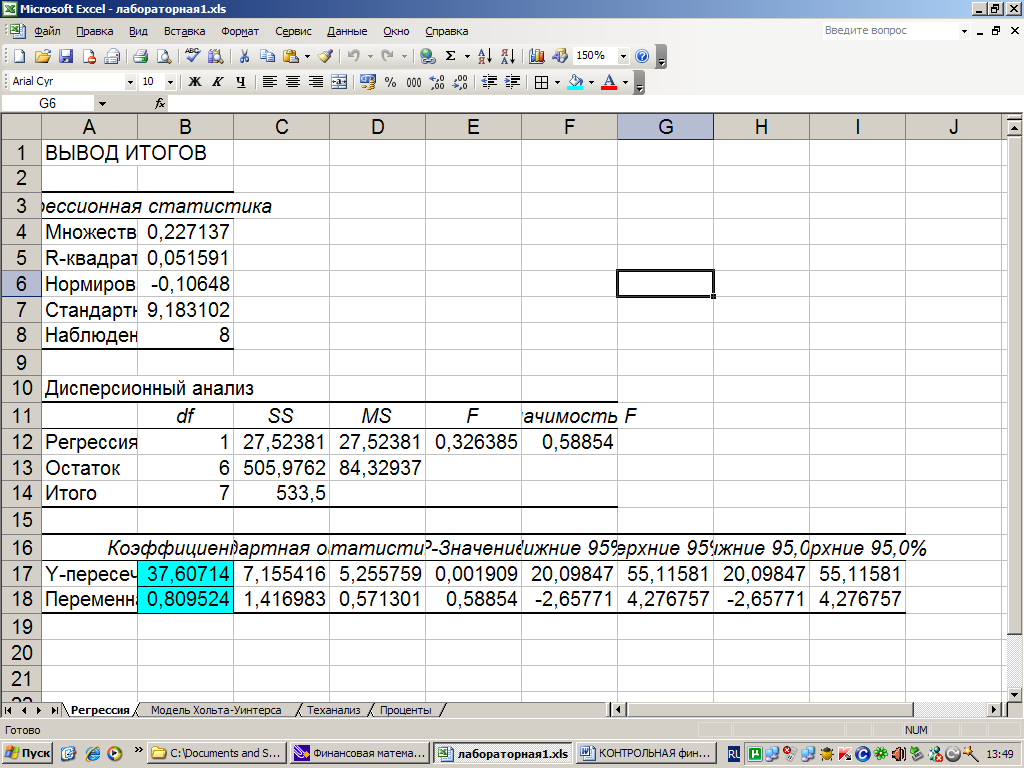
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
СЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Кафедра «Финансы и кредит» Контрольная работа по дисциплине: «Финансовая математика»
на тему: «Вариант №4»
Исполнитель:
Руководитель: Белолипцев И.И.
Уфа-2010
Содержание
Задача №1………………………………………………………………………….3
Задача №2………………………………………………………………………...15
Задача №3……………………………………………………………………..….27
Список использованной литературы…………………………………………...33
Задача 1
В каждом варианте приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).
квартал |
|
|
|
|
Вариант |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
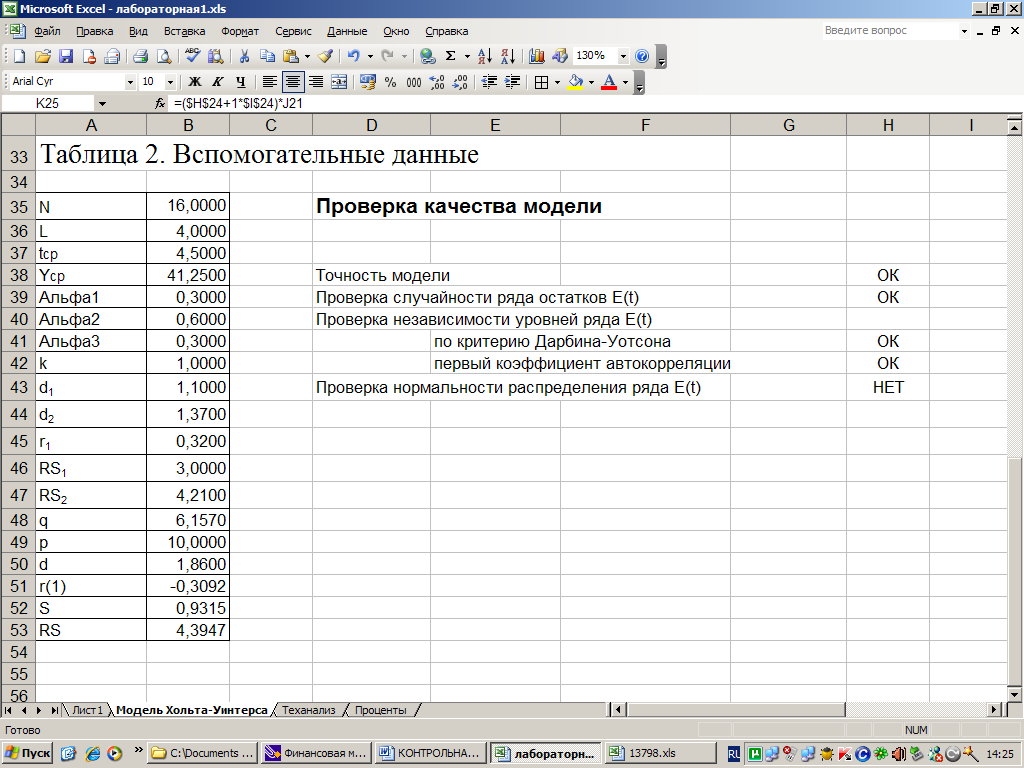
5 |
6 |
7 |
8 |
9 |
10 |
1 |
28 |
30 |
31 |
33 |
35 |
36 |
38 |
39 |
41 |
43 |
2 |
36 |
38 |
40 |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
3 |
43 |
45 |
47 |
50 |
52 |
55 |
57 |
59 |
62 |
64 |
4 |
28 |
30 |
31 |
33 |
34 |
35 |
37 |
38 |
40 |
41 |
5 |
31 |
32 |
34 |
36 |
37 |
39 |
40 |
42 |
44 |
45 |
6 |
40 |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
7 |
49 |
51 |
54 |
56 |
59 |
61 |
63 |
66 |
68 |
71 |
8 |
30 |
31 |
33 |
34 |
36 |
37 |
38 |
40 |
41 |
43 |
9 |
34 |
36 |
37 |
39 |
41 |
42 |
44 |
45 |
47 |
49 |
10 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
60 |
62 |
11 |
52 |
55 |
57 |
59 |
62 |
64 |
67 |
69 |
71 |
74 |
12 |
33 |
34 |
35 |
37 |
38 |
40 |
41 |
42 |
44 |
45 |
13 |
39 |
41 |
42 |
44 |
46 |
47 |
49 |
50 |
52 |
54 |
14 |
48 |
50 |
52 |
54 |
56 |
58 |
60 |
62 |
64 |
66 |
15 |
58 |
60 |
62 |
65 |
67 |
70 |
72 |
74 |
77 |
79 |
16 |
36 |
37 |
39 |
40 |
41 |
43 |
44 |
46 |
47 |
48 |
Требуется.
Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания
 .
.Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.
Оценить адекватность построенной модели на основе исследования:
случайности остаточной компоненты по критерию пиков;
независимости уровней ряда остатков по d-критерию (критические значения
 и
и
 )
и по первому коэффициенту автокорреляции
при критическом значении
)
и по первому коэффициенту автокорреляции
при критическом значении
 ;
;нормального распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
Построить точечный прогноз на 4 шага вперед, т.е. на один год.
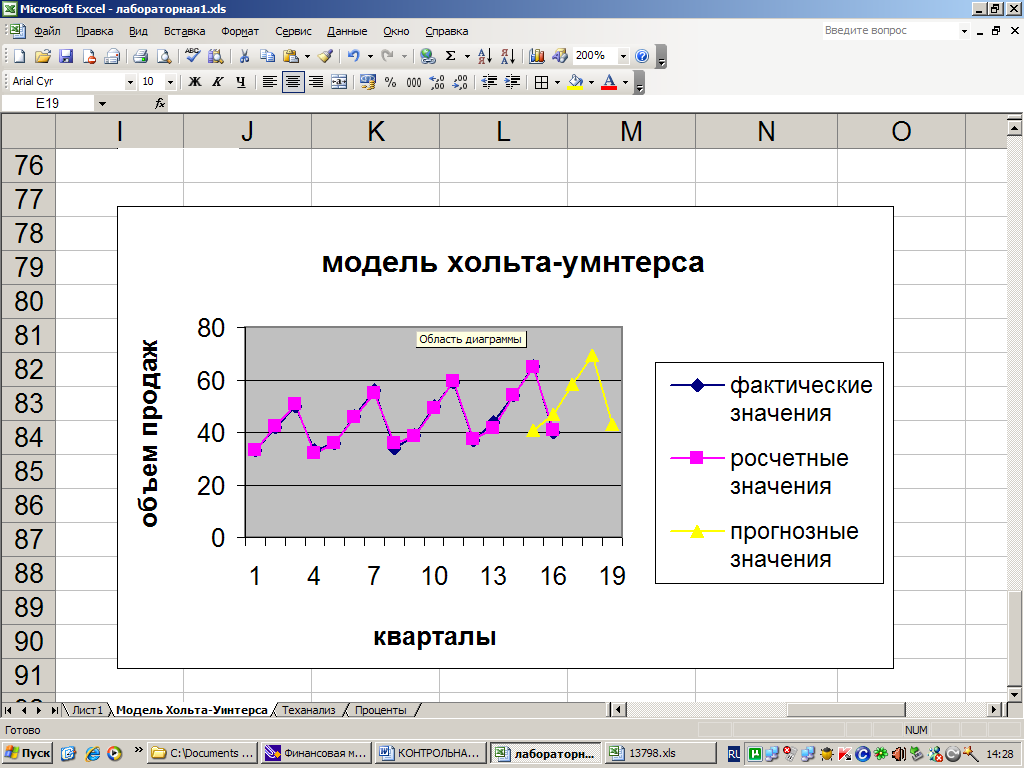
Отразить на графике фактические, расчетные и прогнозные данные.
Решение.
Основная формула модели Хольта-Уинтерса имеет вид
![]()
Здесь k – период упреждения;
![]() – расчетное значение показателя для
(t+k)
–го периода;
– расчетное значение показателя для
(t+k)
–го периода;
![]() – коэффициенты модели;
– коэффициенты модели;
L – период сезонности (для квартальных данных L=4);
![]() – прошлогодний коэффициент сезонности
того периода, для которого рассчитывается
показатель.
– прошлогодний коэффициент сезонности
того периода, для которого рассчитывается
показатель.
Коэффициенты
модели
![]() уточняются (адаптируются) при переходе
от уровня t-1
к новому значению t.
Это уточнение производится по формулам:
уточняются (адаптируются) при переходе
от уровня t-1
к новому значению t.
Это уточнение производится по формулам:
![]() ;
;
![]() ;
;
![]() .
.
Здесь
![]() - параметры сглаживания.
- параметры сглаживания.
Для проведения
вычислений по формулам Хольта необходимо
знать начальные оценки
![]() коэффициентов модели для последнего
квартала предыдущего года, а также
коэффициенты сезонности
коэффициентов модели для последнего
квартала предыдущего года, а также
коэффициенты сезонности
![]() за весь предыдущий год
за весь предыдущий год
Зарезервируем для
этих величин дополнительно 4 уровня
![]() в расчетной таблице и выполним
предварительный расчет.
в расчетной таблице и выполним
предварительный расчет.
С помощью метода наименьших квадратов
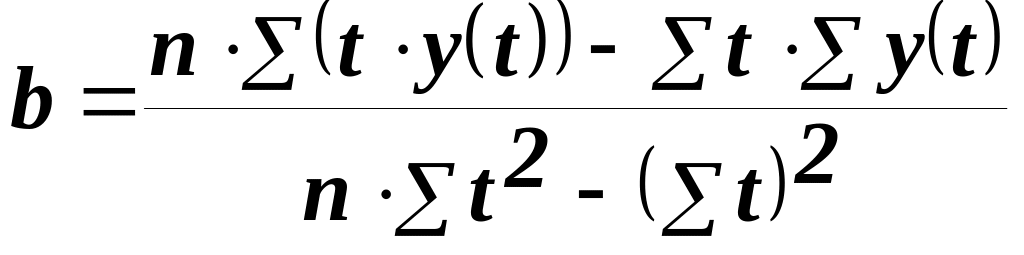
![]()
построим
вспомогательную линейную модель
![]() .
Коэффициенты этой модели
.
Коэффициенты этой модели
![]() можно получить с помощью «мастер
функций/ статистические/ ЛИНЕЙН» или
«сервис/ анализ данных/ РЕГРЕССИЯ».
можно получить с помощью «мастер
функций/ статистические/ ЛИНЕЙН» или
«сервис/ анализ данных/ РЕГРЕССИЯ».
Уравнение вспомогательной линейной модели запишется в виде
![]() .
.
Примем
![]() ,
,
![]() ,
занесем эти значения в нулевой уровень
соответствующих столбцов основной
расчетной таблицы.
,
занесем эти значения в нулевой уровень
соответствующих столбцов основной
расчетной таблицы.
Для оценки
коэффициентов сезонности
найдем с помощью вспомогательной модели
расчетные значения
![]() для
для
![]() и сопоставим их с фактическими
и сопоставим их с фактическими
Коэффициент сезонности – это отношение фактического значения показателя к значению, найденному по линейной модели.
Для первого квартала
это
![]() в первом году и
в первом году и
![]() во втором году. В качестве окончательной
(более точной) оценки коэффициента
сезонности
во втором году. В качестве окончательной
(более точной) оценки коэффициента
сезонности
![]() первого квартала предыдущего года
возьмем среднее арифметическое значение
первого квартала предыдущего года
возьмем среднее арифметическое значение
![]() .
.
Аналогично найдем
![]() ,
,
![]() ,
,
![]() .
.
Полученные значения занесем в соответствующие уровни столбца «F» основной расчетной таблицы.
Перейдем к построению собственно модели Хольта.
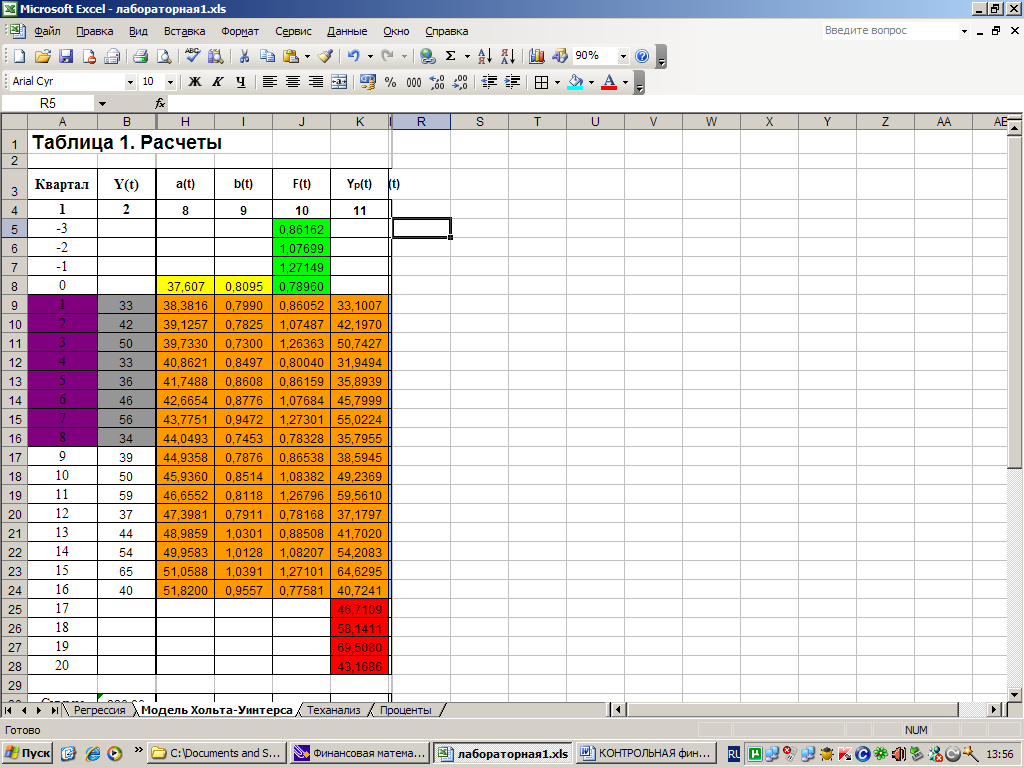
Согласно условию
задачи коэффициенты сглаживания
;
период сезонности
![]() .
.
По основной формуле
модели Хольта-Уинтерса, приняв
![]() ,
рассчитаем начальное значение
,
рассчитаем начальное значение
![]()
![]() .
.
Теперь перейдем
к
![]() и уточним коэффициенты модели
и уточним коэффициенты модели
![]() ;
;
![]() ;
;
![]() .
.
По основной формуле
модели Хольта-Уинтерса при
![]() получим
получим
![]() .
.
Перейдем к
![]() и уточним коэффициенты модели
и уточним коэффициенты модели
![]() ;
;
![]() ;
;
![]() .
.
По основной формуле модели Хольта при получим
![]()
и т.д. для
![]() .
Максимальное значение t,
для которого могут быть рассчитаны
коэффициенты
,
определяется количеством исходных
данных и равно 16.
.
Максимальное значение t,
для которого могут быть рассчитаны
коэффициенты
,
определяется количеством исходных
данных и равно 16.
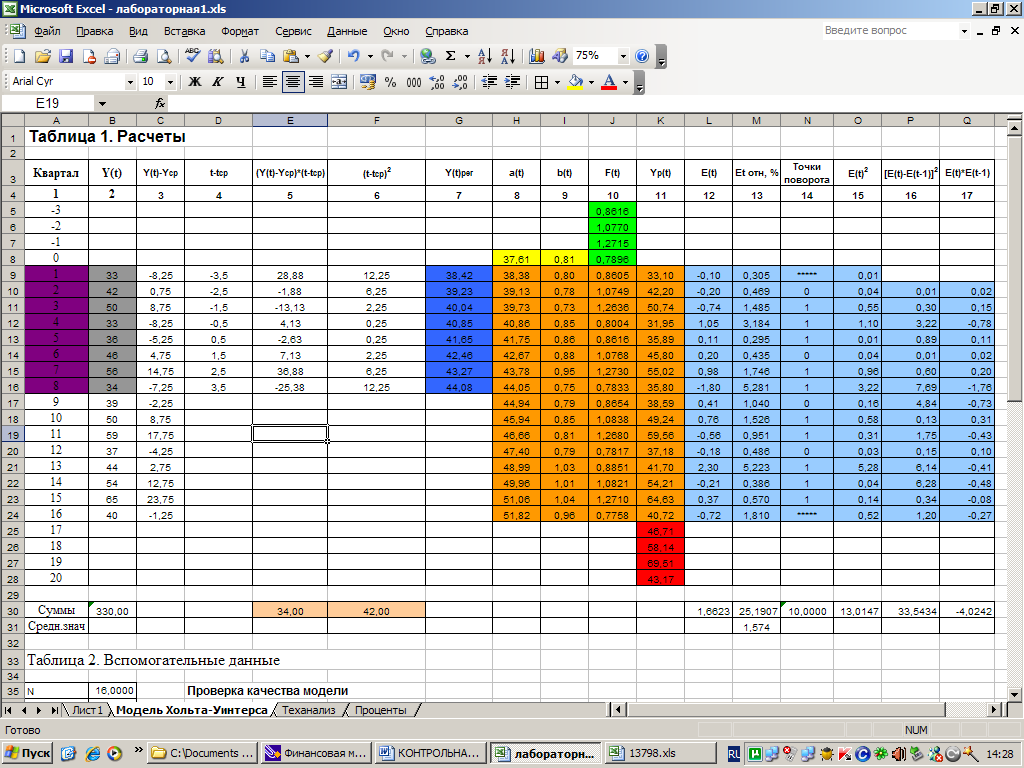
Результаты вычислений приведены в основной расчетной таблице.
Таким образом, модель Хольта-Уинтерса построена.
Оценим точность построенной модели.
Предварительно
для каждого уровня исходных данных
вычислим остатки
![]() и относительные погрешности
и относительные погрешности
![]() ;
затем определим среднюю относительную
ошибку аппроксимации
;
затем определим среднюю относительную
ошибку аппроксимации
![]() .
.
Вывод о точности
модели делают на основании расчета
средней относительной погрешности
аппроксимации
![]() согласно схеме:
согласно схеме:
точная удовлетв. неудовл.
![]()
0 5% 15%
если
 ,
говорят о высокой точности модели;
,
говорят о высокой точности модели;если
 ,
точность модели считают удовлетворительной;
,
точность модели считают удовлетворительной;если
 ,
точность модели неудовлетворительная.
,
точность модели неудовлетворительная.
Дополним расчетную
таблицу столбцом
![]() :
:

Средняя относительная погрешность аппроксимации составит
![]() (%) .
(%) .
Следовательно, относительная ошибка аппроксимации равна 1,57 %, она не превышает 5%, что позволяет сделать вывод о высокой точности модели.
Модель считается
адекватной, если для ряда остатков
![]() выполняются следующие свойства:
выполняются следующие свойства:
равенство нулю математического ожидания;
случайности;
независимости;
нормального распределения
Для проверки используем критерий Стъюдента, согласно которому
Вычисляем t-статистику
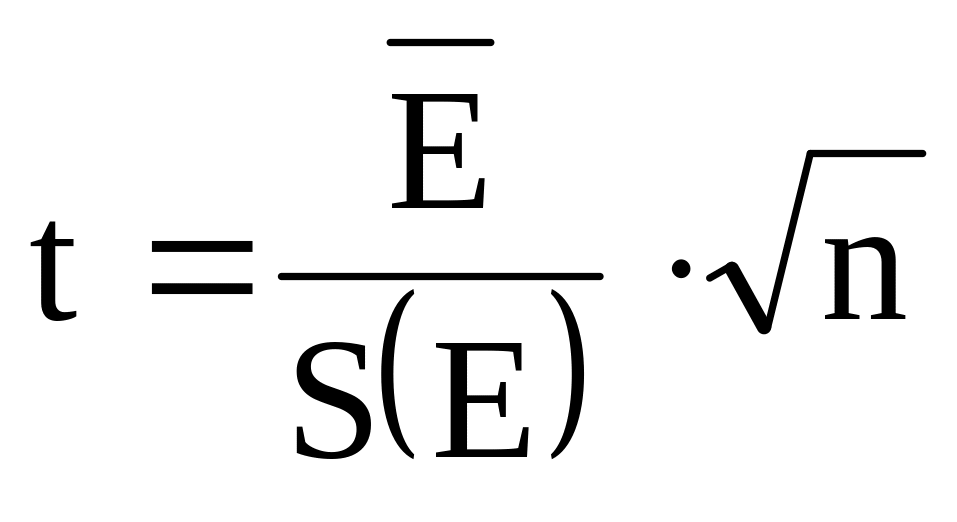 ,
t=
0.449175
,
t=
0.449175
где
![]() - среднее значение
остаточной компоненты;
- среднее значение
остаточной компоненты;
![]() - среднее квадратичное
отклонение для ряда остатков.
- среднее квадратичное
отклонение для ряда остатков.
Сравниваем полученную фактическую величину с критическим значением
 .
.
При n=16 критическое значение tкр.=2,13
Делаем вывод согласно схеме:
не вып. вып. не вып.
![]()
![]() 0
t
0
t
если
 ,
то отличие
от нуля является незначимым, случайным,
проверяемое свойство выполняется;
,
то отличие
от нуля является незначимым, случайным,
проверяемое свойство выполняется;если
 ,
то отличие
от нуля является значимым, закономерным,
проверяемое свойство не выполняется,
модель неадекватна.
,
то отличие
от нуля является значимым, закономерным,
проверяемое свойство не выполняется,
модель неадекватна.
Следовательно, 0,449175 < 2.13 отличие от нуля является незначимым, случайным, проверяемое свойство выполняется.
Для проверки используем критерий поворотных точек, в соответствии с которым
Подсчитываем фактическое количество р поворотных точек для ряда остатков E(t).
Критическое значение определяем по формуле
![]() ,
,
где
![]() - количество уровней ряда,
- количество уровней ряда,
квадратные скобки в формуле означают целую часть числа.
Сравниваем значения p и pкр и делаем вывод согласно схеме:
не вып. вып.
![]()
0 pкр p
если
 ,
то свойство случайности уровней ряда
остатков выполняется;
,
то свойство случайности уровней ряда
остатков выполняется;
если
![]() ,
то ряд остатков нельзя считать случайным,
он содержит регулярную компоненту,
следовательно, модель не является
адекватной.
,
то ряд остатков нельзя считать случайным,
он содержит регулярную компоненту,
следовательно, модель не является
адекватной.
Подсчитаем количество поворотных точек, их количество равно 10. Ркр.=6. Сравнивая значения, можно прийти к выводу, что свойство случайности уровней ряда остатков выполняется.
Проверку проводим по критерию Дарбина-Уотсона.
Вычисляем статистику
 .
.
Сравниваем полученную фактическую величину d с критическими уровнями d1 и d2.
Делаем вывод согласно схеме:
не вып. доп.пр.
вып.
![]()
![]()
0 d1 d2 2 4 d
если
 ,
то уровни ряда остатков сильно
автокоррелированы, модель неадекватна;
,
то уровни ряда остатков сильно
автокоррелированы, модель неадекватна;если
 ,
то однозначного вывода о зависимости
или независимости уровней ряда остатков
по критерию Дарбина-Уотсона сделать
нельзя, требуется дополнительная
проверка;
,
то однозначного вывода о зависимости
или независимости уровней ряда остатков
по критерию Дарбина-Уотсона сделать
нельзя, требуется дополнительная
проверка;если
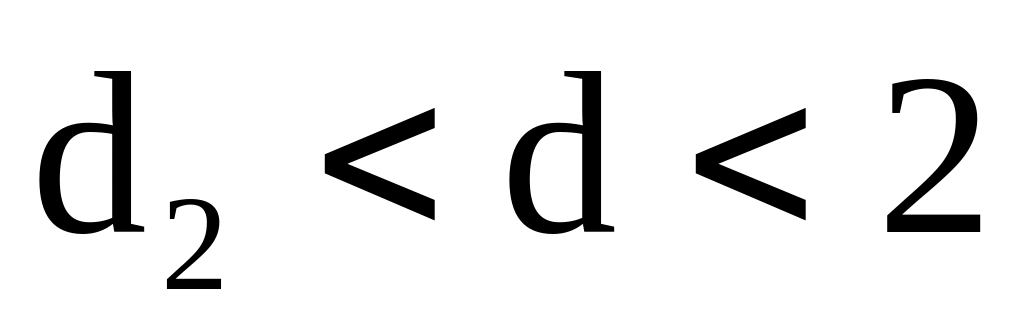 ,
то уровни ряда остатков являются
независимыми;
,
то уровни ряда остатков являются
независимыми;
- если
![]() ,
то это свидетельствует об отрицательной
корреляции.
,
то это свидетельствует об отрицательной
корреляции.
В этом случае перед проверкой величину d следует заменить на .
С помощью функций «СУММКВ» и «СУММКВРАЗН» найдем
![]() ,
,
![]() .
.
Таким образом,
![]() .
.
При
![]() критические значения d
– статистик
критические значения d
– статистик
![]() .
.
2 < d < 4, => = 4-2.58=1.42
Выполним дополнительную проверку с помощью первого коэффициента автокорреляции.
Вычислим первый коэффициент автокорреляции
 .
.
Сравним полученную фактическую величину
 с критическим
значением
с критическим
значением
 .
.
Делаем вывод согласно схеме:
вып. не вып.
![]()
0
![]()
если
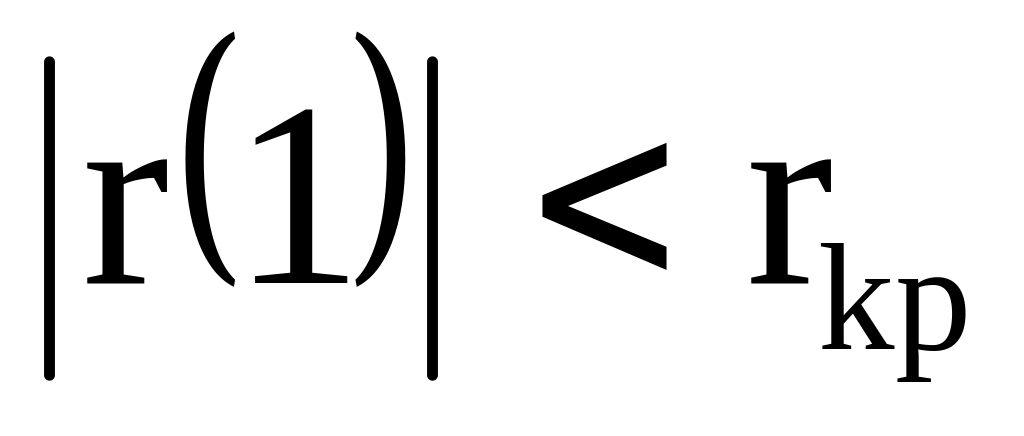 ,
то свойство независимости остаточной
компоненты выполняется;
,
то свойство независимости остаточной
компоненты выполняется;если
 ,
то наблюдается существенная автокорреляция
уровней ряда остатков, модель неадекватна.
,
то наблюдается существенная автокорреляция
уровней ряда остатков, модель неадекватна.
r(1)= |
-0,30919 |
Следовательно, свойство независимости остаточной компоненты выполняется, т.к. rкр.=0,32
Для проверки соответствия ряда остатков нормальному закону распределения используется R/S критерий.
Вычисляем статистику
 =
4,395,
=
4,395,
где
![]() - максимальный уровень ряда остатков;
- максимальный уровень ряда остатков;
![]() -
минимальный уровень ряда остатков;
-
минимальный уровень ряда остатков;
- среднее квадратичное отклонение уровней ряда остатков.
Сопоставляем полученную фактическую величину R/S с критическим интервалом.
Делаем вывод согласно схеме:
не вып. вып. не вып.
![]()
критич. инт-л R/S
если
 критическому
интервалу, то гипотеза о нормальном
распределении уровней ряда остатков
принимается;
критическому
интервалу, то гипотеза о нормальном
распределении уровней ряда остатков
принимается;если
 критическому
интервалу, то уровни ряда остатков не
подчиняются нормальному распределению,
модель неадекватна.
критическому
интервалу, то уровни ряда остатков не
подчиняются нормальному распределению,
модель неадекватна.
Критические значения от 3 до 4,21, следовательно, уровни ряда остатков не подчиняются нормальному распределению, модель неадекватна
Составим с помощью построенной модели прогноз на один год вперед.
Для первого квартала
будущего пятого года положим в основной
формуле модели Хольта-Уинтерса
![]() и найдем
и найдем
![]() .
.
Для второго квартала
будущего пятого года при
![]() найдем
найдем
![]()
Для третьего
квартала будущего пятого года при
![]() найдем
найдем
![]() .
.
Для четвертого
квартала будущего пятого года при
![]() найдем
найдем
![]() .
.
Исходные данные и результаты всех выполненных расчетов покажем на общем графике.