II. 6. Покажите и объясните дифракцию на одной щели (дифракция Фраунгофера).

Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 4.8, а).

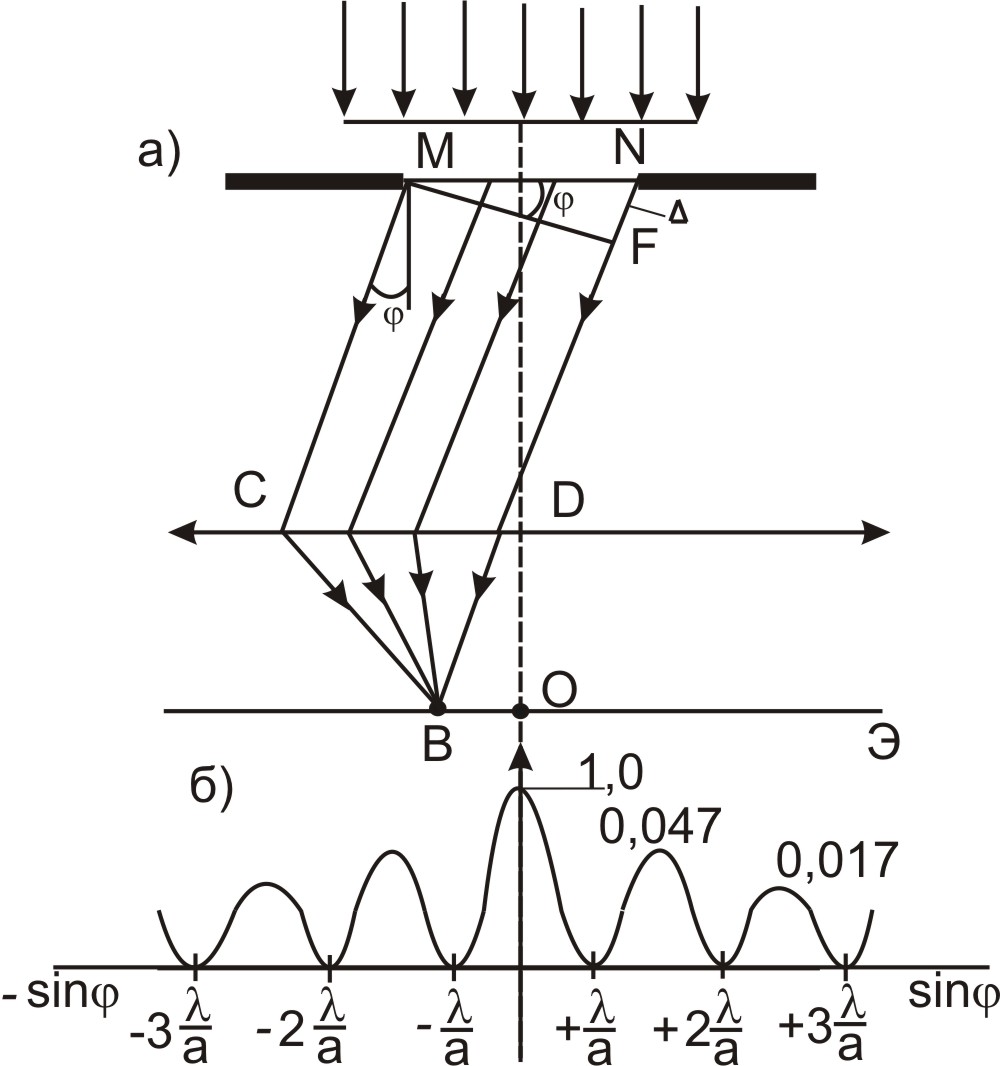
Рис. 4.8

Оптическая разность хода между крайними лучами МС и ND , идущими от щели в произвольном направлении φ,

∆ = NF = α sin φ,

где F – основание перпендикуляра, опущенного из точки М на луч ND.

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уместится ∆: λ/2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одной фазе. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля, укладывающихся на ширине щели, зависит от угла φ. От числа зон Френеля в свою очередь зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то

(m = 1, 2, 3, …) (4.6)

и в точке В наблюдается дифракционный минимум ( полная темнота), если же число зон Френеля нечетное, то

(m = 1, 2, 3, …) (4.7)

и наблюдается дифракционный максимум, соответствующий действию одной некомпенсированной зоны Френеля. Отметим, что в направлении φ = 0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью, т.е. в точке О наблюдается центральный дифракционный максимум (рис. 4.8 б).

II. 7. Объясните метод определения длины световой волны в лабораторной работе.

Пусть плоская световая волна длиной λ. падает нормально на решетку. За щелями в результате дифракции лучи будут распространяться в различных направлениях. Рассмотрим лучи, составляющие угол с первоначальным их направлением. Очевидно, что лучи, идущие от соответственных точек решетки, будут когерентными и разность хода лучей 1 и 1' составит

(7.1)

Этой разности хода будет соответствовать разность фаз между этими лучами

, (7.2)

Как известно, если , то , т.е. лучи 1 и 1', если их наложить друг на друга, будут приходить в точку сведения в одинаковых фазах и, следовательно, должны усилить друг друга. Условие образования интерференционного максимума имеет вид:

,

Максимумы, удовлетворяющие этому условию, называются главными максимумами. При m=0, и на экране после дифракционной решетки получим дифракционный максимум, называемый нулевым (или центральным). При m=1 симметрично по обе стороны от центрального максимума возникает два дифракционных максимума 1-го порядка и т.д. При освещении дифракционной решетки естественным белым светом на экране вместо светлых полос будут видны спектры, разделенные темными промежутками (как известно, спектр радужных полос расположен между красным светом, длина волны которой , и фиолетовым - ). Значит, положение максимума зависит от длин волны .

Каждый максимум смещен от положения центрального максимума на некоторое расстояние . Угол, на который будут отклоняться лучи от первоначального направления при прохождении дифракционной решетки, можно рассчитать по формуле

где l - расстояние от дифракционной решетки до экрана, на котором наблюдают интерференционную картину.

Для проведения исследования используется оптическая скамья, на которой установлены: осветитель 1, диафрагма 2 в виде щели, светофильтр 3, дифракционная решетка 4 , собирающая линза 5, матовый экран 6. Все установленные на скамье принадлежности могут свободно перемещаться как по горизонтали, так и по вертикали, а расстояние между ними измеряется линейкой, закрепленной на оптической скамье. Расстояние между световыми максимумами определяется по шкале, установленной на экране.

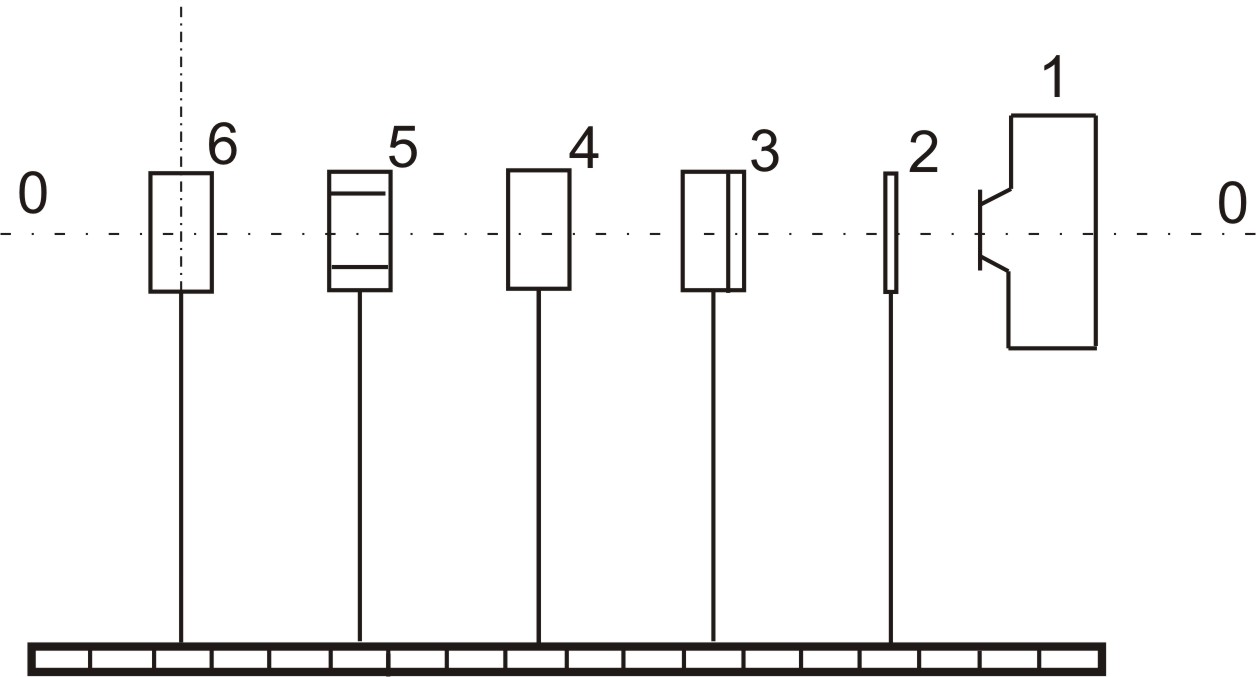
Рис. 4.9

Учитывая, что углы между лучами главного максимума и лучами, образующими боковые максимумы, малы будем считать, что .

Тогда

(4.8)

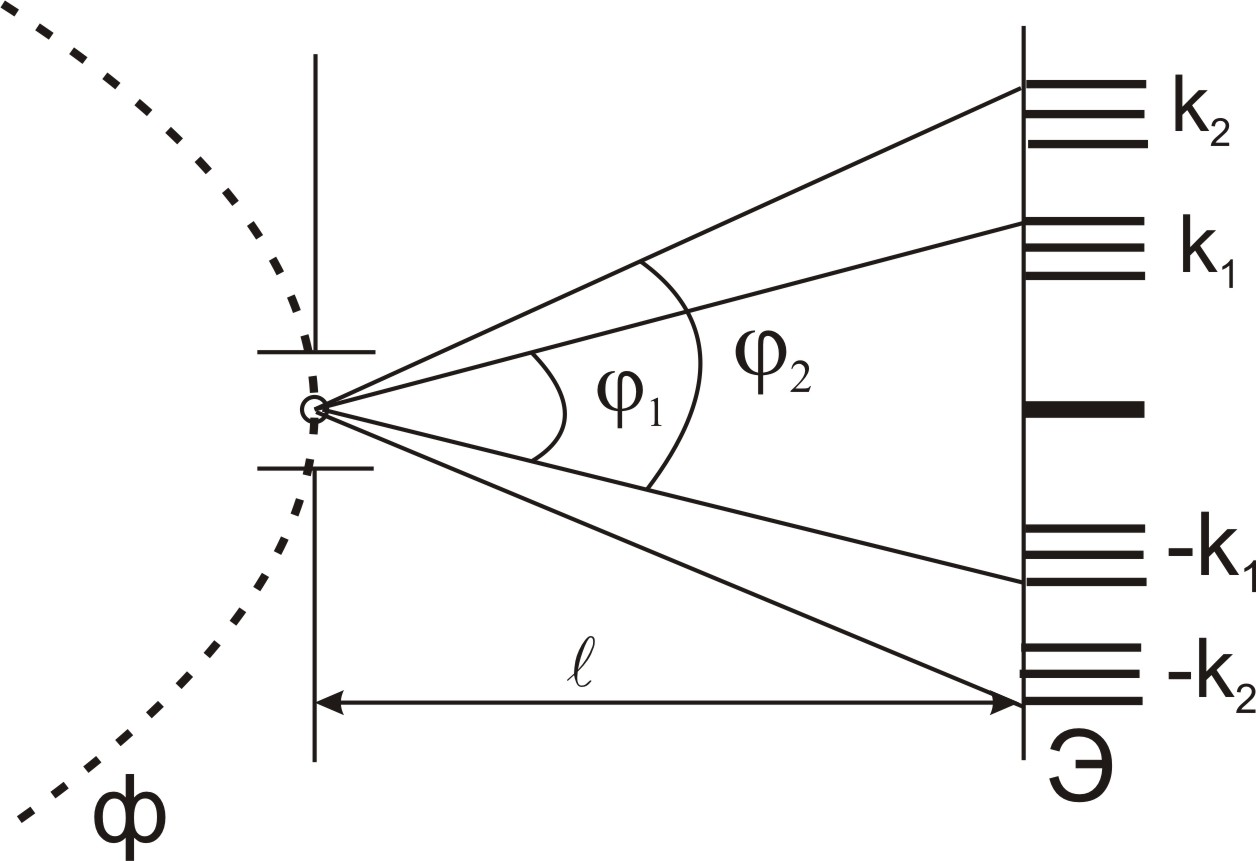
Рис. 4.10