II. 17. Объясните физическую сущность определения скорости звука методом резонанса.
Для определения длины звуковой волны, излучаемой генератором звука, используют стоячие волны, которые образуются в открытой стеклянной трубке, второй конец которой закрыт подвижной, более плотной перегородкой. Если у открытого конца трубки поместить телефон, соединенный с генератором звуковых колебаний, то колебания его мембраны будут передаваться воздушному столбу в трубке. Возникшая таким образом звуковая волна будет распространяться в воздухе, достигнув преграды, отразится от нее и, изменив при этом фазу на противоположную, пойдет навстречу бегущей волне.
Рис. 3.7
Бегущая и отраженная волны, интерферируя, образуют стоячую волну и волновой процесс в среде будет описываться уравнением
где
А - амплитуда бегущей волны;
- частота колебаний;
- длина бегущей
волны; t
– время.
Графически стоячая волна может быть изображена так, как показано на рис.3.8.
Рис. 3.8.
График стоячей волны. Смещение точек среды от положения равновесия: а - в некоторый момент (сплошная линия); б - через четверть периода (пунктирная линия)
Одна
из характерных особенностей стоячей
волны состоит в том, что в ней амплитуды
колебаний точек различны в различных
местах среды и согласно уравнению (3.8)
остаются неизменными, а следовательно,
имеются
узлы и пучности колебаний. В бегущей
волне амплитуды везде одинаковы.
Расстояние между соседними узлами (или
пучностями) называют длиной стоячей
волны. Оно
равно половине длины бегущей волны
(
).
В случае образования стоячей волны в некоторой среде, имеющей ограниченные размеры, (например, столб воздуха в трубке) интерференцией прямой и обратной волны, отраженной от более плотной среды, на границе воздушного столба с преградой образуется узел. Как и любая колебательная система, столб воздуха в трубке обладает собственными колебаниями. В данном случае собственными колебаниями столба воздуха в трубке являются стоячие волны. При этом между длиной l столба воздуха и длиной стоячей волны в нем должно выполняться соотношение
,
m=1,2,3...
т.е. когда во всей длине l столба будет укладываться целое число длин волн стоячей волны (или полуволн бегущей волны), то можно говорить о собственной частоте колебаний воздушного столба, заключенного в трубке. Поскольку длинам волн бегущей волны, создающей стоячую волну в трубке
,
m=1,2,3…
соответствуют частоты
,
m=1,2,3…
которые
совпадают с собственными частотами
колебаний системы (где U
- скорость распространения звука в
воздухе), то говорят, что
имеет место явление резонанса. Наименьшая
из этих частот будет соответствовать
наибольшей длине волны
.
III. Задачи
1. Шарик (материальная точка) массой m совершает гармонические колебания с амплитудой А на пружине с жесткостью k. На расстоянии A/2 от положения равновесия установили массивную стальную плиту, от которой шарик абсолютно упруго отскакивает. Найти период колебания в этом случае.
Рис. 3.9
2. Шарик массой m с зарядом q > 0 подвешен на тонкой нити внутри плоского конденсатора с горизонтально ориентированными пластинами. Напряженность поля конденсатора равна Е, силовые линии направлены вниз. Найти период колебаний такого маятника. Длина нити равна l. Как изменится формула для периода, если изменить знак заряда на пластинах конденсатора ?
3. Математический маятник длиной l совершает колебания вблизи вертикальной стенки. Под точкой подвеса маятника на расстоянии l= l/2 от нее в стенку забит гвоздь. Найти период колебаний маятника Т.
Рис. 3.10
На идеально гладкой горизонтальной плоскости расположен брусок массой Μ=1 кг, закрепленный пружинами, жесткость каждой из которых k=30 Н/м. На бруске лежит шайба массой m=0,5 кг. Система брусок - шайба приводится в колебательное движение. Определить максимальную амплитуду колебаний, при которой система будет двигаться как единое целое, т. е. без проскальзывания шайбы по бруску. Коэффициент трения скольжения между бруском и шайбой μ = 0,4.
Рис. 3.11
На горизонтальной пружине укреплено тело массой 10 кг, лежащее на абсолютно гладком столе. В это тело попадает и застревает в нем пуля массой т =10 г, летящая со скоростью V=500 м/с по направлению вдоль оси пружины. Амплитуда возникших при этом колебаний А =0,1 м. Найти период колебаний.
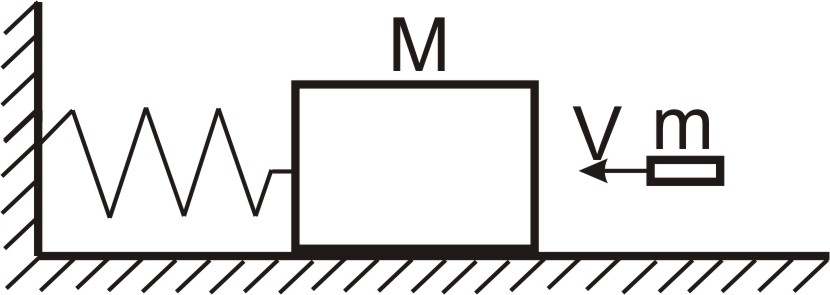
Рис. 3.12
На вертикально расположенной пружине с коэффициентом жесткости k подвешен груз массой т. Грузу сообщают начальную скорость V, направленную вертикально вниз. Определить период и амплитуду колебаний груза.
Точка совершает колебания по закону
,
где А
= 4 см.
Определить начальную фазу
,
если: 1) х(0)
= 2 см и х
(0) < 0;
2) х(0)
=
см и
х(0)
> 0; 3) х(0)
= -
см
и х(0)
< 0; 4) х(0)
= -
см и x(0)
> 0. Построить векторную диаграмму для
момента t
= 0.Точка совершает колебания по закону
,
где А
= 2 см; ω
= π с-1;
φ
= π/4 рад.
Построить графики зависимости от
времени: 1) смещения
;
2)
скорости
;
3)
ускорения
.Определить максимальные значения скорости
и
ускорения
точки, совершающей гармонические
колебания с амплитудой А=
3 см и циклической частотой ω
= π/2 с-1.
Точка совершает колебания по закону
,
где А=
5 см; ω
= 2 с-1.
Определить ускорение
точки
в момент времени, когда ее скорость
см/с.Точка совершает гармонические колебания. Наибольшее смещение
точки равно
10 см, наибольшая скорость
=
20 см/с. Найти
циклическую частоту ω
колебаний и максимальное ускорение
точки.Максимальная скорость точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение =100 см/с2. Найти циклическую частоту ω колебаний, их период Τ и амплитуду А. Написать уравнение колебаний, приняв начальную фазу равной нулю.
Точка совершает колебания по закону
.
В
некоторый момент
времени смещение х1
точки
оказалось равным 5 см. Когда фаза
колебаний увеличилась вдвое, смещение
х2
стало
равным 8 см. Найти
амплитуду А
колебаний.Колебания точки происходят по закону
.
В некоторый момент времени смещение х
точки
равно 5 см, ее скорость
=
20 см/с и ускорение
=
- 80 см/с2.
Найти амплитуду А, циклическую частоту
ω,
период Τ
колебаний
и фазу
в
рассматриваемый момент времени.Складываются два гармонических колебания одного направления с одинаковыми периодами Т1=Т2=1,5 с и амплитудами А1=А2=2 см. Начальные фазы колебаний
и
.
Определить амплитуду А и начальную
фазу
результирующего колебания. Найти его
уравнение и построить с соблюдением
масштаба векторную диаграмму сложения
амплитуд.Смещение светящейся точки на экране осциллографа является результатом сложения двух взаимно перпендикулярных колебаний, которые описываются уравнениями:
1)
и
;
2)
и
;
3)
и
.
Применяя графический метод сложения и соблюдая масштаб, построить траекторию светящейся точки на экране. Принять А=4 см.