Численное решение и экономическая интерпретация прямой задачи

В прямой задаче оптимальный ассортимент планируемой неосновной продукции предполагает получение наибольшей выручки, то есть ищется максимум целевой функции с объемами x_j  0, при которых .

Для компьютерного решения на рабочий лист вводятся (копируются) исходные данные и с адресными ссылками на ячейки организуются вычисления (рис. 23.3):

• целевой функции – должно получиться 2900;

• расхода каждого ресурса 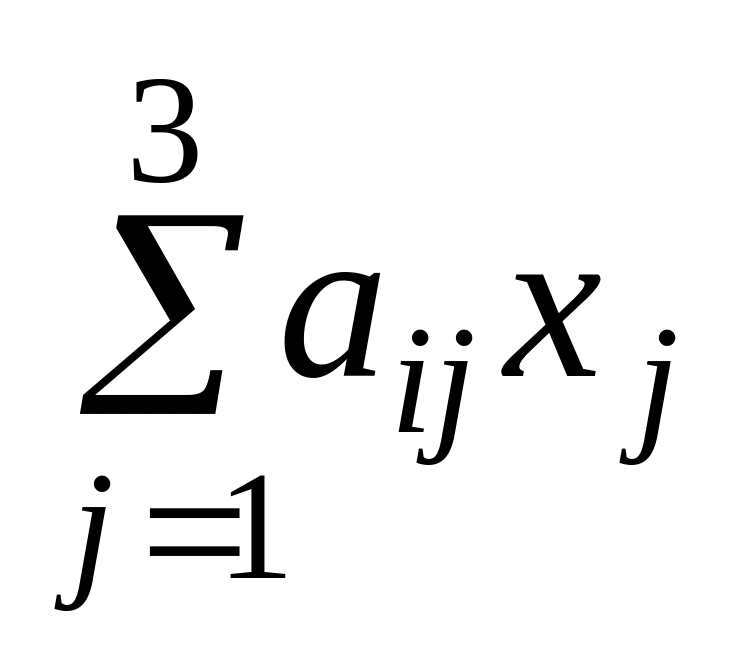– при i = 1, 2, 3 соответственно получится 50, 60 и 120.

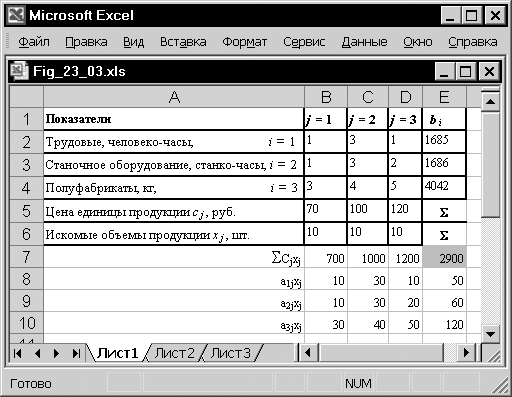
Рис. 23.3. Рабочий лист Excel с алгоритмом решения прямой несимметричной ЗЛП

ЗЛП решаются встроенной в Excel процедурой Поиск решения, вызываемой одноименной командой из меню Сервис. В появляющемся окне диалога вводятся:

• в поле Установить целевую ячейку – адрес целевой функции;

• для флажков Равной:, выбирается Максимальному значению;

• в поле Изменяя ячейки – диапазон клеток с неизвестными x_j;

• кнопкой Добавить вызывается окно диалога Добавить ограничение;

• в окне диалога Добавить ограничение в поле Ссылка на ячейку вводится диапазон с неизвестными x_j, на которые накладывается ограничение по неотрицательности (правее выбирается знак  и еще правее 0);

• кнопкой Добавить опять вызывается диалог Добавить ограничение и вводится ограничение на расход первого ресурса (при i = 1) – указываются ячейка с его суммой, знак = и ячейка с b_i, затем вызов диалога Добавить ограничение повторяется для ввода таких же ограничений на ресурсы при i = 2 и i = 3;

• кнопка ОК возвращает в основной диалог и кнопкой Параметры вызывается диалог с опциями, где достаточно убедиться в установке линейной модели;

• кнопка ОК возвращает в основной диалог, и дается команда Выполнить.

Найденные х₁ = 1075, х₂ = 203 и х₃ = 1 отвечают максимуму целевой функции в сумме 95670.

Экономическим содержанием решения является оптимальный (с максимумом выручки) ассортимент выпуска основной продукции при полном использовании всех имеющихся ресурсов.

Численное решение и экономический смысл двойственной злп

При несимметричной двойственности (как и при симметричной), если одна из связанных задач имеет оптимальное решение, то его имеет и другая, причем экстремальные значения целевых функций равны.

Экономическое содержание этого положения состоит при оптимальном плане производства в совпадении стоимости произведенной продукции и оценки ресурсов, расходуемых на ее выпуск. Оптимальность плана означает точное воплощение в оценке произведенной по этому плану продукции всех имеющихся ресурсов при отсутствии непроизводительных затрат.

Отсюда следует, что минимальная стоимость всех имеющихся ресурсов по теневым ценам (минимум целевой функции в двойственной задаче) также составляет 95670 руб. – равна найденному максимуму целевой функции в прямой задаче (максимальной выручке от реализации продукции из этих ресурсов).

В этом можно убедиться непосредственной оптимизацией теневых цен y_i, решая несимметричную двойственную ЗЛП.

Предварительно на рабочем листе Excel (рис. 23.4) введенные исходные данные дополняются столбцом с первым приближением неизвестных оценок y_i (некоторыми числами, например, по 10). С адресными ссылками организуются вычисления: целевой функции (получится 74130) и оценок ресурсов на единицу продукции каждого типа – при j = 1, 2, 3 должно получиться соответственно 50, 100 и 80.

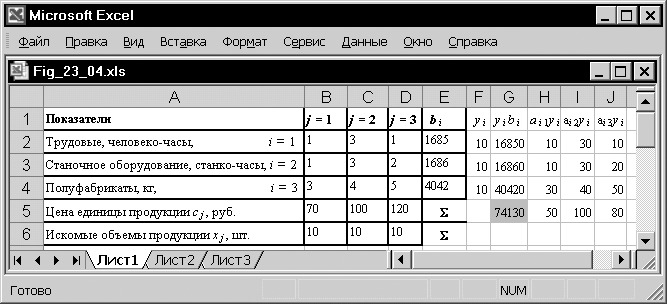
Рис. 23.4. Рабочий лист Excel с алгоритмом решения двойственной несимметричной ЗЛП

Командой Поиск решения из меню Сервис вызывается диалог, где:

• в поле Установить целевую ячейку вводится адрес целевой функции;

• ниже, для флажков Равной:, выбирается Минимальному значению;

• в поле Изменяя ячейки вводится диапазон клеток с оценками y_i;

• кнопкой Добавить выводится окно диалога Добавить ограничение;

• в окне диалога Добавить ограничение в поле Ссылка на ячейку вводится адрес ячейки с суммой оценок ресурсов для единицы продукции первого типа (j = 1), в следующем поле выбирается знак , потом указывается ячейка с с_j;

• кнопкой Добавить повторяется вызов окна диалога Добавить ограничение и ввод таких же ограничений для оценок при j = 2 и затем j = 3;

• кнопка ОК возвращает в окно основного диалога, где кнопкой Параметры вызывается диалог с опциями (достаточно убедиться в установке линейной модели);

• кнопка ОК возвращает в окно основного диалога, и дается команда Выполнить.

В результате находится оптимальное решение (у₁ = -2, у₂ = 6 и у₃ = 22), обеспечивающее минимум целевой функции с ожидавшейся суммой 95670.

Отрицательная оценка у₁ показывает, что имеющиеся трудовые ресурсы избыточны и нерациональны при накладываемом в прямой задаче условии полного использования всех ресурсов. Более гибкое условие – не превышать имеющиеся ресурсы – увеличивает сумму выручки до 97206 при сокращении трудозатрат до 917 человеко-часов вместо планируемых 1685.

Не потому ли трудовые коллективы возражают против денационализации (передачи в частную или акционерную собственность) государственных предприятий? Те стремятся к максимальному доходу, но планируют производство с полным использованием сложившихся объемов всех представляемых ресурсов. Частная собственность побуждает к уменьшению ресурсов и их рациональному использованию, организации вспомогательного производства, сдачи в аренду и т. п. Практически ресурсы, в том числе трудовые, сокращаются, производство интенсифицируется, в предвидении чего и возникает негативная корпоративная реакция, не совпадающая с общенациональными интересами.

Таким образом, найденные в двойственной задаче оценки ресурсов прямо связаны с их вкладом в создаваемую продукцию и доходность, поэтому объемы ресурса с отрицательной оценкой целесообразно уменьшать, а с положительной оценкой – увеличивать.