
- •Энтропия и информация
- •2. Коды источника. Скорость кодирования, скорость создания информации; теоремы Шеннона об источниках; префиксные коды, неравенство Крафта; коды Шеннона – Фено, оптимальные коды Хаффмана.
- •1 Теорема Шеннона(обратная теорема кодирования):
- •2 Теорема Шеннона(прямая теорема кодирования):
- •18. Математическая модель канала связи.
- •19. Линейные коды. Порождающая матрица линейного кода, проверочная матрица. Минимальное кодовое расстояние, теорема Хемминга. Синдромное декодирование. Код Хэмминга, декодирование кодов Хемминга.
- •20. Циклические коды. Порождающий многочлен циклического кода, проверочный многочлен;
Энтропия и информация
виды информации: собственная информация, условная информация, взаимная информация;
энтропия вероятностной схемы и ее свойства;
условная энтропия и ее свойства.
взаимная информация и ее свойства.
дискретный источник без памяти.
а) виды информации: собственная информация, условная информация, взаимная информация; г) взаимная информация и ее свойства;
Определение
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Определение
Конечное множество
U
вместе с заданным на нём распределением
вероятностей
![]() называется дискретным
ансамблем
сообщений и обозначается символом
называется дискретным
ансамблем
сообщений и обозначается символом
![]() .
.
Определение
Пусть на множестве
![]() задано совместное распределение
вероятностей
задано совместное распределение
вероятностей
![]() ,
которое каждой паре
,
которое каждой паре
![]() ,
сопоставляет вероятность
,
сопоставляет вероятность
![]() .
Ясно, что соотношения
.
Ясно, что соотношения
![]() и
и
![]() задают распределение вероятностей
задают распределение вероятностей
![]() и
и
![]() на множествах X
и Y.
Таким образом при задании ансамбля
на множествах X
и Y.
Таким образом при задании ансамбля
![]() фактически задаются ещё два ансамбля
фактически задаются ещё два ансамбля
![]() и
и
![]() .
Ансамбли
и
будем называть совместно задаваемыми
с ансамблем
.
.
Ансамбли
и
будем называть совместно задаваемыми
с ансамблем
.
Определение
Собственная информация - мера неопределенности исхода введеная Шеноном I(xk)=log(1/pk).
Пусть
![]() и
и
![]() совместно заданы с ансамблем
.
Зафиксируем некоторое элементарное
сообщение
совместно заданы с ансамблем
.
Зафиксируем некоторое элементарное
сообщение
![]() и рассмотрим условное распределение
и рассмотрим условное распределение
![]() на X.
Для каждого сообщения
на X.
Для каждого сообщения
![]() в ансамбле
определена собственная
информация:
в ансамбле
определена собственная
информация:![]() ,
которая называется условной
собственной информацией
элемента сообщения
,
которая называется условной
собственной информацией
элемента сообщения
![]() при фиксированном сообщении
при фиксированном сообщении
![]() .
.
Определение
Количеством
информации о сообщении
![]() ,
содержащейся в сообщении
,
содержащейся в сообщении
![]() ,
называется величина
,
называется величина
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Поэтому количество информации о сообщении
и сообщении
равно количеству информации о сообщении
в сообщении
,
то есть
.
Поэтому количество информации о сообщении
и сообщении
равно количеству информации о сообщении
в сообщении
,
то есть
![]() .
.
На этом основании
![]() называют количеством
взаимной информации
между сообщениями x
и y
или просто взаимной
информацией
между сообщениями x
и y.
называют количеством
взаимной информации
между сообщениями x
и y
или просто взаимной
информацией
между сообщениями x
и y.
Взаимная информация между сообщениями обладает следующими свойствами:
Если сообщения x и y независимы, то есть
 ,
то сообщение y
не даёт никакой информации о сообщении
x.
В этом случае
,
то сообщение y
не даёт никакой информации о сообщении
x.
В этом случае
 .
.
Если сообщение y содержит в себе сообщение x, то есть
 ,
тогда
,
тогда
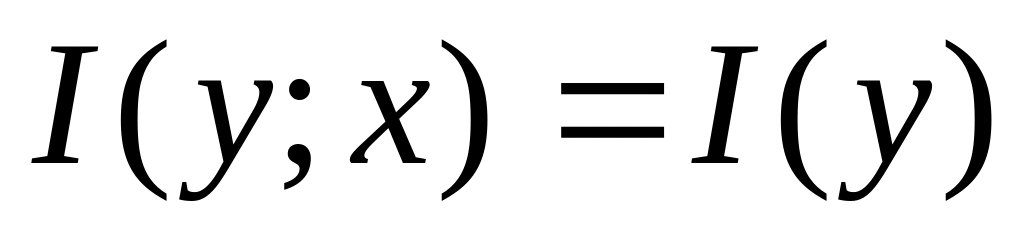
Определение
Математическое ожидание случайной величины на ансамбле называется средним количеством взаимной информации или просто средней взаимной информацией между ансамблями и
![]()
б) энтропия вероятностной схемы и ее свойства;
Определение
Среднее количество информации, содержащееся в отдельном сообщении, называется энтропией источника
![]()
Свойства энтропии
Энтропия любого дискретного источника неотрицательна
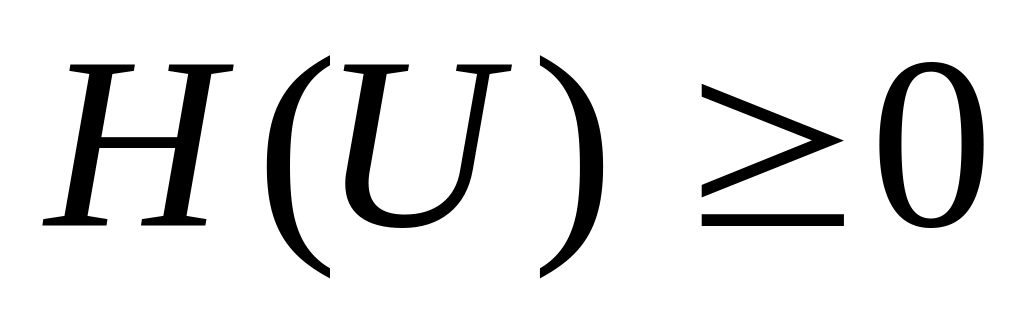 .
Равенство возможно лишь в том случае,
когда источник генерирует одно
единственное сообщение с вероятностью
равной единице.
.
Равенство возможно лишь в том случае,
когда источник генерирует одно
единственное сообщение с вероятностью
равной единице.Пусть N объём алфавита дискретного источника. Тогда
 ,
причём равенство имеет место лишь в
том случае, когда все сообщения
равновероятны.
,
причём равенство имеет место лишь в
том случае, когда все сообщения
равновероятны.

Так как
![]() при
при
![]() и
и
![]() ,
то
,
то

т.е.
![]()
Свойство аддитивности: энтропия нескольких совместно заданных статических дискретных источников сообщений равна сумме энтропий исходных источников.
Энтропия совместного источника , X и Y независимы, равна

в) условная энтропия и ее свойства;
Определение
Математическое
ожидание
![]() случайной величины
случайной величины
![]() ,
определённой на ансамбле
называется условной энтропией ансамбля
X
относительно ансамбля Y.
,
определённой на ансамбле
называется условной энтропией ансамбля
X
относительно ансамбля Y.

Свойства условной энтропии.
1.
![]() ,
равенство имеет место
,
равенство имеет место
![]() когда ансамбли X
и Y
статистически независимы
когда ансамбли X
и Y
статистически независимы
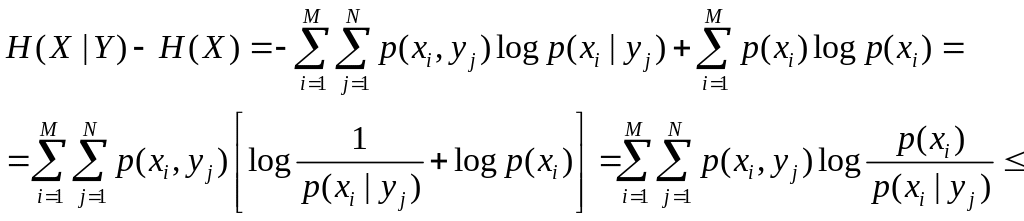

Равенство возможно
когда
![]() ,
то есть когда x
и y
независимы для всех
и
,
то есть когда x
и y
независимы для всех
и
![]()
2. Имеет место соотношение
![]()
называемое свойством
аддитивности энтропии. В самом деле с
помощью равенства
![]() ,
находим
,
находим
![]() .
Аналогично, пользуясь соотношением
.
Аналогично, пользуясь соотношением
![]() можно получить
можно получить
![]() .
.
3.
Свойство аддитивности допускает
обобщение. Если
![]() n
совместно заданных ансамблей, тогда
n
совместно заданных ансамблей, тогда
![]() .
.
Доказательство по индукции:
1)для n =2 доказано выше
2) шаг H(X1...Xn)= H(Xn|X1...Xn-1)= H(X1) + H(X2|X1) + ... + H(Xn|X1....Xn-1) чтд.
Из свойства 3
следует, что
![]() и равенство возможно
когда ансамбли
и равенство возможно
когда ансамбли
![]() статистически независимы, то есть
статистически независимы, то есть
![]() ,
где
,
где
![]() .
Если источники
совпадают с источником
и статистически независимы, то
.
Если источники
совпадают с источником
и статистически независимы, то
![]() .
.
д) дискретный источник без памяти.
Определение
: Дискретным источником без памяти(ДИБП)
называется источник сообщений такой
что для любых
![]() и любой последовательности
и любой последовательности
![]() ,
имеет место равенство
,
имеет место равенство
![]()
