4 Методы первого порядка

Важность прямых методов (методов нулевого порядка), позволяющих получить решение задачи на основании использования только значений целевой функции, несомненна, т.к. в ряде практических инженерных задач информация о значениях целевой функции является единственной надёжной информацией, которой располагает исследователь. С другой стороны, при использовании даже самых эффективных прямых методов для получения решения иногда требуется чрезвычайно большое количество вычислений значений функции. Это обстоятельство наряду с совершенно естественным стремлением к реализации возможности нахождения стационарных точек (т.е. точек, удовлетворяющих условию ) привело к необходимости рассмотрения методов, основанных на использовании градиента целевой функции.

Итак, методы первого порядка служат для решения задач, общая постановка задач которых следующая: дана функция , ограниченная снизу на множестве и имеющая непрерывные частные производные во всех его точках. Требуется найти локальный минимум функции на множестве допустимых решений , т.е. найти такую точку , что

.

4.1 Метод градиентного спуска с постоянным шагом

Стратегия данного метода состоит в построении последовательности точек , таких, что

.

Точку задаёт пользователь. Остальные точки последовательности вычисляются по правилу:

,

где - градиент функции , вычисленный в точке .

Величина шага задается пользователем и остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется путем проверки выполнения условия

или

.

Теорема 1 Пусть функция дифференцируема и ограничена снизу на , а ее градиент удовлетворяет условию Липшица

,

где L>0. Тогда при произвольной начальной точке для метода градиентного спуска с постоянным шагом имеем

.

Эта теорема гарантирует сходимость последовательности к стационарной точке , где . Следовательно, найденную в результате применения метода точку нужно дополнительно исследовать с целью ее классификации.

Оценки скорости сходимости получены только для сильно выпуклых функций, когда последовательность сходится к точке минимума со скоростью геометрической прогрессии:

где - константы.

Алгоритм:

Шаг 1. Задать: начальную точку -малые положительные числа, M – предельное число итераций. Найти градиент в произвольной точке.

Шаг 2. Положить k=0.

Шаг 3. Вычислить .

Шаг 4. Проверить выполнение критерия окончания :

а) если критерий выполняется, , расчет окончен;

б) если нет, то перейти к шагу 5.

Шаг 5. Проверить условие :

а) если неравенство выполняется, то , расчет окончен;

б) если нет, перейти к шагу 6.

Шаг 6. Задать величину шага .

Шаг 7. Вычислить .

Шаг 8. Проверить выполнение условий

(или ):

а) если условие выполнено, то перейти к шагу 9;

б) если нет, то положить и перейти к шагу 7.

Шаг 9. Проверить выполнение условий

:

а) если выполняются оба условия в двух последовательных итерациях с номерами k и k-1, то расчет окончен, найдена точка ;

б) если не выполняется хотя бы одно из условий, то положить k = k + 1 и перейти к шагу 3.

Геометрическая интерпретация метода для n = 2 приведена на рисунке 4.1.

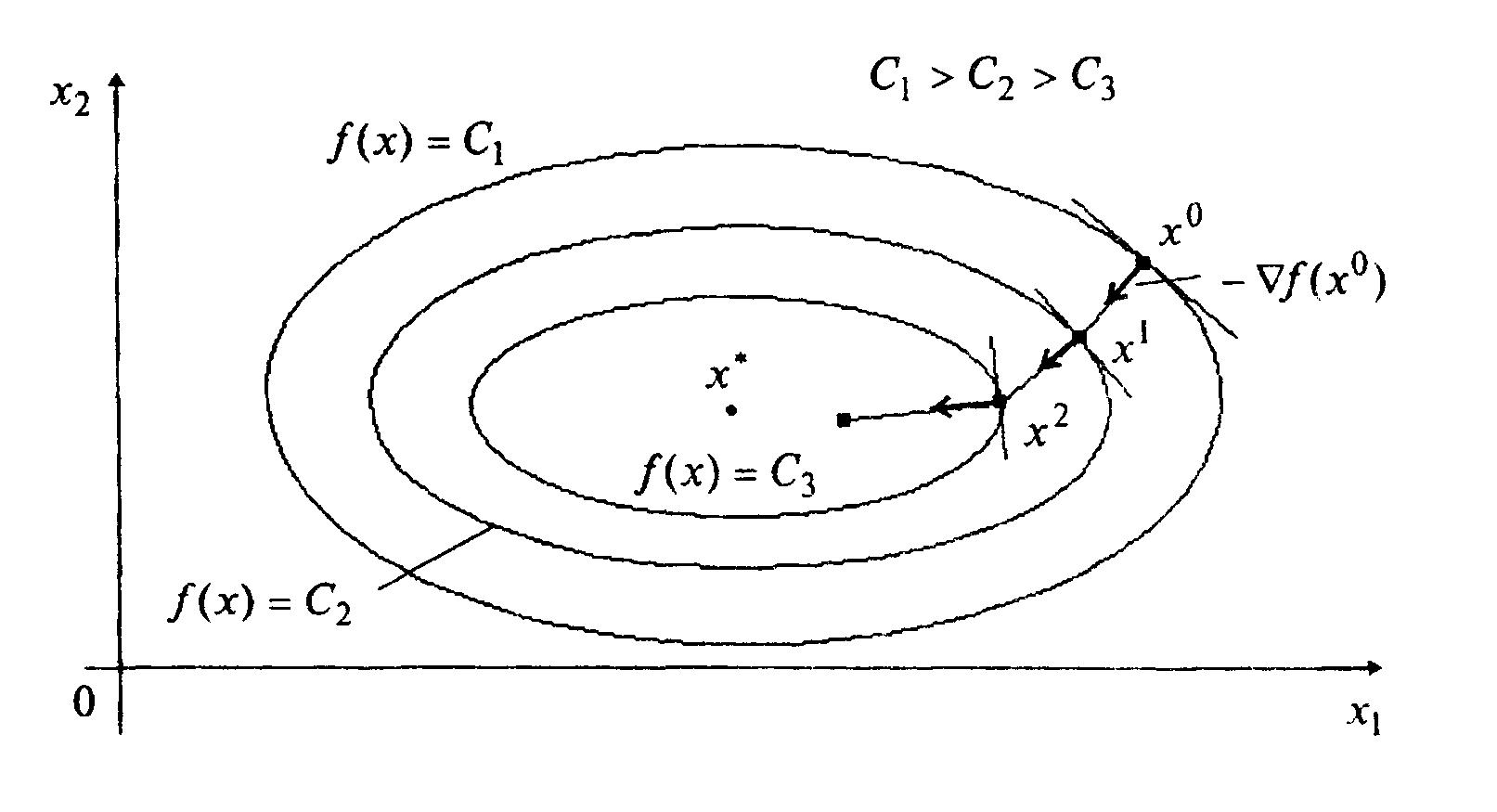
Рисунок 4.1.

Решение поставленной задачи происходит следующим образом: после того, как найдена точка , в которой выполнен по крайней мере один из критериев окончания расчетов, нужно провести анализ точки, чтобы установить, является ли эта точка найденным приближением решения задачи. Процедура анализа определяется наличием у функции непрерывных вторых производных. Если , то следует провести проверку выполнения достаточных условий минимума, т.е.: . Если , то точка есть найденное приближение искомой точки . Если , то следует провести проверку функции на выпуклость в Q – окрестности точки , используя критерий выпуклости для функций : функция выпукла (строго выпукла)в том и только в том случае, если

.

Если функция выпукла (строго выпукла), то есть найденное приближение точки .

Если требуется найти глобальный минимум функции , то для строго выпуклой решение этой задачи аналогично поиску локального минимума функции. Если имеет несколько локальных минимумов, то поиск глобального минимума осуществляется в результате перебора всех локальных минимумов.

Пример: Методом градиентного поиска с постоянным шагом найти локальный минимум функции

Решение:

1. Зададим , M: , , M =10.

Найдем градиент функции в произвольной точке

2. Положим k = 0.

3⁰. Вычислим : .

4⁰. Проверим условие : .

5⁰. Проверим условие : .

6⁰. Зададим .

7⁰. Вычислим : .

8⁰. Сравним с . Имеем . Следовательно, условие для k = 0 не выполняется. Зададим и повторим шаги 7 и 8.

7⁰¹. Вычислим : .

8⁰¹. Сравним с . Вывод: . Переходим к шагу 9.

9⁰. Вычислим и :

.

Вывод: полагаем k = 1 и переходим к шагу 3.

3¹. Вычислим : .

4¹. Проверим условие : .

5¹. Проверим условие : .

6¹. Зададим .

7¹. Вычислим :

.

8¹. Сравним с . Вывод: . Переходим к шагу 9.

9¹. Вычислим и :

.

Вывод: полагаем k = 2 и переходим к шагу 3.

3². Вычислим : .

4². Проверим условие : .

5². Проверим условие : .

6². Зададим .

7². Вычислим :

.

8². Сравним с . Вывод: . Переходим к шагу 9.

9². Вычислим и :

.

Вывод: полагаем k = 3 и переходим к шагу 3.

3³. Вычислим : .

4³. Проверим условие : .

5³. Проверим условие : .

6³. Зададим .

7³. Вычислим :

.

8³. Сравним с . Вывод: . Переходим к шагу 9.

9³. Вычислим и :

.

Условия выполнены при k = 2, 3. Расчет окончен. Найдена точка ; .

Функция является дважды дифференцируемой, поэтому проведем проверку достаточных условий минимума в точке . Для этого проанализируем матрицу Гессе . Матрица постоянна и положительно определена, т.к. оба ее угловых минора и положительны. Следовательно, точка есть найденное приближение точки локального минимума , а значение есть найденное приближение значения . Заметим, что условие , есть одновременно условие строгой выпуклости функции на . Следовательно, , есть найденные приближения точки глобального минимума функции и ее наименьшего значения на .

Геометрическая интерпретация решения задачи представлена на рисунке 4.2.

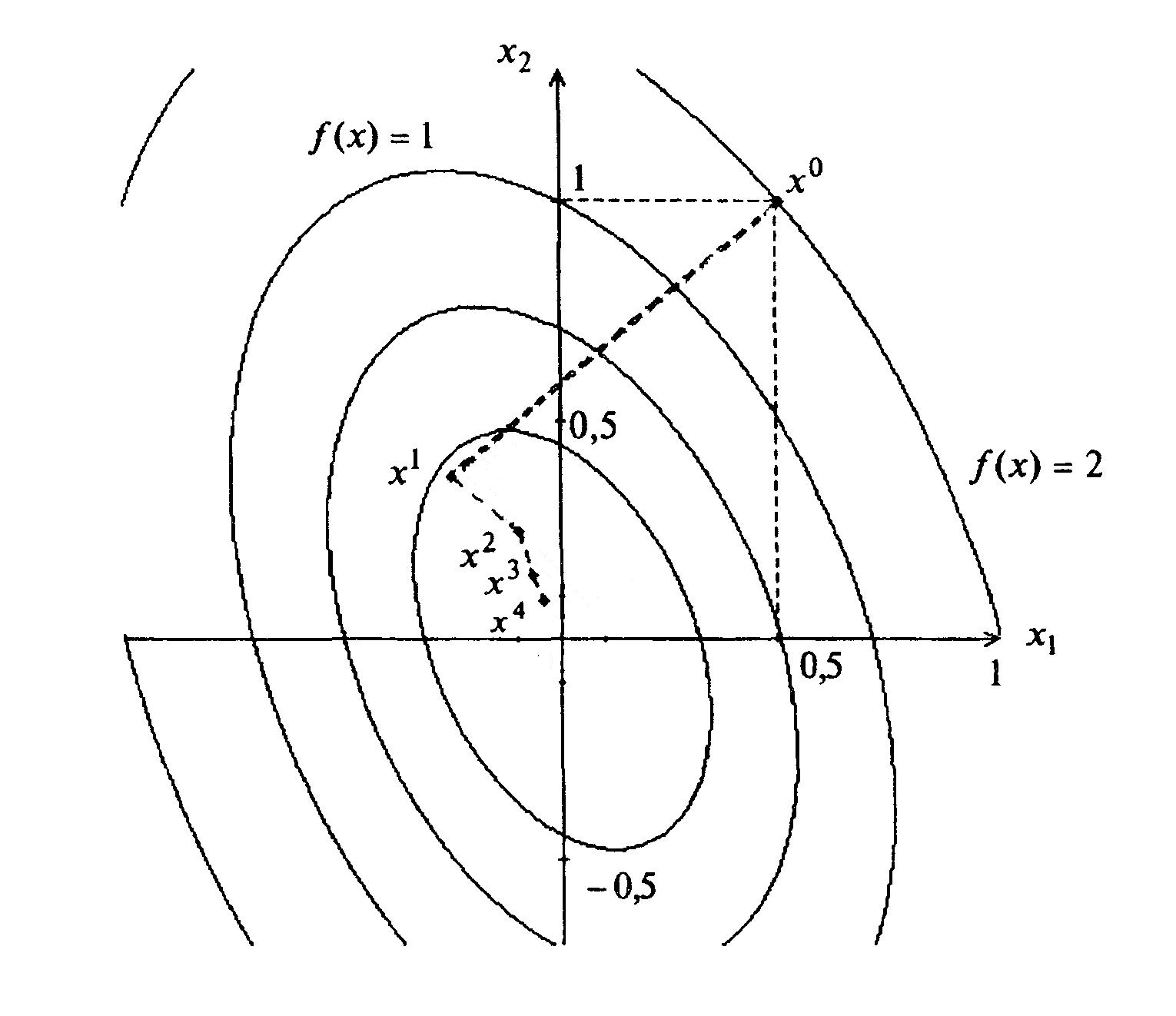
Рисунок 4.2.