3.3 Метод вращающихся координат (метод Розенброка)

Суть метода Розенброка [Rosenbrock H.H.] состоит в следующем. Задается начальная точка. Из нее осуществляется итеративный поиск направления убыва­ния функции с помощью изменяемых дискретных шагов вдоль линейно неза­висимых и ортогональных направлений. В случае удачного шага в исследуемом направлении его значение на следующей итерации увеличивается с помощью коэффициента растяжения, а в случае неудачи уменьшается за счет умножения на коэффициент сжатия (при этом направление поиска изменяется на противо­положное). Поиск в системе текущих направлений проводится до тех пор, пока все возможности уменьшения функции не будут исчерпаны. Если по каждому направлению поиска имеет место неудача, строится новое множество линейно независимых и ортогональных направлений и циклический поиск по отдельным направлениям продолжается. Новые направления поворачиваются по отношению к предыдущим так, что они оказываются вытянутыми вдоль оврага (рис. 3.7).

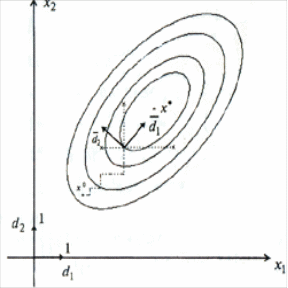
Рисунок 3.7

Алгоритм:

Шаг 1. Задать начальную точку число для остановки алгоритма, коэффициенты растяжения и сжатия , в качестве начальных ли­нейно независимых и ортогональных направлений выбрать коорди­натные направления:

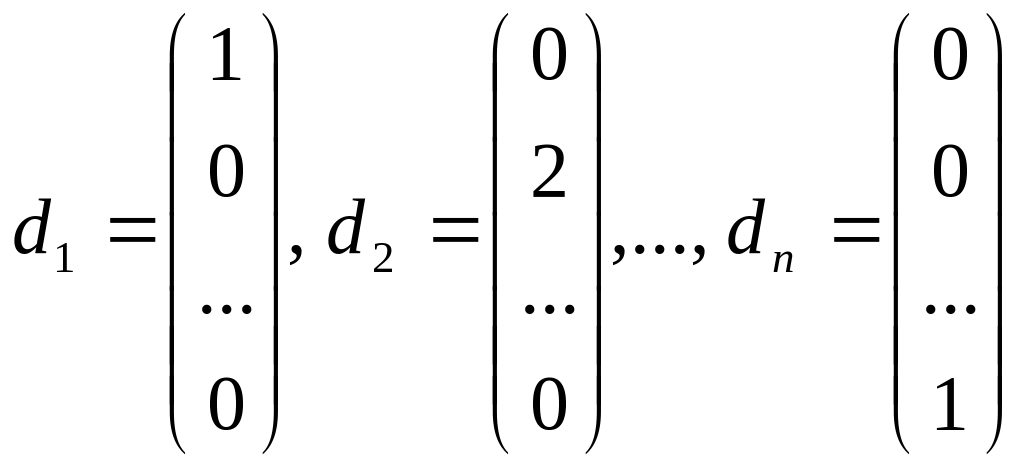
начальную длину шага вдоль каждого из направлений поиска ; - максимальное число неудачных серий шагов по всем направлениям на одной итерации. Положить для всех .

Шаг 2. Сделать шаг по -тому направлению:

1. если , шаг считается удачным. В этом случае следует положить , 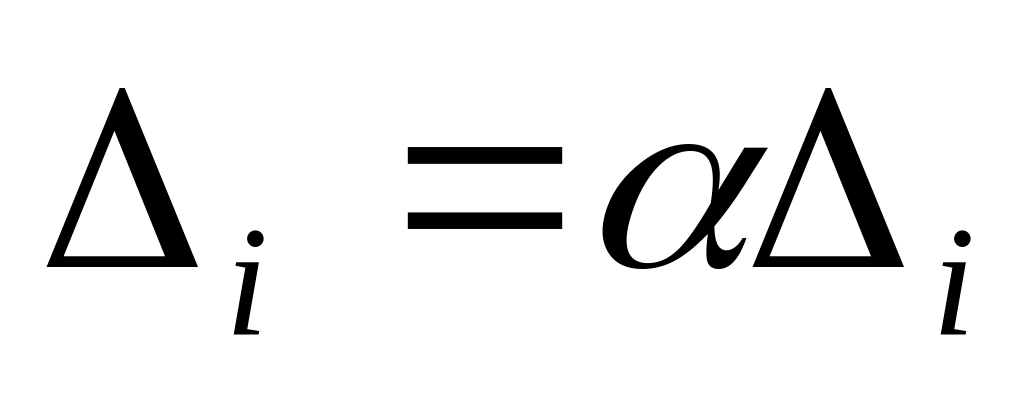и перейти к шагу 3;

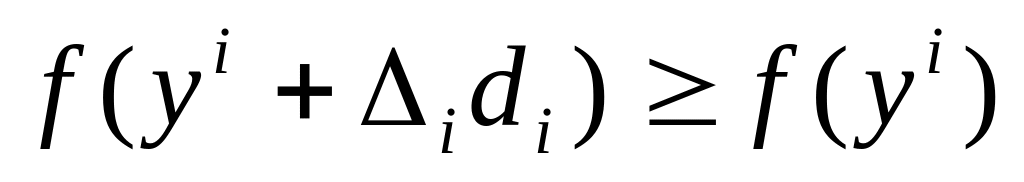2. если , шаг считается удачным. В этом случае следует положить , 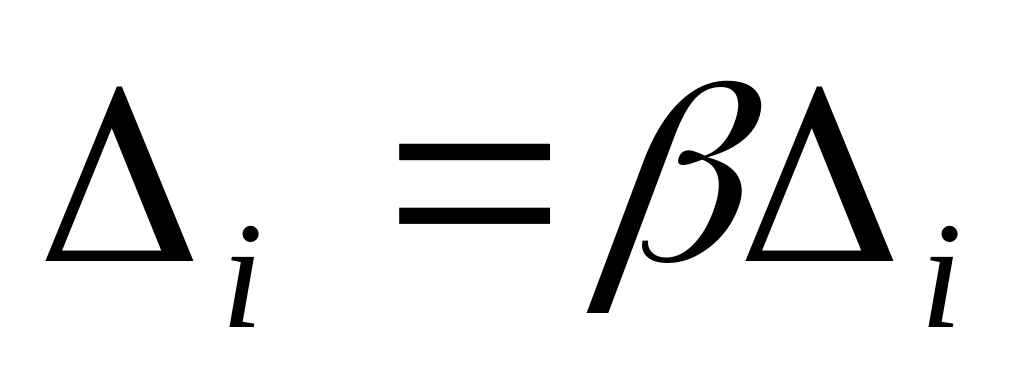и перейти к шагу 3;

Шаг 3. Проверить выполнение условий:

1. если , то положить и перейти к шагу 2 (сделать шаги по оставшимся направлениям);

2. если , проверить успешность поиска по текущим ортогональным направлениям:

• Если 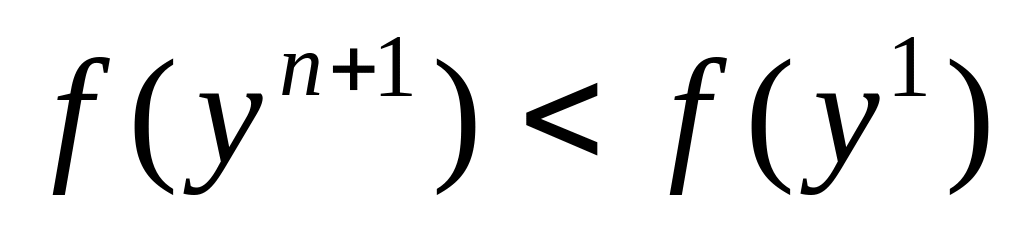, то есть хотя бы один спуск по направлению на шаге 2 был успешным, положить 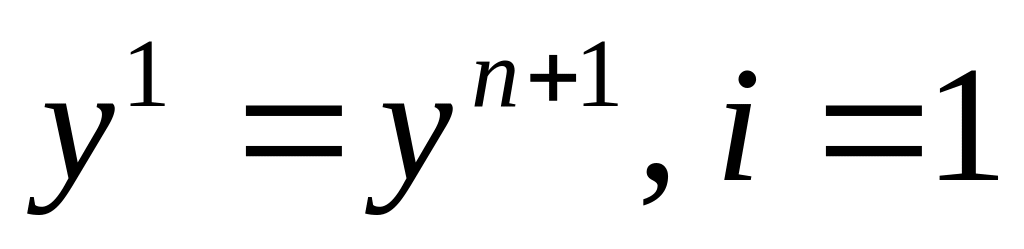и перейти к шагу 2;

• Если 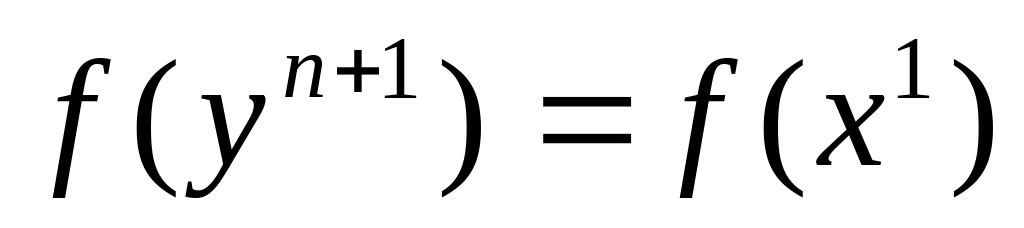, то есть каждый из текущих шагов был неудачным, оценить успешность поиска на текущей итерации:

-- если , то есть на -той итерации хотя бы один шаг удачный, перейти к шагу 4;

-- если , то есть не было ни одного удачного шага на -той итерации, процесс поиска приостановить. Если число последовательно неудач­ных серий шагов по всем направлениям на текущей итерации не превышает , проверить условие окончания, а иначе перейти к шагу 4. Проверяются величины , использованные во время последней серии шагов. Если для всех , то

найдено приближенное решение задачи: . Если хотя бы для од­ного , то положить и перейти к шагу 2.

Шаг 4. Положить и проверить условие окончания

1. если 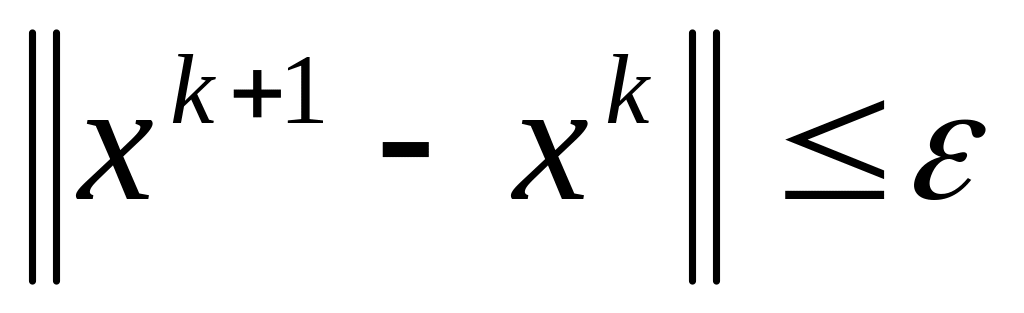, то поиск завершить: ;

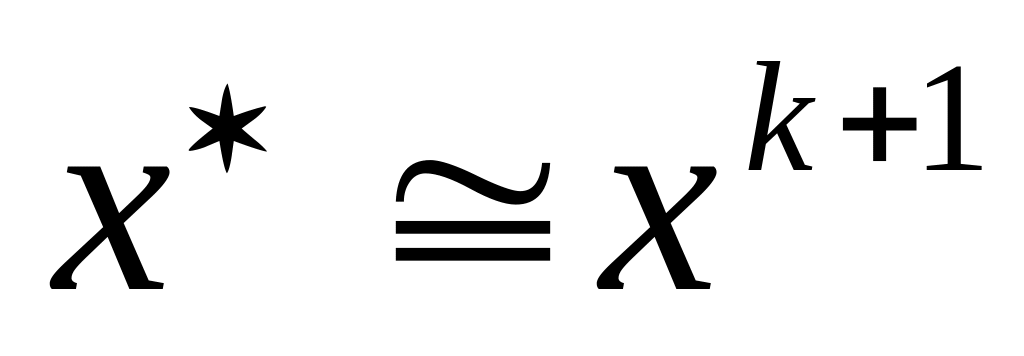2. если 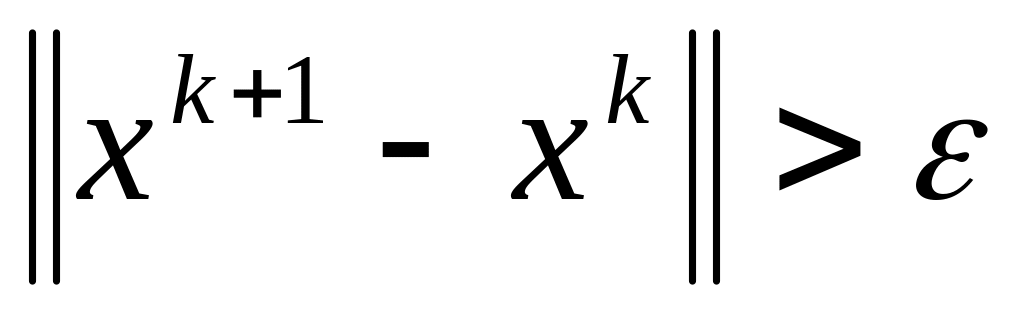, вычислить длины шагов по каждому направлению поиска на -той итерации 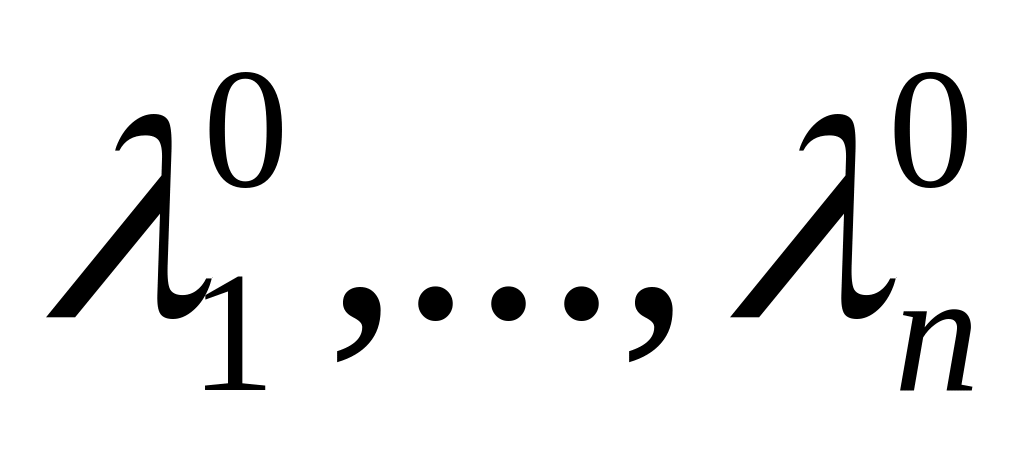из соотношения 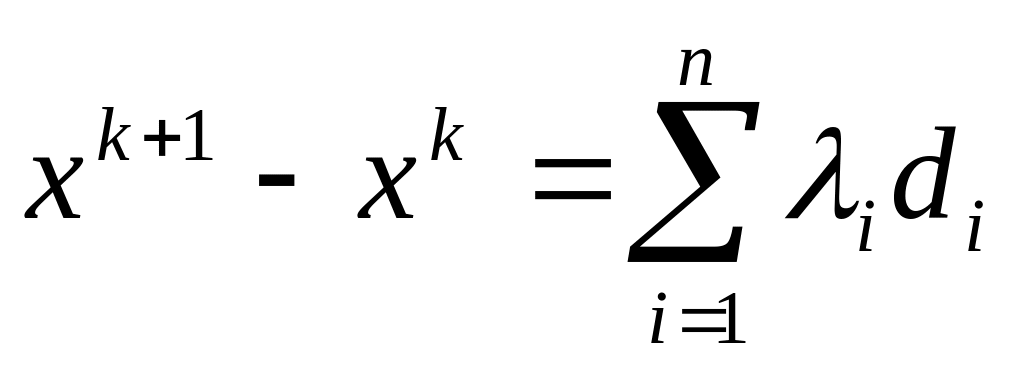. Далее построить новый набор линейно независимых и взаимно ортогональных направлений поиска 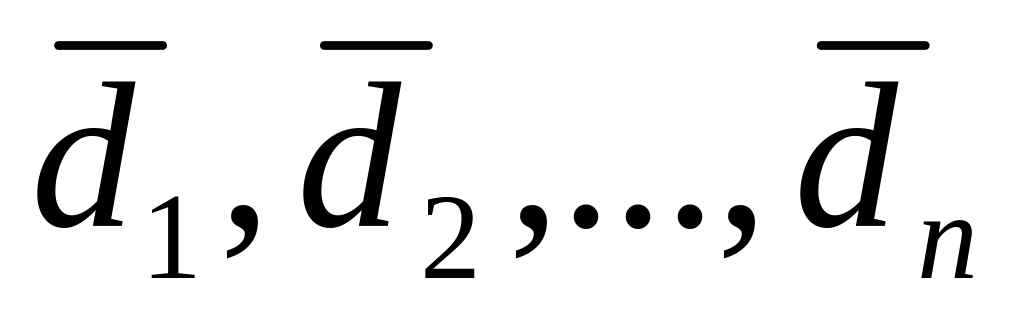с помощью процедуры Грама-Шмидта:

.

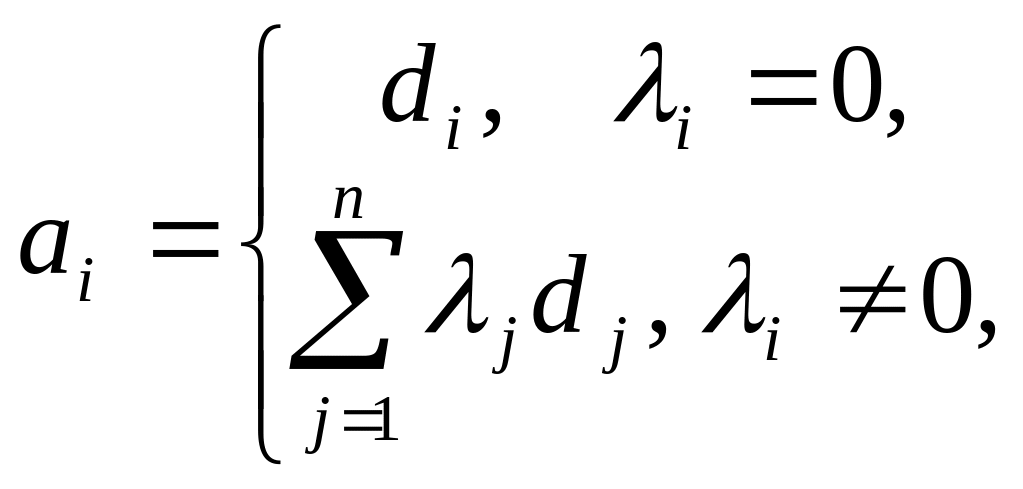
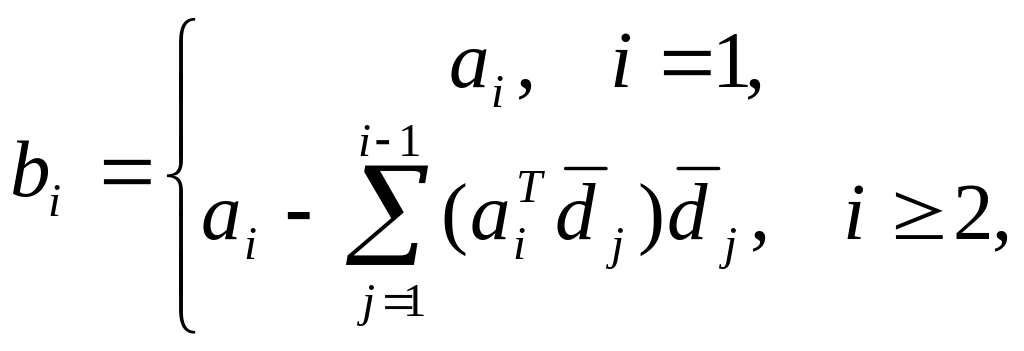
После нахождения новых направлений следует положить: для всех , , и перейти к шагу 2.

Замечание: Розенброк рекомендовал следующие коэффициенты растяжения и сжатия: , .

Пример: Методом вращающихся координат (методом Розенброка) найти локальный минимум функции

Решение:

1. Зададим начальную точку , , , . Пусть .

2⁰. Т.к. , шаг неудачен: .

3⁰. Т.к. i = 1 < 2 = n, то i = i + 1 = 2 и переходим к шагу 2.

2¹. Т.к. то шаг неудачен: .

3¹. Имеем i = 2 = n, , выполнена одна неудачная серия шагов: i = 1 < N = 3. На этой серии поэтому положим и перейдем к шагу 2.

2². Т.к. , шаг удачен: .

3². Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2⁴. Т.к. , шаг удачен: .

3⁴. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2⁵. Т.к. то шаг удачен:

.

3⁵. Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2⁶. Т.к. , шаг удачен: .

3⁶. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2⁷. Т.к. то шаг удачен:

.

3⁷. Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2⁸. Т.к. , шаг неудачен: .

3⁸. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2⁹. Т.к. то шаг неудачен:

.

3⁹. Имеем i = 2 = n, . Т.к. выполняется условие , переходим к шагу 4.

4⁰. Положим .

Т.к. , то вычислим из соотношения . Отсюда .

Построим новый набор направлений поиска:

Положим и перейдем к шагу 2.

2¹⁰.Т.к. , шаг удачен: .

3¹⁰. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2¹¹. Т.к. то шаг удачен:

.

3¹¹. Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2¹². Т.к. , шаг неудачен: .

3¹². Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2¹³. Т.к. то шаг удачен:

.

3¹³. Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2¹⁴. Т.к. , шаг неудачен: .

3¹⁴. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2¹⁵. Т.к. то шаг неудачен:

.

3¹⁵. Имеем i = 2 = n, . Т.к. выполняется условие , переходим к шагу 4.

4¹. Положим .

Т.к. , то вычислим из соотношения . Отсюда .

Построим новый набор направлений поиска:

Положим и перейдем к шагу 2.

2¹⁶. Т.к. , шаг неудачен: .

3¹⁶. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2¹⁷. Т.к. то шаг неудачен:

.

3¹⁷. Имеем i = 2 = n, , выполнена одна неудачная серия шагов: i = 1 < N = 3. На этой серии поэтому положим и перейдем к шагу 2.

2¹⁸.Т.к. , шаг удачен: .

3¹⁸. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2¹⁹. Т.к. то шаг удачен:

.

3¹⁹. Имеем i = 2 = n, . Положим и перейдем к шагу 2.

2²⁰. Т.к. , шаг неудачен: .

3²⁰. Имеем i = 1 < 2 = n, поэтому i = i + 1 = 2 и переходим к шагу 2.

2²¹. Т.к. то шаг неудачен:

.

3²¹. Имеем i = 2 = n, . Т.к. выполняется условие , переходим к шагу 4.

4². Положим .

Т.к. , то процесс поиска завершается: