
- •Киров 2006
- •Рецензент: к.Т.Н., доцент каф. Эвм Матвеева л.И.
- •1 Оформление лабораторной работы
- •1.1 Цель работы
- •1.2 Формирование отчета
- •2 Общие принципы методов поиска безусловного экстремума
- •3 Методы нулевого порядка
- •3.1 Метод конфигураций (метод Хука - Дживса)
- •3.2 Метод деформируемого многогранника
- •3.3 Метод вращающихся координат (метод Розенброка)
- •3.4 Метод сопряженных направлений (метод Пауэлла)
- •4 Методы первого порядка
- •4.1 Метод градиентного спуска с постоянным шагом
- •4.2 Метод наискорейшего градиентного спуска (Метод Коши)
- •4.3 Метод Гаусса - Зейделя
- •4.4 Метод сопряженных градиентов (Флетчера – Ривса)
- •5 Методы второго порядка
- •5.1 Метод Ньютона
- •5.2 Метод Ньютона - Рафсона
- •5.3 Метод Марквардта
- •6 Пример отчета по лабораторной работе
- •7 Блок вариантов заданий
- •8 Библиографический список
3.2 Метод деформируемого многогранника
В
основу метода деформируемого многогранника
(метода Нелдера-Мида [J.A.Nelder, R.Mead]) положено
построение последовательности систем
![]() точек
точек
![]() ,
которые являются вершинами выпуклого
многогранника. Точки системы
,
которые являются вершинами выпуклого
многогранника. Точки системы
![]() на
на
![]() итерации совпадают с точками системы
,
кроме
итерации совпадают с точками системы
,
кроме
![]() ,
где точка
,
где точка
![]() -
наихудшая в системе
,
т.е.
-
наихудшая в системе
,
т.е.
![]() .
Точка
заменяется другой точкой по специальным
правилам, описанным ниже. В результате
многогранники деформируются в
зависимости от структуры линий уровня
целевой функции, вытягиваясь вдоль
длинных наклонных плоскостей, изменяя
направление в изогнутых впадинах и
сжимаясь в окрестности минимума.
Построение последовательности
многогранников заканчивается, когда
значения функции в вершинах текущего
многогранника отличаются от значения
функции в центре тяжести системы
.
Точка
заменяется другой точкой по специальным
правилам, описанным ниже. В результате
многогранники деформируются в
зависимости от структуры линий уровня
целевой функции, вытягиваясь вдоль
длинных наклонных плоскостей, изменяя
направление в изогнутых впадинах и
сжимаясь в окрестности минимума.
Построение последовательности
многогранников заканчивается, когда
значения функции в вершинах текущего
многогранника отличаются от значения
функции в центре тяжести системы
![]() не более чем на
не более чем на
![]() .
.
Алгоритм:
Шаг
1. Задать
координаты вершин многогранника
![]() ;
параметры отражения
;
параметры отражения
![]() ,
сжатия
,
сжатия
![]() ,
растяжения
,
растяжения
![]() ;
число
для остановки алгоритма. Положить
;
число
для остановки алгоритма. Положить
![]() .
.
Шаг
2. Среди
вершин найти “наилучшую”
![]() и “наихудшую”
и “наихудшую”
![]() ,
соответствующие минимальному и
максимальному значениям функции:
,
соответствующие минимальному и
максимальному значениям функции:
![]() ;
;
![]() ,
,
а
также точку
![]() ,
в которой достигается второе по величине
после максимального значение функции
,
в которой достигается второе по величине
после максимального значение функции
![]() .
.
Шаг 3. Найти “центр тяжести” всех вершин многогранника за исключением наихудшей :
![]()
Шаг 4. Проверить условие окончания:
если
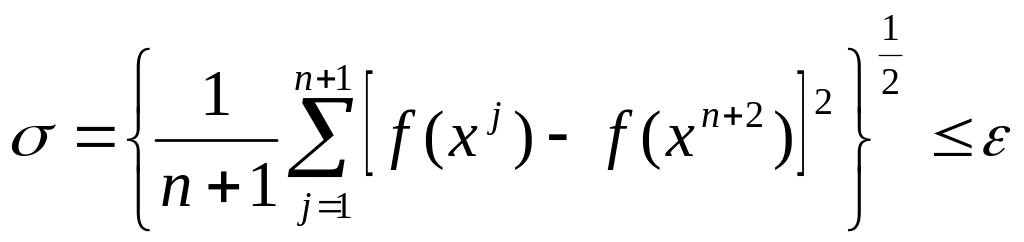 ,
процесс поиска можно завершить и в
качестве приближенного решения взять
наилучшую точку текущего многогранника
,
процесс поиска можно завершить и в
качестве приближенного решения взять
наилучшую точку текущего многогранника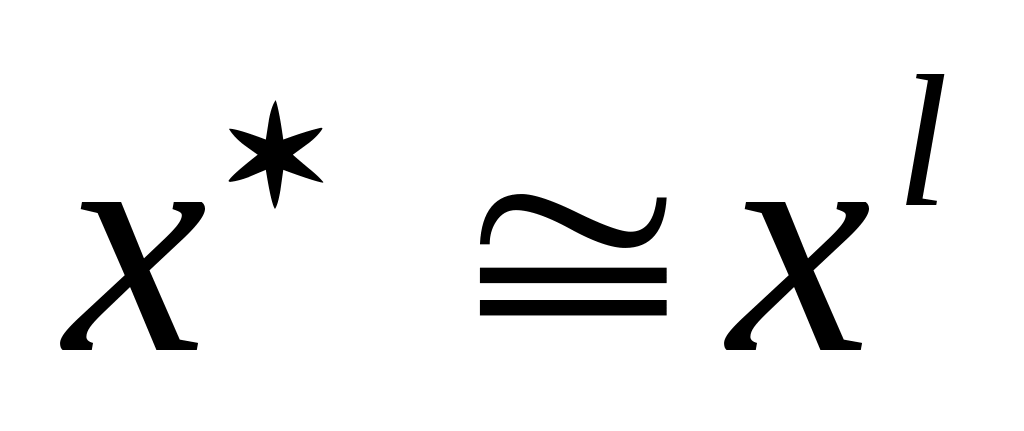 ;
;если
 ,
продолжать процесс.
,
продолжать процесс.
Шаг
5. Выполнить
операцию отражения
наихудшей вершины через центр тяжести
![]() (рисунок 3.3):
(рисунок 3.3):
![]()
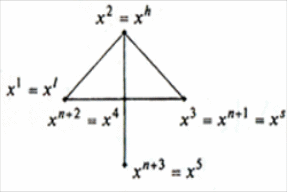
Рисунок 3.3
Шаг 6. Проверить выполнение условий:
если
 ,
выполнить операцию растяжения
(рисунок 3.4):
,
выполнить операцию растяжения
(рисунок 3.4):
![]()

Рисунок 3.4
Найти вершины нового многогранника:
если
 ,
то вершина
заменяется на
,
то вершина
заменяется на
 (при
(при
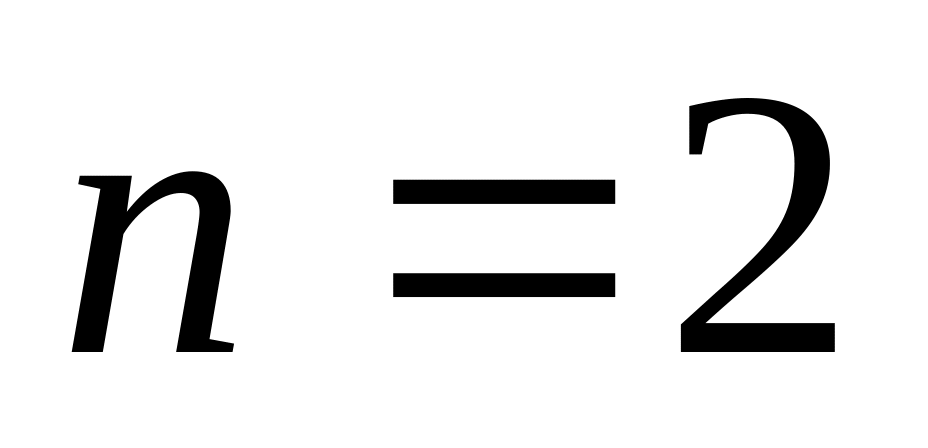 многогранник будет содержать вершины
многогранник будет содержать вершины
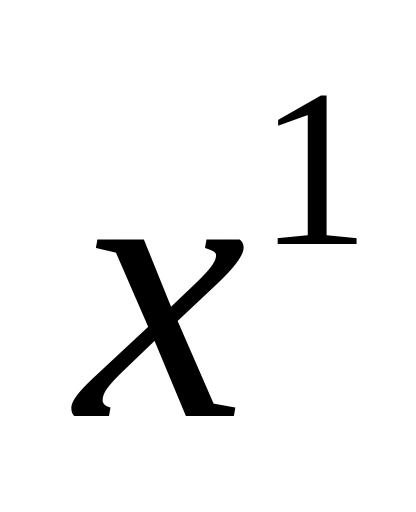 ,
,
 ,
,
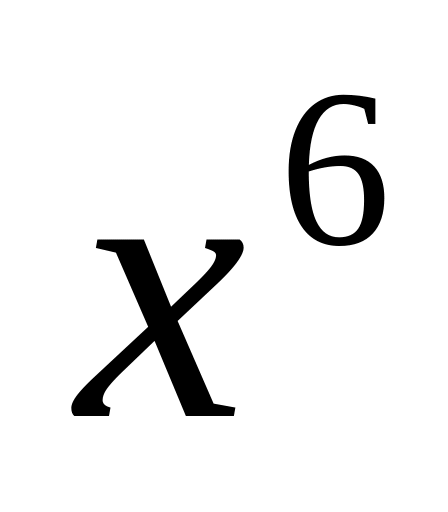 ).
Затем следует положить
и перейти к шагу 2;
).
Затем следует положить
и перейти к шагу 2;если
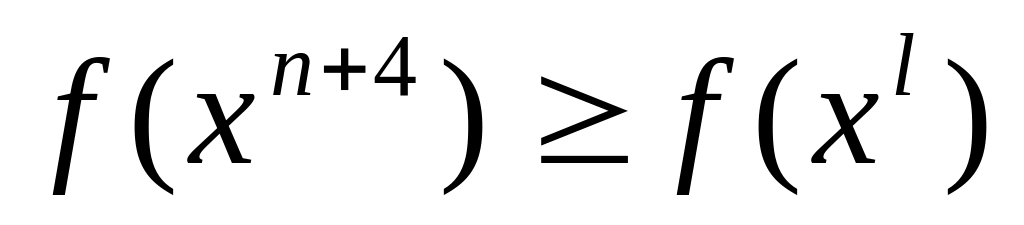 ,
то вершина
заменяется на
,
то вершина
заменяется на
 (при
многогранник будет содержать вершины
,
,
(при
многогранник будет содержать вершины
,
,
 ).
Далее следует положить
и перейти к шагу 2;
).
Далее следует положить
и перейти к шагу 2;
если
 ,
то выполнить операцию сжатия
(рисунок
3.5):
,
то выполнить операцию сжатия
(рисунок
3.5):
![]()

Рисунок 3.5
Следует
заменить вершину
на
![]() ,
положить
и перейти к шагу 2 (при
многогранник будет содержать вершины
,
,
,
положить
и перейти к шагу 2 (при
многогранник будет содержать вершины
,
,
![]() );
);
если
 ,
то вершина
заменить на
.
При этом следует положить
и перейти к шагу 2;
,
то вершина
заменить на
.
При этом следует положить
и перейти к шагу 2;если
 ,
выполнить операцию редукции (рисунок
3.6). Формируется новый многогранник с
уменьшенными вдвое сторонами и вершиной
:
,
выполнить операцию редукции (рисунок
3.6). Формируется новый многогранник с
уменьшенными вдвое сторонами и вершиной
:
![]() .
.

Рисунок 3.6
При этом следует положить и перейти к шагу 2.
Замечание:
Нелдер и Мид
рекомендуют использовать параметры
![]() ,
,
![]() ,
,
![]() ;
Павиани -
;
Павиани -
![]() ,
,
![]() ,
,
![]() ;
Паркинсон и Хатчинсон -
;
Паркинсон и Хатчинсон -
![]() ,
,
![]() ,
,
![]() .
.
Пример: Найти локальный минимум функции методом деформируемого многогранника:
Решение:
1.
Зададим вершины начального многогранника
(треугольник, так как n
= 2 ):
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
20.
Т.к.
![]() то
то
![]() .
.
30.
Найдем центр тяжести вершин
![]() и
:
и
:
![]() .
.
40.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
50. Выполним отражение:
![]()
60.
Т.к.
![]() то вершина
то вершина
![]() заменяется на
заменяется на
![]() .
Положим k
= k
+ 1. Переходим
к шагу 2.
.
Положим k
= k
+ 1. Переходим
к шагу 2.
21.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
то
![]() .
.
31. Найдем центр тяжести вершин и :
![]() .
.
41.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
51. Выполним отражение:
![]()
61.
Т.к.
![]() то выполним сжатие:
то выполним сжатие:
![]() Заменим
вершину
Заменим
вершину
![]() на
.
Положим k
= k
+ 1 = 2 и перейдем
к шагу 2.
на
.
Положим k
= k
+ 1 = 2 и перейдем
к шагу 2.
22.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
.
то
.
32. Найдем центр тяжести вершин и :
![]() .
.
42.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
52. Выполним отражение:
![]()
62.
Т.к.
![]() то выполним редукцию:
то выполним редукцию:
![]()
![]() .
.
Положим k = 3 и перейдем к шагу 2.
23.
Т.к.
![]() то
.
то
.
33. Найдем центр тяжести вершин и :
![]() .
.
43.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
53. Выполним отражение:
![]() .
.
63.
Т.к.
![]() то заменим
на
,
то заменим
на
,
положим k = 4 и перейдем к шагу 2.
24.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
то
![]() .
.
34. Найдем центр тяжести вершин и :
![]() .
.
44.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
54. Выполним отражение:
![]() .
.
64.
Т.к.
![]() то выполним растяжение:
то выполним растяжение:
![]() .
.
Т.к.
![]() то заменим
на
,
положим k
= 5 и перейдем
к шагу 2.
то заменим
на
,
положим k
= 5 и перейдем
к шагу 2.
25.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
то
![]() .
.
35. Найдем центр тяжести вершин и :
![]() .
.
45.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
55. Выполним отражение:
![]() .
.
65.
Т.к.
![]() то заменим
на
,
положим k
= 6 и перейдем
к шагу 2.
то заменим
на
,
положим k
= 6 и перейдем
к шагу 2.
26.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
то
![]() .
.
36. Найдем центр тяжести вершин и :
![]() .
.
46.
Т.к.
![]() ,
процесс продолжается.
,
процесс продолжается.
56. Выполним отражение:
![]() .
.
66.
Т.к.
![]() то выполним редукцию:
то выполним редукцию:
![]()
![]()
![]() .
.
Положим k = 7 и перейдем к шагу 2.
27.
Имеем вершины
![]() .
Т.к.
.
Т.к.
![]() то
.
то
.
37. Найдем центр тяжести вершин и :
![]() .
.
46.
Т.к.
![]() ,
процесс завершается.
,
процесс завершается.
В
качестве приближенного решения выбирается
наилучшая точка
![]() .
.
