
- •Киров 2006
- •Рецензент: к.Т.Н., доцент каф. Эвм Матвеева л.И.
- •1 Оформление лабораторной работы
- •1.1 Цель работы
- •1.2 Формирование отчета
- •2 Общие принципы методов поиска безусловного экстремума
- •3 Методы нулевого порядка
- •3.1 Метод конфигураций (метод Хука - Дживса)
- •3.2 Метод деформируемого многогранника
- •3.3 Метод вращающихся координат (метод Розенброка)
- •3.4 Метод сопряженных направлений (метод Пауэлла)
- •4 Методы первого порядка
- •4.1 Метод градиентного спуска с постоянным шагом
- •4.2 Метод наискорейшего градиентного спуска (Метод Коши)
- •4.3 Метод Гаусса - Зейделя
- •4.4 Метод сопряженных градиентов (Флетчера – Ривса)
- •5 Методы второго порядка
- •5.1 Метод Ньютона
- •5.2 Метод Ньютона - Рафсона
- •5.3 Метод Марквардта
- •6 Пример отчета по лабораторной работе
- •7 Блок вариантов заданий
- •8 Библиографический список
5.3 Метод Марквардта
Стратегия метода Марквардта состоит в построении последовательности точек , таких, что
Точки последовательности вычисляются по правилу
![]()
где
-
задается пользователем, Е – единичная
матрица,
![]() -
последовательность положительных
чисел, таких, что матрица
-
последовательность положительных
чисел, таких, что матрица
![]() положительно
определена. Как правило, число
положительно
определена. Как правило, число
![]() назначается как минимум на порядок
больше, чем самый большой элемент матрицы
назначается как минимум на порядок
больше, чем самый большой элемент матрицы
![]() ,
а в ряде стандартных программ полагается
,
а в ряде стандартных программ полагается
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
В противном случае
.
В противном случае
![]() .
Легко видеть, что алгоритм Марквардта
в зависимости от величины
на каждом шаге по своим свойствам либо
приближается к алгоритму Ньютона, либо
к алгоритму градиентного спуска.
.
Легко видеть, что алгоритм Марквардта
в зависимости от величины
на каждом шаге по своим свойствам либо
приближается к алгоритму Ньютона, либо
к алгоритму градиентного спуска.
Построение последовательности заканчивается, когда либо , либо число итераций , где - малое положительное число, а М – предельное число итераций.
Алгоритм:
Шаг
1. Задать
![]() М
– предельное число итераций. Найти
градиент
и
матрицу Гессе
.
М
– предельное число итераций. Найти
градиент
и
матрицу Гессе
.
Шаг
2. Положить
k
= 0,
![]() .
.
Шаг 3. Вычислить .
Шаг 4. Проверить выполнение условия :
а) если неравенство выполнено, то расчет окончен и ;
б) в противном случае перейти к шагу 5.
Шаг 5. Проверить выполнение условия :
а) если неравенство выполнено, то расчет окончен и ;
б) если нет, перейти к шагу 6.
Шаг 6. Вычислить матрицу .
Шаг
7. Вычислить
матрицу
![]() .
.
Шаг 8. Вычислить .
Шаг
9. Вычислить
![]() .
.
Шаг
10.Вычислить
![]() .
.
Шаг
11. Проверить
выполнение условия
![]() :
:
а) если неравенство выполняется, то перейти к шагу 12;
б) если нет, перейти к шагу 13.
Шаг
12.
Положить
![]() и
перейти к шагу 3.
и
перейти к шагу 3.
Шаг 13. Положить и перейти к шагу 7.
Пример:
Найти локальный минимум функции
Решение:
1. Зададим , M: , , M =10.
Найдем градиент функции в произвольной точке и матрицу Гессе .
2.
Положим k
= 0,
![]() .
.
30. Вычислим : .
40. Проверим условие : .
50. Проверим условие : .
60. Вычислим : .
70.
Вычислим
![]() :
:![]() .
.
80.
Вычислим
![]() :
:![]() .
.
90.
Вычислим
![]() .
.
100.
Вычислим
![]() .
.
110.
Проверим выполнение условия
![]() .
.
120.
Полагаем k
= 1,
![]() и переходим к шагу 3.
и переходим к шагу 3.
31.
Вычислим
:
![]() .
.
41.
Проверим
условие
:
![]() .
.
51. Проверим условие : .
61.
Вычислим
![]() :
:![]() .
.
71.
Вычислим
![]() :
:![]() .
.
81.
Вычислим
![]() :
:![]() .
.
91.
Вычислим
![]() .
.
101.
Вычислим
![]() .
.
111.
Проверим выполнение условия
![]() .
.
121.
Полагаем k
= 2,
![]() и переходим к шагу 3.
и переходим к шагу 3.
32.
Вычислим
:
![]() .
.
42.
Проверим
условие
:
![]() .
.
52. Проверим условие : .
62.
Вычислим
![]() :
:![]() .
.
72.
Вычислим
![]() :
:![]() .
.
82.
Вычислим
![]() :
:![]() .
.
92.
Вычислим
![]() .
.
102.
Вычислим
![]() .
.
112.
Проверим выполнение условия
![]() .
.
122.
Полагаем k
= 3,
![]() и переходим к шагу 3.
и переходим к шагу 3.
33.
Вычислим
:
![]() .
.
43.
Проверим
условие
:
![]() .
.
53. Проверим условие : .
63.
Вычислим
![]() :
:![]() .
.
73.
Вычислим
![]() :
:![]() .
.
83.
Вычислим
![]() :
:![]() .
.
93.
Вычислим
![]() .
.
103.
Вычислим
![]() .
.
113.
Проверим выполнение условия
![]() .
.
123.
Полагаем k
= 4,
![]() и переходим к шагу 3.
и переходим к шагу 3.
34.
Вычислим
![]() :
:
![]() .
.
44.
Проверим
условие
![]() :
:
![]() .
.
54.
Проверим условие
:
![]() .
.
64.
Вычислим
![]() :
:![]() .
.
74.
Вычислим
![]() :
:![]() .
.
84.
Вычислим
![]() :
:![]() .
.
94.
Вычислим
![]() .
.
104.
Вычислим
![]() .
.
114.
Проверим выполнение условия
![]() .
.
124.
Полагаем k
= 5,
![]() и переходим к шагу 3.
и переходим к шагу 3.
35.
Вычислим
![]() :
:
![]() .
.
45.
Проверим
условие
![]() :
:
![]() .
.
55.
Проверим условие
:
![]() .
.
65.
Вычислим
![]() :
:![]() .
.
75.
Вычислим
![]() :
:![]() .
.
85.
Вычислим
![]() :
:![]() .
.
95.
Вычислим
![]() .
.
105.
Вычислим
![]() .
.
115.
Проверим выполнение условия
![]() .
.
125.
Полагаем k
= 6,
![]() и переходим к шагу 3.
и переходим к шагу 3.
36.
Вычислим
![]() :
:
![]() .
.
46.
Проверим
условие
![]() :
:
![]() .
.
Расчет
окончен. Найдена точка
![]() .
.
Проанализируем полученную точку:
Функция является строго выпуклой, т.к. ее матрица вторых производных в силу того, что . Точка является найденным приближением точки минимума .
Решение задачи представлено на рисунке 5.4.
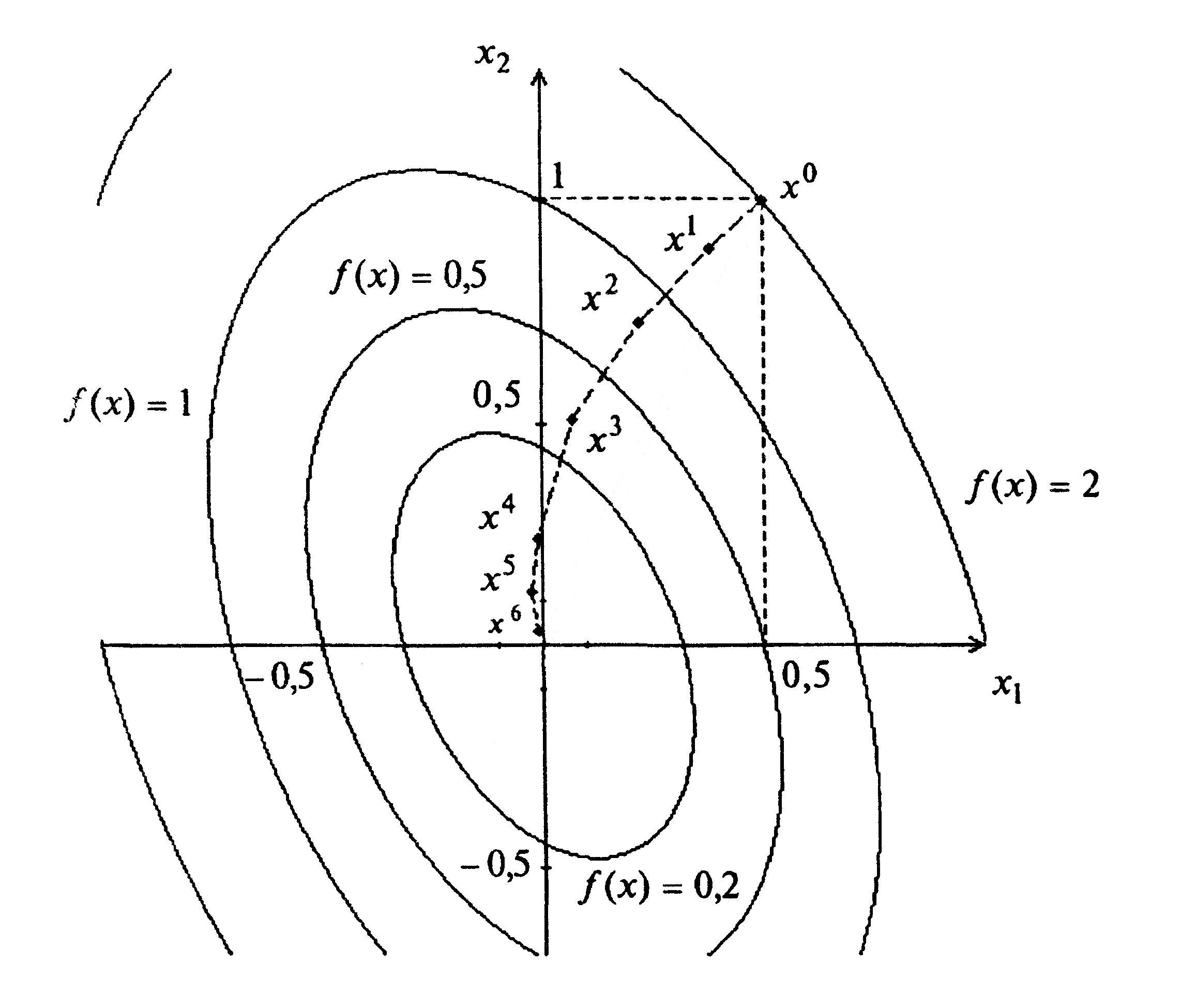
Рисунок 5.4.
