5.3. Приклади задач динамічного прграмування.

У п.5.2 було приведено розв’язок задачі визначення найкоротших відстаней між пунктами відправлення і пунктами призначення, по існуючій транспортній мережі. Така задача «Про найкоротший шлях» є початковим етапом розв’язку таких економічних задач, як оптимальне закріплення споживачів за постачальниками, підвищення ефективності роботи транспорту за рахунок скорочення «пустого» пробігу та інше.

Розглянемо ще декілька прикладів, кожен з яких демонструє метод динамічного програмування.

Оптимальний розподіл інвестицій.

Необхідно розподілити В одиниць наявних грошових засобів серед n підприємств, прибуток g_i(x_i) від яких у залежності від розміру капіталовкладень x_i визначається матрицею (n ;n), яка приведена у таблиці 5.1., так, щоб сумарний прибуток від інвестування був максимальним.

Таблиця 5.1.

x | gi	g1	g2	...	gi	…	gn
x1	g1(x1)	g2(x1)	…	gi(x1)	…	gn(x1)
x2	g1(x2)	g2(x2)	…	gi(x2)	…	gn(x2)
xi	…	…	…	gi(xi)	…	…
xn	g1(xn)	g2(xn)	…	…	…	gn(xn)

Математична модель задачі має вигляд:

визначити Х* = (х₁, х₂, ..., х_і, ..., х_n), які задовольняють умовам:

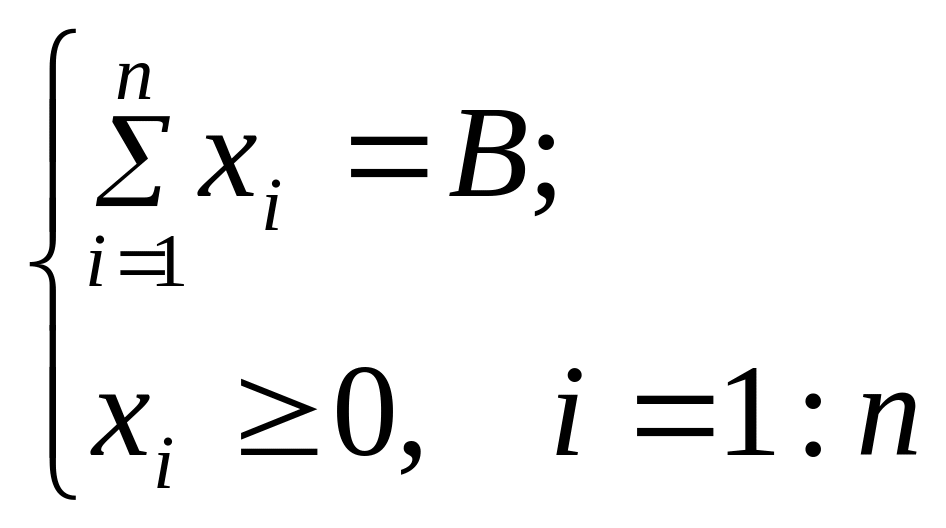(5.4)

і забеспечують максимум цільової функції:

(5.5)

Розіб’ємо процес оптимізації на n кроків і будемо на кожному k –му кроці оптимізувати інвестування не усіх підприємств, а лише підприємств з k–го по n-е. При цьому вважаємо, що у останні підприємства (з першого по (k-1)) також вкладаються кошти, і тому на інвестування з k–го по n-е підприємства залишаються не вся сума, а менша: . Ця величина і буде змінною стану системи.

Змінною управління на k –му кроці буде величина x_k засобів, які вкладаються у k–те підприємство. У якості функції Беллмана F_k(c_k) на k-му кроці можна обрати максимально можливий прибуток, який можна отримати з k–го по n-е підприємства за умови, що на їх інвестування залишилось c_k коштів. Очевидно, що при інвестуванні у k –е підприємство x_k засобів буде отримано прибуток g_k(x_k), а система до (k+1) кроку перейде у стан S_k+1 і відповідно, на інвестування підприємств з (k+1)-го до n-го залишиться c_k+1=( c_k - x_k ) коштів.

Таким чином , на першому кроці умовної оптимізації при k = n функція Беллмана являє собою прибуток лише з n-го підприємства. При цьому на його інвестування може залишитися c_n засобів, . Для отримання максиму прибутку з цього підприємства, можна вкласти в нього усі ці кошти, тобто:

F_n(c_n) = g_n(c_n) і x_n = c_n. (5.6)

На кожному наступному кроці для обчислення функції Беллмана необхідно використовувати результати попереднього кроку. Нехай на k–у кроці для інвестування підприємств з k–го по n-е залишилось c_k засобів. Тоді від інвестування у k–те підприємство x_k засобів, буде отримано прибуток g_k(c_k), а на інвестування підприємств(з k–го по n-е ) залишиться c_k+1=(c_k - x_k ) засобів.

Максимально можливий прибуток, який може бути отриманий від підприємств (з k–го по n-е ), буде рівний:

F_k(c_k) = (5.7)

Максимум виразу (5.7) досягається при деякому значенні x_k^*, яке являється оптимальним управлінням на k–у кроці для стану системи S_k. Діючи таким чином, можна визначити функції Беллмана і оптимальні управління до першого кроку.

Значення функції Беллмана F₁(c₁) представляє собою максимально можливий прибуток з усіх підприємств, а значення x₁^*, на якому досягається максимум, є оптимальною кількісттю коштів, вкладених у перше підприємство. Далі на етапі безумовної оптимізації для усіх наступних кроків обчислюється величина c_k=( c_k-1 - x_k-1) і оптимальним управлінням на k–му кроці є значення x_k , що забеспечує максимум прибутку при відповідному стані системи S_k.

Приклад:5.3. На розвиток трьох підприємств виділено 5 млн.гривень. Відома ефективність капіталовкладень у кожне підприємство, задана значенням нелінійної функції g_i(x_i) представленої у таблиці 5.2.

Необхідно розподілити виділені кошти між підприємствами таким чином, щоб отримати максимальний сумарний прибуток від інвестування. Для спрощення розрахунку вважаємо, що розподіл коштів здійснюється у цілих числах x_i={1, 2, 3, 4, 5} млн.грн.

Таблиця 5.2.

x	g1	g2	g3
0	0	0	0
1	2,2	2	2,8
2	3	3,2	5,4
3	4,1	4,8	6,4
4	5,2	6,2	6,6
5	5,9	6,4	6,9

Розв’язок.

І етап. Умовна оптимізація.

1-й крок: k=3. припустимо, що усі кошти у розмірі 5 млн.грн. віддано третьому підприєству. У цьому випадку максимальний прибуток, як видно з таблиці 5.3., складе g₃(х₃)=6,9 тис.грн., тобто рекурентне співвідношення матиме вигляд:

F₃(с₃) = g₃(х₃).

Таблиця 5.3.

с3| x3	0	1	2	3	4	5	F3(с3)	х3*
0	0	-	-	-	-	-	0	0
1	-	2,8	-	-	-	-	2,8	1
2	-	-	5,4	-	-	-	5,4	2
3	-	-	-	6,4	-	-	6,4	3
4	-	-	-	-	6,6	-	6,6	4
5	-	-	-	-	-	6,9	6,9	5

2-й крок: k = 2. Визначимо оптимальну стратегію розподілу грошових засобів між другим і третім підприємствами. Рекурентне співвідношення Беллмана на цьому кроці:

F₂(с₂) =

Таблиця 5.4.

с2 | x2	0	1	2	3	4	5	F2(с2)	X2*
0	0+0	-	-	-	-	-	0	0
1	0+2,8	2+0	-	-	-	-	2,8	0
2	0+5,4	2+2,8	3,2+0	-	-	-	5,4	0
3	0+6,4	2+5,4	3,2+2,8	4,8+0	-	-	7,4	1
4	0+6,6	2+6,4	3,2+5,4	4,8+2,8	6,2+0	-	8,6	2
5	0+6,9	2+6,6	3,2+6,4	4,8+5,4	6,2+2,8	6,4+0	10,2	3

3-й крок. k=1. Визначаємо оптимальну стратегію розподілу грошових засобів між другим і першим підприємствами, використовуючи наступне рекурентне співвідношення для розрахунку сумарного прибутку:

F₁(с₁) =

на основі якого складено таблицю 5.5.

Таблиця 5.5.

с1 | x1	0	1	2	3	4	5	F1(с1)	х1*
0	0+0	-	-	-	-	-	0	0
1	0+2,8	2,2+0	-	-	-	-	2,8	0
2	0+5,4	2,2+2,8	3+0	-	-	-	5,4	0
3	0+7,4	2,2+5,4	3+2,8	4,1+0	-	-	7,6	1
4	0+8,6	2,2+7,4	3+5,4	4,1+2,8	5,2+0	-	9,6	1
5	0+10,2	2,2+8,6	3+7,4	4,1+5,4	5,2+2,8	5,9+0	10,8	1

ІІ етап. Безумовна оптимізація.

Визначаємо компоненти оптимальної стратегії.

1-й крок. За даними таблиці 5.5 максимальний прибуток при розподілі 5 млн.грн. між трьома підприємствами складає: F₁(с₁=5) = 10,8. млн.грн., при цьому першому підприємству треба виділити х₁^*=1 млн.грн.

2-й крок. Визначаємо розмір гошових засобів, що залишились на долю другого і третього підприємств:

с₂ = с₁- х₁^*=5 – 1 = 4 млн.грн.

За таблицею 5.4 знаходимо оптимальний варіант розподілу 4 млн.грн. між другим і третім підприємствами:

F₂(с₂=4)=8,6 при виділенні другому підприємству х₂^*=2 млн.грн.

3-й крок. Визначаємо величину грошових засобів які лишилися на частку третього підприємства:

с₃ = с₂- х₂^*=4 - 2= 2 млн.грн.

За даними таблиці 5.3. знаходимо:

F₃(с₃=2)=5,4 і х₃^*= 2 млн.грн.

Таким чином, оптимальний план інвестування підприємствмає вигляд: X^* = (1, 2, 2).

Максимальний прибуток від інвестування 5 млн.грн в три підприємства, у відповідності до оптимального плану, складає:

F(5) = g₁(1) + g₂(2)+ g₃(2) = 2,2 + 3,2 +5,4 = 10,8млн.грн

Вибір оптимальної стратегії оновлення обладнання.

Важливою економічною проблемою є своєчасне оновлення існуючого обладнання: автомобілів, станків, телевізорів і т.п. Cтаріння обладнання включає фізичний і моральний знос, у результаті чого зростають витрати на ремонт і обслуговування, знижується ліквідна вартість обладнання.

Задача вибору оптимальної стратегії оновлення обладнання заключається у визначенні оптимальних строків заміни старого обладнання на нове. Критерієм оптимальності є дохід від експлуатації обладнання, або сумарні витрати на експлуатацію на протязі планового періоду.

Припустимо, що планується експлуатація обладнання на протягом деякого періоду часу в n років. Необхідно визначити оптимальний план заміни обладнання з метою отримання максимального доходу за усі n років, враховуючи, що до початку експлуатації вік обладнання складає t₀ років.

Вхідними даними задачі є: річний дохід r(t) від експлуатації обладнання віком t-років, залишкова вартість S(t) існуючого обладнання та ціна нового обладнання P, а також «вік» обладнання t₀ на початок розрахунку.

t	0	1	…	n
r(t)	r(0)	r(1)	…	r(n)
S(t)	S(0)	S(1)		S(n)

При складанні динамічної моделі вибору оптимальної стратегії оновлення обладнання процес заміни розглядається як n -кроковий, тобто період експлуатиції розбивається на n –років.

Виберемо у якості стану оптимізації план заміни обладнання з k–го по n –й роки. Очевидно, що дохід від експлуатації обладнання за ці роки буде залежати від віку обладнання t, на початок стану системи який розглядається, тобто k–го року. На величину t накладаються наступні обмеження: 1≤ t ≤ t₀ + k–1, тобто t не може перевищувати віку обладнання за (k–1)–й рік його експлуатиції з урахуванням віку до початку першого року, який складає t₀ років і не може бути менше одиниці.

Таким чином змінна t у даній задачі є змінною стану системи на k –му кроці.

Змінною управління на k –му кроці є змінна, що може приймати одне з двох значень: зберегти (С) або замінити (Z) обладнання на початку k –го року експлуатації:

X_k(t) =

Функцію Беллмана визначають як максимальний можливий дохід від експлуатції обладнання за роки k–го по n –й, за умови, що на початок k–го року вік обладнання складає t років.

Таким чином рекурентне співвідношення Беллмана на кожному кроці управління має вигляд:

F_k(t) = (5.8)

Функція F_k(t) обчислюється на кожному кроці управління для усіх 1≤ t ≤ t₀ + k–1.

Управління, при якому досягається максимум доходу, являється оптимальним.

Для першого кроку умовної оптимізації при з k = n функція Беллмана представляє собою дохід за останній n-й рік:

F_n(t) = (5.9)

Максимум доходу досягається при деякому управлінні, застосовуючи яке на першому році, визначається вік обладнання на початок другого року. Для даного віку обладнання обирається управління, при якому досягається максимум доходу за роки з другого по n-й і т.д. Як результат, на етапі безумовної оптимізації визначаються роки, на початку яких доцільно виконати заміну обладнання.

Приклад 5.4. Знайти оптимальну стратегію експлуатиції обладнання впродовж 6 років (t), якщо річний прибуток r(t) і залишкова вартість S(t), в залежності від строку експлуатації обладнання, приведені у таблиці 5.6. Вартість нового обладнання Р = 13 ум.одиниць, а вік обладнання на початок експлуатаційного періоду складає 1 рік.

Таблиця 5.6.

t	0	1	2	3	4	5	6
r(t)	8	7	7	6	6	5	5
S(t)	12	10	8	8	7	6	4

Розв’язок.

І етап. Умовна оптимізація

1-й крок. k= 6. для першого кроку можливі стани системи t = 1, 2, 3, 4, 5, 6. функціональне управління має вигляд (5.9):

F₆(1) =

F₆(2) =

F₆(3) =

F₆(4) =

F₆(5) =

F₆(6) =

2-й крок. k = 5. можливі стани системи t = 1, 2, 3, 4, 5. функціональне рівняння має вигляд (5.8):

F₅(t) =

F₅(1) =

F₅(2) =

F₅(3) =

F₅(4) =

F₅(5) =

3-й крок. k = 4. можливі стани системи t = 1, 2, 3, 4 функціональне рівняння має вигляд:

F₄(t) =

F₄(1) =

F₄(2) =

F₄(3) =

F₄(4) =

4-й крок. k = 3. можливі стани системи t = 1, 2, 3 функціональне рівняння має вигляд:

F₃(t) =

F₃(1) =

F₃(2) =

F₃(3) =

5-й крок. k = 2. можливі стани системи t = 1, 2 функціональне рівняння має вигляд:

F₂(t) =

F₂(1) =

F₂(2) =

6-й крок. k = 1. можливі стани системи t = 1 функціональне рівняння має вигляд:

F₁(t) =

F₁(1) =

Результати обчислень функції Беллмана приведені у таблиці 5.7.

Таблиця 5.7.

k / t	1	2	3	4	5	6
1	37
2	21	30
3	26	24	23
4	20	19	17	16
5	14	13	12	11	10
6	7	7	6	6	5	5

У таблиці виділено значення функції, що відповідає стану системи - «заміна обладнання».

ІІ етап. Безумовна оптимізація.

Безумовна опимізація починається з кроку k = 1 (6-й рік). Максимально можливий дохід від експлуатації обладнання за роки з 1-го по 6-й складає F₁(1)= 37 ум.од., без заміни обладнання. Тоді, до початку 2-го року вік обладнання збільшиться на одиницю та складатиме t₂ = t₁ + 1 = 1+1 = 2 роки і обирається оптимальне управління для k = 2, тобто, отримати максимум доходу від експлуатації з 2-го по 6-й роки можливо, якщо обладнання не замінювати на нове.

На початок 3-го року при k =3: t₃ = t₂ + 1 = 2+1 = 3 – для отримання максиму прибутку в наступні роки треба провести заміну обладнання на початку 3-го року.

На початок 4-го року при k =4 вік обладнання буде t₄ =1 рік, так як провели заміну обладнання на попередньому кроці і, для отримання максиму прибутку в наступні роки, не треба виконувати заміну обладнання.

Далі відповідно:

k =5: t₅ = t₄ + 1 = 2 - для отримання максиму прибутку не треба проводити заміну обладнання.

k =6: t₆ = t₅ + 1 = 2+1 = 3 - для отримання максиму прибутку не треба проводити заміну обладнання.

Таким чином за 6 років експлуатації обладнання заміну треба провести один раз – на початку 3-го року експлуатації.

Задача про завантаження. Це задача про раціональне завантаження судна, літака, автомобіля і т.п., що має обмеження на об’єм вантажу або вантажопід’ємність засобу перевезення вантажів. Кожен окремий вантаж, розмішений на засобі перевезення, наприклад на літаку, приносить певний прибуток. Задача полягає у визначенні завантаження літака таким вантажем, що приносить найбільший сумарний прибуток. Така задача відома також під назвою задачі про спорядження, в якій пілот літака повинен визначити найбільш цінні, корисні предмети, які необхідно взяти на борт літака, або як задача про рюкзак, в якій турист повинен визначити перелік корисних предметів для заповнення рукзака.

Рекурентне співвідношення процедури зворотньої прогонки було сформоване для загальної задачі завантаження судна вантажопід’ємністю W предметів (вантажів) п найменувань. Нехай т_і – кількість предметів і-го найменування, що підлягають завантаженню, r_i – прибуток, що приносить перевезення одного завантаженого предмету і-го найменування, w_i – вага одного предмету і-го найменування. Математично ця задача має вигляд цілочисленої задачі лінійного програмування:

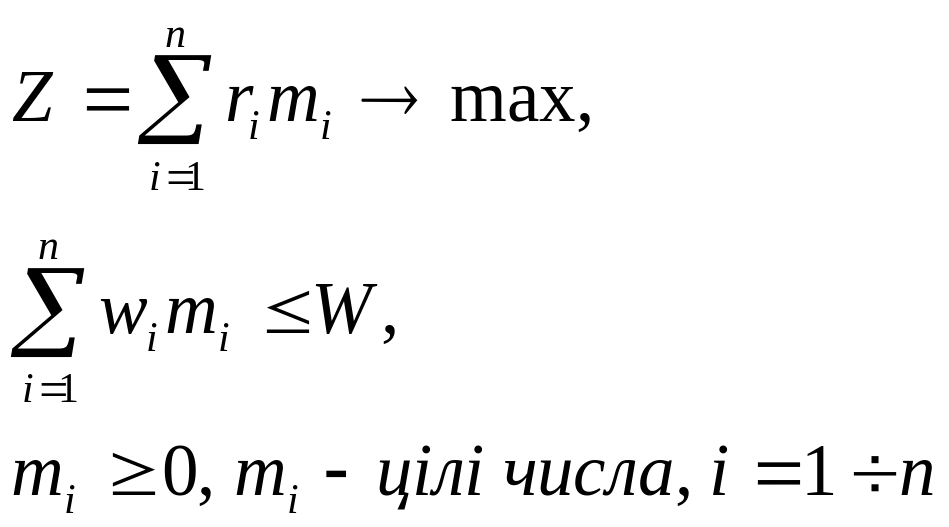(5.10)

Три елемента моделі динамічного програмування визначають наступним чином:

1. Етап (крок) і ставиться у відповідність предмету і-го найменування, і = 1,2, ...,п.

2. Варіанти рішень на етапі і описується кількістю т_і предметів і-го найменування, що підлягають завантаженню. Відповідний прибуток рівний добутку r_i∙ т_і. Значення т_і знаходиться в межах від 0 до 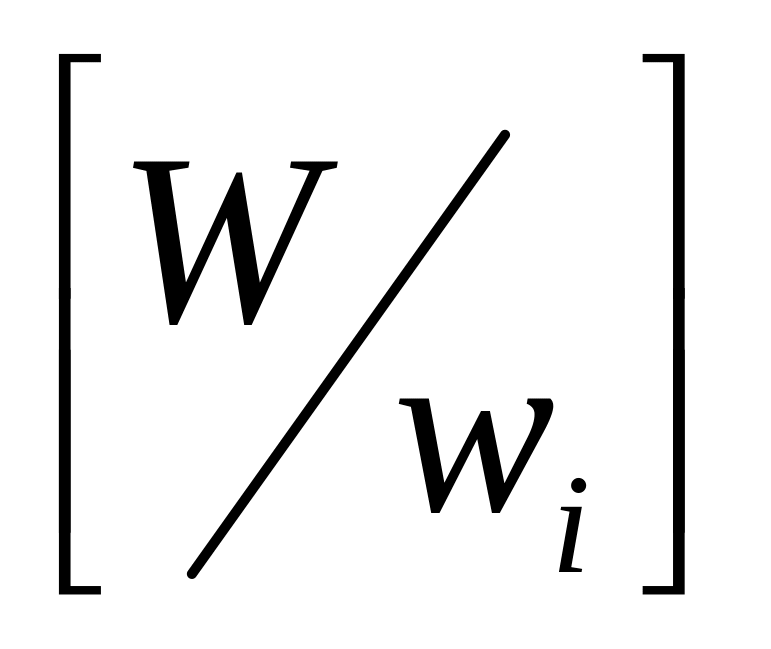, де квадратними дужками позначено цілу частину числа .

3. Стан х_і на етапі і описує сумарну вагу предметів, рішення про завантаження яких прийнято на етапах і, і = 1÷п. Тобто, обмеження на сумарну вагу - єдине, що пов’язує усі п етапів.

Нехай F_i(x_i) – максимальний сумарний прибуток від етапів і, при заданому стані х_і, тоді рекурентне співвідношення можна отримати шляхом наступних міркувань.

Запишемо F_i(x_i) як функцію наступного кроку F_i+1(x_i+1) у вигляді:

(5.11)

Виразимо x_i+1 як функцію x_i . За означенням (x_i - x_i+1) представляє собою вагу завантаженого на етапі і грузу, тому: x_i - x_i+1 = w_i т_і, або x_i+1 = x_i - w_i т_і. Тоді рекурентне рівняння (5.11) приймає наступний вигляд:

(5.12)

Приклад 5.5. Літак, ємністю 4 тони, завантажують предметами 3-х найменувань. Дані про вагу одного предмету w_i в тонах і прибутки r_i∙ в умовних гошових одиницях, від перевезення одиниці вантажу і-го найменування приведені у таблиці:

предмет і	wi	ri∙
1	2	31
2	3	47
3	1	14

Визначити кількість предметів усіх найменувань, завантаження яких принесе найбільший прибуток від їх перевезення.

Розв’язок.

Припустимо, що вага w_i одного предмета для усіх найменувань і приймає лише цілочислові значення, тоді стан оптимізації x_i також буде приймати цілочислові значення. Розв’язок задачі виконаємо за алгоритмом зворотньої прогонки.

І. Умовна оптимізація.

Етап. 3. Точна вага вантажу на 3 етапі наперед невідома, але вона повинна бути в межах від 0 до 4 тон, так як W = 4 тони.

Стани x₃ =0 та x₃ = 4 є крайніми станами системи, так як вони передбачають або повну відсутність предмета 3 на завантаження, або завантаження лише ним усього літака. Решта значень x₃ =1, 2, 3 передбачають часткове завантаження предметом 3 літака. Так як вага предмета 3 рівна 1 тоні, то максимальна кількість одиниць цтого предмету буде: . Цеозначає, що можливі значення стану x₃ будуть 0, 1, 2, 3, 4. Альтернатива т₃ буде допустимою лише за умови, що w₃ т₃ ≤ x₃, тобто усі недопустимі альтернатива виключені.

Основою для порівняння допустимих рішень на етапі 3 буде рівняння Беллмана: ,

У таблиці 5.8. записано порівняння альтернатив для кожного значення x_3.

Таблиця 5.8.

x3	F3(x3) = 14∙ т3					Оптимальне рішення
	т3 = 0	т3 = 1	т3 = 2	т3 = 3	т3 = 4	F3*(x3)	т3*
0	0	-	-	-	-	0	0
1	0	14	-	-	-	14	1
2	0	14	28	-	-	28	2
3	0	14	28	42	-	42	3
4	0	14	28	42	56	56	4

Етап 2.

Таблиця 5.9. Вибір альтернатив для x₂

x2	F2(x2) = 47∙m2 + F3(x2 - 3m2)		Оптимальне рішення
	m2 = 0	m2 = 1	F2*(x2)	m2*
0	0 + 0= 0	-	0	0
1	0 + 14 =14	-	14	0
2	0 + 28 = 28	-	28	0
3	0 + 42 = 42	47 + 0 = 47	47	1
4	0 + 56 = 56	47 + 14 = 61	61	1

Етап 1.

Таблиця 5.10. Вибір альтернатив для x_1.

x1	F1(x1) = 31∙m1 + F2(x1 - 2m1)			Оптимальне рішення
	m1 = 0	m1 = 1	m1 = 2	F1*(x1)	m1*
0	0 + 0= 0	-	-	0	0
1	0 + 14 =14	-	-	14	0
2	0 + 28 = 28	31 + 0 = 31	-	31	1
3	0 + 47 = 47	31 + 14 = 45	-	47	0
4	0 + 61 = 61	31 + 28 = 59	62 + 0 = 62	62	2

ІІ Безумовна оптимізація. Оптимальний розв’язок визначається наступним чином. З умови задачі W = 4 випливає, що перший етап розв’язку задачі при x₁ = 4 дає оптимальне рішення m₁* = 2, яке означає, що два предмета першого найменування будуть завантажені у літак. Тоді для предмету другого найменування змінна стану приймає значення x₂ = x₁ – 2 m₁* = 4 - 2∙2 = 0, тобто оптимальним буде рішення m₂* = 0 - не завантажувати предмет другого найменування в літак. Рішення m₂* = 0 у свою чергу дає значення x₃ = x₂ – 3 m₂* = 0 - 3∙0 = 0, що приводить на третьому етапі до т₃* = 0.

Оптимальним рішення задачі буде такий план завантаження літака в тонах: m₁* = 2; m₂* = 0; m₂* = 0, що забезпечує прибуток 62 умовні грошові одиниці.

Задача планування робочої сили. При виконанні деяких проектів число працюючих, необхідне для виконання робіт деякого проекту, регулюється шляхом їх найму та звільнення. Найм і звільнення робітників пов’язано з додатковими витратами, тому необхідно визначити, яким чином повинна регулюватися чисельність працюючих у період виконання проекту.

Припустимо, що тривалість проекту становить п тижнів і мінімальна кількість робітників, необхідна для виконання робіт на і–му тижні складає b_і чоловік. Ідеальною була б ситуація – протягом і-го тижня чисельність працюючих становить рівно b_і чоловік. Однак, в залежності від вартісних показників, може бути вигідним відхилення чисельності робітників в сторону зменшення або збільшення. Якщо x_і – кількість працюючих на і-му тижні, то можливими є витрати двох видів:

1. C₁(x_i – b_i) – витрати, пов’язані з необхідністю утримання лишньої робочої сили у розмірі (x_i – b_i) одиниць;

2. C₂(x_i – x_i-1) - витрати, пов’язані з необхідністю додаткового найму робочої сили у кількості (x_i – x_i-1) одиниць.

Елементи моделі динамічного програмування визначаються наступним чином:

1. Етап і визначається порядковим номером тижня і (і = 1÷п);

2. Альтернативними рішеннями на і-му етапі будуть значення x_i – кількість працюючих на протязі і-го тижня;

3. Станом на і-му етапі являється x_i-1 - кількість працюючих на протязі (і-1)-го тижня (етапа).

Рекурентне рівняння динамічного програмування записується у вигляді:

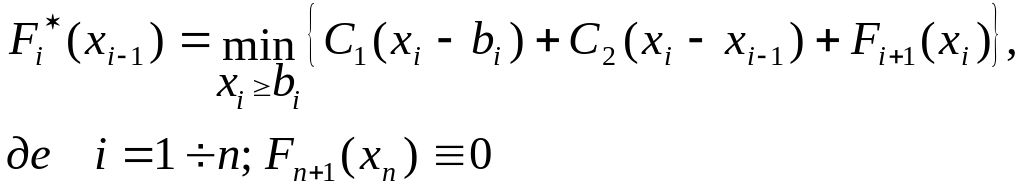(5.13)

Обчислення починаються з етапу п при (x_п = b_п) і закінчуються на етапі 1.

Приклад 5.6. Підрядник будівельної організації оцінює мінімальні потреби в робочій силі на кожен із п’яти тижнів проекту наступним чином: 5, 7, 8, 4, 6 робочих відповідно. Утримання лишку робочої сили обходиться підряднику в 300 гривень за одного робітника в тиждень. Найм робочої сили протягом одного тижня обходиться в 400 гривень плюс 200 гривень за одного працюючого в тиждень. Визначити план найму робочої сили, що забезпечить мінімальні сумарні витрати.

Розв’язок.

Для спрощення розрахунків виразимо С₁ та С₂ в сотнях гривень тоді:

b₁ = 5, b₂ = 7, b₃ = 8, b₄ = 4, b₅ = 6;

C₁(x_i – b_i) = 3(x_i – b_i), x_i > b_i , i=1, 2, 3, 4, 5;

C₂(x_i – x_i-1) = 4 +2(x_i – x_i-1), x_i > x_i-1 , i=1, 2, 3, 4, 5.

І. Умовна оптимізація

Етап 5: b₅ = 6

х4	F5(x4) = C1(x5– 6) + C2(x5 – x4)	Оптимальне рішення
	х5 = 6	F5(x4)	х5*
4	3(0) + 4 + 2(2) = 8	8	6
5	3(0) + 4 + 2(1) = 6	6	6
6	3(0) + 0 = 0	0	6

Етап 4: b₅ = 4

x3	F4(x3) = C1(x4– 4) + C2(x4 – x3) + F5(x4)			Оптимальне рішення
	х4 = 4	х4 = 5	х4 = 6	F4*(x3)	x4*
8	3(0) + 0 + 8 = 8	3(1) + 0 + 6 = 9	3(2) + 0 + 0 = 6	6	6

Етап 3. , b₃ = 8

x2	F3(x2) = C1(x3– 8) + C2(x3 – x2) + F4(x3)	Оптимальне рішення
	x3 = 8	F3*(x2)	x3*
7	3(0) + 4 + 2(1) + 6= 12	12	8
8	3(0) + 0 + 6 = 6	6	8

Етап 2. , b₂ = 7

x1	F2(x1) = C1(x2– 7) + C2(x2 – x1) + F3(x2)		Оптимальне рішення
	x2 = 7	x2 = 8	F2*(x1)	x2*
5	3(0) + 4 + 2(2) + 12 = 12	3(1) + 4 + 2(3) + 6 = 19	19	8
6	3(0) + 4 + 2(1) + 12 = 18	3(1) + 4 + 2(2) + 6 = 17	17	8
7	3(0) + 0 + 12 = 12	3(1) + 4 + 2(1) + 6 = 12	15	7
8	3(0) + 0 + 12 = 12	3(1) + 0 + 6 = 9	9	8

Етап 1. , b₁ = 5

x0	F1(x0) = C1(x2– 5) + C2(x1 – x0) + F2(x1)				Оптимальне рішення
	x1 = 5	x1 = 6	x1 = 7	x1 = 8	F1*(x0)	x1*
0	3(0)+4+2(5)+19=33	3(1)+4+2(6)+17=36	3(2)+4+2(7)+12=36	3(3)+4+2(8)+9=38	33	5

ІІ Безумовна оптимізація. Оптимальне рішення визначається послідовно нпступним чином:

x₀ = 9 → x₁* = 5 → x₂* =8 → x₃ =8 → х₄* = 6→ х₅* = 6.

Отриманому оптимальному рішенню відповідає план найму робітників на протязі п’яти тижнів:

№ тижня (і)	Мінімум робочої сили (bі)	Фактично працюючих (хі)	Рішення
1	5	5	Найняти 5 робочих
2	7	8	Найняти 3 робочих
3	8	8	Нічого не змінювати
4	4	6	Звільнити 2 робочих
5	6	6	Нічого не змінювати

В усіх розглянутих вище задачах динамічного програмування стан системи на будь-якому етапі описувався єдиною змінною. Наприклад, в задачі про завантаженність вага предмету була єдиним обмеженням, що враховувалося при його завантаженні. Разом з тим об’єм предмету також може бути обмежувальною величиною. У такому випадку говорять, що стан системи є двовимірним, так як формується двома змінними: вагою та об’ємом.

Збільшення кількості змінних стану системи приводить до збільшення об’єму обчислень на кожному етапі. Особливо це примітно в моделях динамічного програмування при обчислені яких використовуються таблиці, так як кількість рядків таблиці повинна відповідати кількості комбінацій можливих значень змінної стану. Ці обчислювальні трудощі настільки значні, що в літературі з динамічного програмування отримали назву «прокляття розмірності» [].

Розглянемо приклад для ілюстрації «прокляття розмірності», який до того ж демонструє можливість рішення задачі динамічного програмування методами лінійного програмування.

Приклад 5.7. Деяке виробниче підприємство виготовляє два види продукції. Тривалість виробничого процесу становить 430 хвилин в день. Для виготовлення одиниці продукції першого виду необхідно 2 хвилини, другого виду – 1 хвилина. Денний об’єм виробництва продукції першого виду не обмежений. Максимальний денний попит на продукцію другого виду складає 230 одиниць. Прибуток від реалізації одиниці продукції першого виду – 2 гривні, другого виду – 5 гривень. Визначити оптимальний розв’язок задачі максимізації прибутку методами динамічного програмування.

Дана задача є задачею лінійного програмування, математична модель якої має вигляд:

Z = 2x₁ + 5x₂ → max

Елементи моделі динамічного програмування наступні:

1. Етап і відповідає номеру продукції, і = 1,2.

2. Альтернативою х_і на і-му етапі являється об’єм виробництва продукції і, і = 1,2.

3. Стан (v₁, w₁) описує кількість ресурсів , необхідних для виробництва продукції видів 1 та 2, а саме тривалість виробничого процесу та обмеження на попит , що використовується на етапах 1 та 2.

4. Стан (v₂, w₂) описує кількість ресурсів,необхідних для виробництва продукції видів 1 та 2, а саме тривалість виробничого процесу і обмеження на попит що використовується на етапі 2.

Розв’язок.

Етап 2. Нехай F₂(v₂, w₂) описує максимальний прибуток для етапу 2, тобто прибуток від випуску продукції виду 2, при заданому стані (v₂, w₂). Тоді:

Таким чином, має місце при і рішення другого етапу буде мати наступну форму:

Стан	Оптимальне рішення
	F2(v2, w2)	х2
(v2, w2)

Етап 1:

Оптимізація на етапі 1 потребує розв’язку мінімаксної задачі, що загалом є досить складною справою. Для задачі,що розглядається маємо v₁ =430 та w₁ = 230, що дає інтервал 0 ≤ 2х₁ ≤ 430.

Так як:

min (430 – 2x₁; 230) =

Графічно можна перевірити, що функція F (430, 230) досягає максимального значення при х₁ = 100. Таким чином отримуємо оптимальне рішення етапу 1:

Стан	Оптимальне рішення
	F1(v1, w1)	х1
(430, 230)	1350	100

Для обчислення оптимального значення х₂ розрахуємо обсяги ресурсів, що залишились на частку продукції 2:

v₂ = v₁ -2x₁ = 430 – 200 = 230

w₂ = w₁ - 0= 230.

Тоді = 230

Оптимальне рішення матиме вигляд: Х* = (х₁ = 100; х₂ = 230) одиниць. Zmin = 1350 гривень.