Пример 3.6.2 выполнения задания

Известно, что функция на интервале значений аргумента от –1,6 до 2 имеет несколько точек перегиба, в которых значение хотя бы одной производной больше -1·10³⁰. Требуется найти точку перегиба с максимальным значением производной, изменяя аргумент с шагом 0,001. Вывести найденные приближенные значения производной и соответствующей точки перегиба.

program Project2;

{$APPTYPE CONSOLE}

uses

SysUtils;

const

dX=0.001;

var

Xmax,dYmax,X,dYL,dY,dYR:Extended;

begin

X:=-1.6;

//Приращение функции в точке слева от текущей

dYL:= Sin(5*X)*Sin(X)*Sqr(X)/(X-3)

-Sin(5*(X+dX))*Sin(X+dX)*Sqr(X+dX)/(X+dX-3);

X:=X+dX;

//Приращение функции в текущей точке

dY:= Sin(5*X)*Sin(X)*Sqr(X)/(X-3)

-Sin(5*(X+dX))*Sin(X+dX)*Sqr(X+dX)/(X+dX-3);

Xmax:=X; dYmax:=-1e30;

repeat

X:=X+dX;

//Приращение функции в точке справа от текущей

dYR:= Sin(5*X)*Sin(X)*Sqr(X)/(X-3)

-Sin(5*(X+dX))*Sin(X+dX)*Sqr(X+dX)/(X+dX-3);

if (dY>dYL) and (dY>dYR) or

(dY<dYL) and (dY<dYR) then //Если Х – точка ререгиба

if dY>dYmax then //и dY в ней больше dYmax,

begin //то текущей точкой перегиба

//с максимальной производной станет

Xmax:=X-dX; //текущее значение Х, а текущим

//максимальным приращением в точкой перегиба -

dYmax:=dY; //значение dY.

end;

dYL:=dY;

dY:=dYR;

until X>1.9995;

WriteLn(Xmax,' - точка перегиба, в которой достигается'

,#13#10, dYmax/dX,' - максимум производной');

ReadLn;

end.

Задания 3.6.2 для самостоятельной проработки

Во всех заданиях не использовать аналитических формул производных заданных функций. Вычисленные значения выводить с поясняющими текстами.

1. Составить программу вычисления максимального и минимального значений функции Y=X³-18X²-10X+7 и соответствующие значения аргумента при его изменении на интервале от –4 до 16 с шагом 0,01.

2. Составить программу вычисления значения аргумента, изменяя его на интервале от -1 до 2,5 с шагом 0,001, при котором функция Xsin⁵ (3X) имеет минимальное по абсолютной величине значение производной.

3. Составить программу вычисления максимального значения экстремума-минимума функции X^1/3sin²(10X) и соответствующего значения аргумента при его изменении на интервале от 0,06 до 2,32 с шагом 0,001.

4. Составить программу вычисления минимального расстояния между экстремумами-максимумами функции 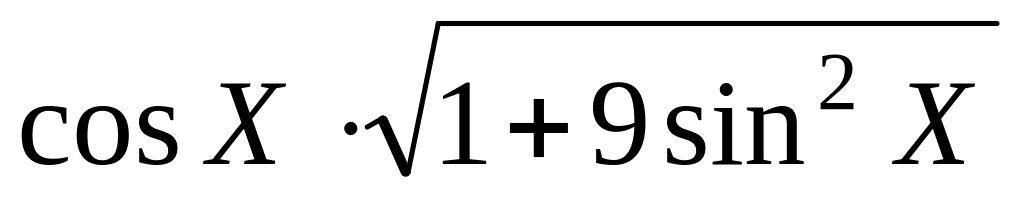и соответствующих значений функции при изменении X на интервале от 8 до 18 с шагом 0,001.

5. Произвольные значения от –3,4 до 1,1 аргумента функции Y=X⁵-18X³-22X² находятся в массиве X(n), n≤20. Составить программу вычисления максимального и минимального значений функции, а также соответствующих значений элементов массива Х и их индексов.

6. Известно, что в интервале от –2 до 8,5 уравнение cos(2,5X)sin²X +0,2=0 имеет несколько корней и что в каждом корне производная функции меньше -1000. Составить программу нахождения корня, в котором производная функции имеет максимальное значение.

7. Известно, что в интервале от –14 до 19 функция 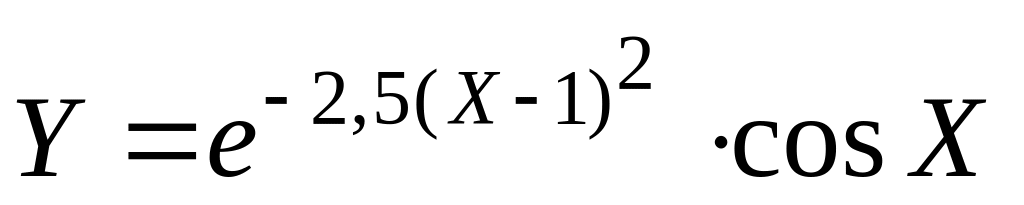имеет несколько точек перегиба со значениями производной в них больше –500. Составить программу нахождения точки перегиба, в которой производная функции имеет максимальное значение.

8. Составить программу вычисления минимального расстояния между соседними корнями уравнения 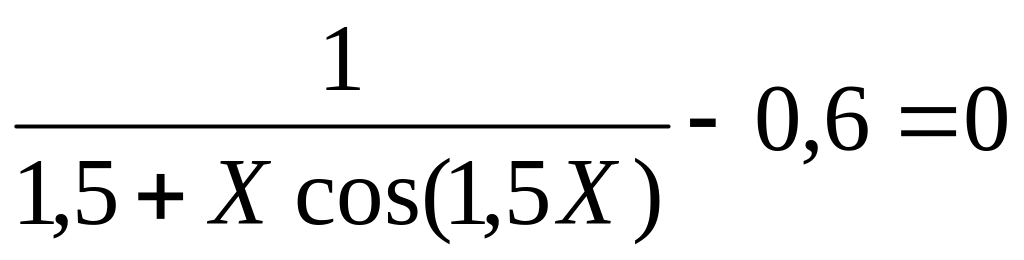, изменяя X на интервале от 1,2 до 16 с шагом 0,0001.

9. Составить программу вычисления значения аргумента, изменяя его на интервале от 6 до 12 с шагом 0,001, при котором производная функции Y=X^0,2·sin² X·cos(3X) имеет минимальное по абсолютной величине значение в точке перегиба.

10. На интервале от -0,5 до 0,3 функция имеет несколько экстремумов. Требуется найти, изменяя аргумент с шагом dX, пару точек экстремума, разность значений функции в которых минимальна.

11. Составить программу вычисления максимального расстояния между экстремумами-минимумами функции 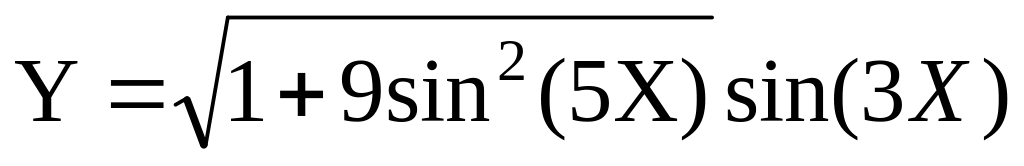и соответствующих значений функции при изменении X на интервале от 2 до 8 с шагом 0,001.

12. На интервале от –1,8 до 1,9 функция Y=cos(5X)·sin²X имеет несколько экстремумов. Требуется найти, изменяя аргумент с шагом dX, точку экстремума-минимума с максимальным значением функции.

13. Составить программу вычисления минимального положительного значения функции Y=10-(2X³+7X²-3X⁴)sin(12X) и соответствующие значения аргумента при его изменении на интервале от –1,5 до 2,2 с шагом 0,001.

14. Найти локальное минимальное приращение расстояния от точки с координатами (Xt,Yt) до кривой Y=X⁵-18X³-22X², изменяя X на интервале от -3 до 0,2 с шагом 0,05.

15. Составить программу вычисления максимального расстояния между корнями уравнения 2cos(2X)+XsinX+0,4=0 с положительным приращением функции в соседних точках, изменяя X на интервале от -2 до 3 с шагом 0,0001.

16. На интервале от 8 до 16 функция Y=cos(5X)sin²X имеет несколько экстремумов. Требуется найти, изменяя аргумент с шагом dX, точку экстремума с максимальным значением функции.

17. В массивах X(N), Y(N), N≤30, заданы координаты точек на плоскости. Найти такое i≤N, для которого расстояние 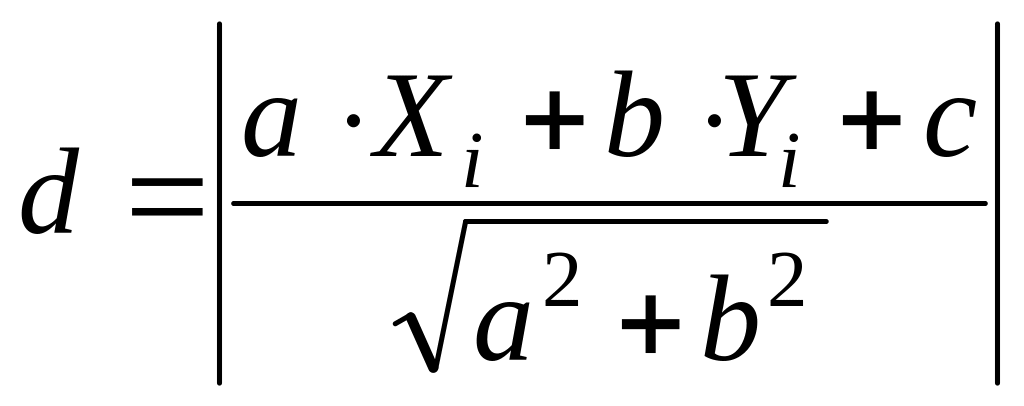от точки (X_i,Y_i) до прямой aX+bY+c=0 минимально.

18. Изменяя аргумент функций Y1=Xsin(5X) и Y2=e^xcos²(2X) на интервале от 0 до 4,15 с шагом 0,0001, найти минимальное расстояние между их экстремумами.

19. Изменяя аргумент функции Y=Xcos(12X)-X*sin(X) на интервале от -1 до 1 с шагом 0,0001, найти минимальное и максимальное её приращения и соответствующие им значения аргумента.

20. Найти минимальное расстояние от точки с координатами (Xt,Yt) до прямых a_iX+b_iY+c_i=0, i=1, 2,…,10, используя формулу расстояния от точки (Xt,Yt) до прямой aX+bY+c=0.

21. ёёёНа интервале от -2 до 6 функция Y=cos(2,5X)sin²X имеет несколько экстремумов. Требуется найти, изменяя аргумент с шагом dX, точку экстремума-максимума с минимальным значением функции.

22. Составить программу вычисления максимального отрицательного значения функции Y= sin ⁵ (3X) +15Xsin⁴(3X)cos(3X) и соответствующие значения аргумента при его изменении на интервале от –4 до 16 с шагом 0,001.

23. Составить программу вычисления минимального расстояния между корнями уравнения 1/(2cosX+Xsin(2X))-0,4=0 с положительным приращением в их окрестностях, изменяя X на интервале от –1,5 до 7 с шагом 0,0001.

24. На интервале от -1 до 8 функция Y=cos(2,5X)sin²X+0,5 имеет несколько экстремумов-минимумов. Требуется найти, изменяя аргумент с шагом dX, минимальный положительный из таких экстремумов и соответствующее значение X.

25. Найти минимальное расстояние от точки с координатами (Xt,Yt) до кривой Y=X²sin(9X), а также соответствующую точку (Xmin,Ymin) на этой кривой.