15

Введение

Цифровая обработка сигналов (ЦОС) – наука, изучающая методы и алгоритмы обработки цифровых сигналов и занимающаяся разработкой аппаратных и программных решений соответствующих систем.

Общие вопросы описания процессов в цифровых системах управления подробно рассмотрены в [3].

Множество задач, решаемых ЦОС, подразделяется на две группы: анализ сигналов и их синтез. Задачей анализа сигналов является выделение небольшой группы значимых параметров, максимально полно описывающих сигнал. Синтез сигналов по совокупности описывающих их параметров – процедура, обратная анализу.

В основе решения этих задач лежат три основных типа преобразований:

• вычисление свертки последовательностей;

• вычисление корреляционных функций;

• дискретное преобразование Фурье.

Цифровой фильтр – это линейная импульсная система, которая осуществляет преобразование входного сигнала в соответствии с заданной амплитудно-частотной (АЧХ) или фазо-частотной характеристикой (ФЧХ).

Данное учебное пособие посвящено рассмотрению вопросов цифровой фильтрации, которые являются основой синтеза цифровых сигналов. Представленный материал структурирован в соответствии с классификацией фильтров на одномерные и многомерные; нерекурсивные и рекурсивные. Большое внимание уделено такой быстро развивающейся и широко применяемой области цифровой фильтрации, как обработка цифровых изображений. Изложенный в конспекте теоретический материал закрепляется в ходе выполнения соответствующих практических и лабораторных работ [14,15].

1. Фильтры с конечной импульсной характеристикой

1.1. Структурная схема фильтров с конечной импульсной характеристикой

Фильтры c конечной импульсной характеристикой (КИХ-фильтры, FIR-фильтры (Finite Impulse Response Filter)) длиной N в общем случае описываются следующим разностным уравнением [6]:

, (1.1)

где – входной сигнал фильтра;

– выходной сигнал фильтра;

– коэффициенты фильтра.

Передаточная функция КИХ-фильтра получается в результате применения к разностному уравнению (2.2.1) –преобразования и равна:

. (1.2)

Структурная схема КИХ-фильтра представлена на рис. 1.1.

Простейшим примером КИХ-фильтра является вычисление скользящего среднего:

. (1.3)

Если на вход такого фильтра подать единичную ступеньку, то выходные значения будут нарастать до установившего значения в течение – периода дискретизации. Если

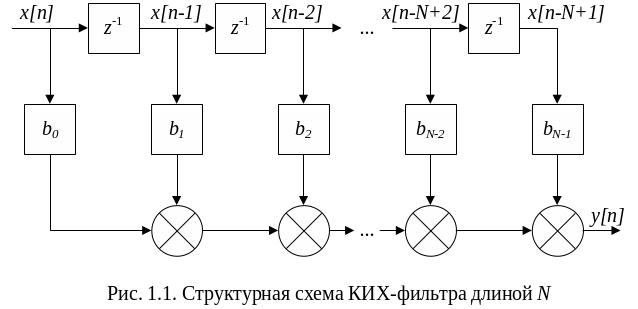
Рис. 1.2. Реакция на единичную ступеньку скользящего среднего

,

то

;

;

;

…

;

.

Импульсная характеристика фильтра представлена на рис. 1.2. Как видно из рисунка величина запаздывания будет расти с ростом порядка фильтра (его длины) и равна периодов дискретизации (рис. 1.3).

Если длина фильтра , то разностное уравнение (1.3) имеет вид:

,

Передаточная функция описывается выражением:

.

Рис. 1.3. Реакция скользящего среднего на одиночный единичный импульс

Рис. 1.4. АЧХ скользящего среднего длины 2.

АЧХ такого фильтра представлена на рис. 1.4:

,

где – период дискретизации.