
Влияние неупругих столкновений
Процессы
возбуждения и ионизации, а также обратные
им процессы тушения и рекомбинации
ведут к скачкообразным изменениям
энергии электрона. При этом для каждого
неупругого процесса, при котором
поглощается или выделяется энергия
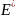 ,
электрон скачком переходит из
энергетического интервала в окрестностях
в интервал
,
электрон скачком переходит из
энергетического интервала в окрестностях
в интервал
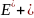 (или наоборот). В этом случае интеграл
столкновения можно символически
представить выражением
(или наоборот). В этом случае интеграл
столкновения можно символически
представить выражением
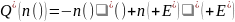 .
(11.37) Первый член справа
описывает уход электронов за счет
неупругого процесса в интервале
.
(11.37) Первый член справа
описывает уход электронов за счет
неупругого процесса в интервале
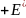 ,
а второй – приход в данный энергетический
интервал электрона, потерявшего энергию
в неупругом столкновении с атомом. Такие
выражения описывают, например, процессы
возбуждения и тущения электронных
термов или колебательных уровней
молекул.
,
а второй – приход в данный энергетический
интервал электрона, потерявшего энергию
в неупругом столкновении с атомом. Такие
выражения описывают, например, процессы
возбуждения и тущения электронных
термов или колебательных уровней
молекул.
В случае ионизации и рекомбинации спектр (в определенных пределах) непрерывен. Поэтому слагаемое, связанное с ионизацией, выглядит несколько сложнее (рождаются два электрона):
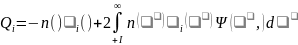 .
(11.38) Здесь
.
(11.38) Здесь
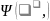 - вероятность того, что один из двух
электронов будет иметь энергию
- вероятность того, что один из двух
электронов будет иметь энергию
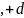 ,
если
,
если
 - энергия налетающего электрона.
- энергия налетающего электрона.
Стационарные фрэ в атомарном газе
Выведенные
уравнения (11.9) и (11.10) для ФРЭ не допускают
общего решения. Поэтому, прежде всего,
будем считать плазму стационарной
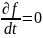 и найдем ФРЭ для случая стационарного
газового разряда в разряженном,
слабоионизованном, атомарном газе.
Температуру газа будем считать достаточно
низкой, чтобы неупругие процессы
оказывали малое влияние на формирование
ФРЭ, тогда членом
и найдем ФРЭ для случая стационарного
газового разряда в разряженном,
слабоионизованном, атомарном газе.
Температуру газа будем считать достаточно
низкой, чтобы неупругие процессы
оказывали малое влияние на формирование
ФРЭ, тогда членом
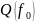 в уравнении (11.36) можно пренебречь.
Проинтегрируем это выражение. Очевидно,
что поток в квадратных скобках в этом
случае равен константе, которая равна
нулю вследствие требования равенства
потока нулю при
в уравнении (11.36) можно пренебречь.
Проинтегрируем это выражение. Очевидно,
что поток в квадратных скобках в этом
случае равен константе, которая равна
нулю вследствие требования равенства
потока нулю при
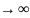 .
Отсюда получаем дифференциальное
уравнение для
.
Отсюда получаем дифференциальное
уравнение для
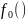 ,
которое легко интегрируется:
,
которое легко интегрируется:
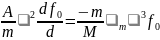 ;
(11.39)
;
(11.39)
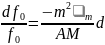 ;
(11.40)
;
(11.40)
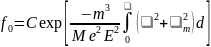 .
(11.41)
.
(11.41)
Дальнейшее
решение возможно только после конкретизации
зависимости
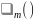 .
Если считать, что частота не зависит от
.
Если считать, что частота не зависит от
 ,
то в результате интегрирования получаем
максвелловскую ФР:
,
то в результате интегрирования получаем
максвелловскую ФР:
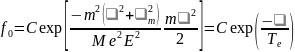 ,
(11.42) где использовано выражение
для средней энергии электронов
,
(11.42) где использовано выражение
для средней энергии электронов
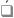 в виде
в виде
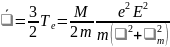 .
(11.43)
.
(11.43)
Часто,
однако, встречается другой случай, когда
транспортное сечение приблизительно
постоянно. В этом случае
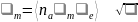 и постоянной можно приближенно считать
длину свободного пробега
и постоянной можно приближенно считать
длину свободного пробега
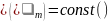 .
Интегрирование тогда дает
.
Интегрирование тогда дает
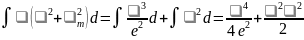 ;
(11.44)
;
(11.44)
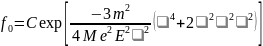 .
(11.45) Такую функцию
называют распределением Маргенау,
которое в постоянном поле
.
(11.45) Такую функцию
называют распределением Маргенау,
которое в постоянном поле
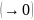 переходит в распределение Дрюйвестейна:
переходит в распределение Дрюйвестейна:
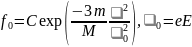 .
(11.45)
.
(11.45)
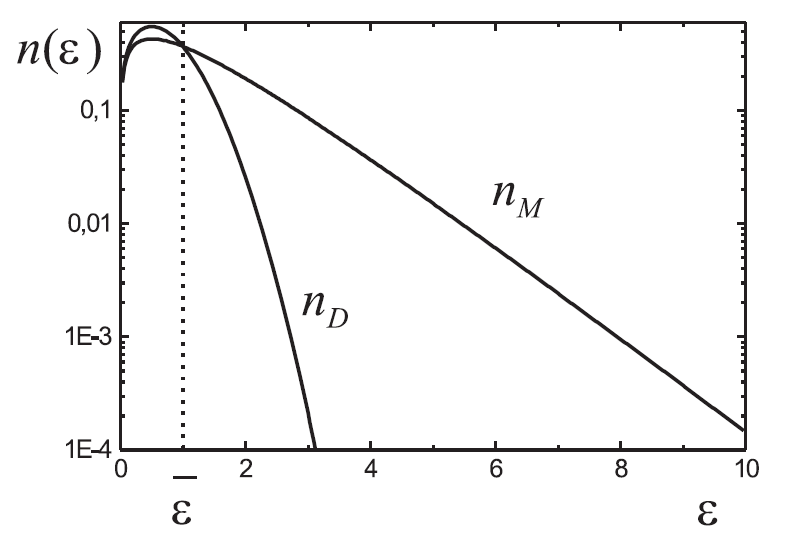
Стационарные функции распределения по энергиям Максвелла и Дрюйвестейна при одинаковой средней энергии (в относительных единицах)
Функция распределения Дрюйвестейна гораздо быстрее спадает в области больших энергий. Это значит, что при равной средней энергии процессы с большим порогом протекают быстрее при максвелловской ФР, чем при дрюйвестейновской.
В общем случае является сложной функцией от скорости, поэтому решение уравнения нужно искать численно, используя экспериментально найденную зависимость . В научной литературе можно найти много примеров подобных расчетов.
