5.1.2. Розгалужені алгоритми (5.2)
У тих випадках, коли перетворення інформації може здійснюватись за різними схемами, залежно від властивостей вхідних даних або проміжних результатів, використовуються розгалужені алгоритми. Тобто в алгоритмі передбачаються всі можливі варіанти обробки інформації, кожний з яких розробляється як окрема гілка алгоритму, а вибір однієї з них для виконання здійснюється за допомогою перевірки деякої умови, що відображає властивості інформації, використовуваної у процесі перетворення. В алгоритмічних системах для цього є розпізнавачі. Залежно від того, на скільки гілок розгалужується алгоритм, він може бути простим або складним. Для простого розгалуженого процесу перевіряється одна умова (один розпізнавач), для складного — дві чи більше умов, кожна з яких відокремлює одну гілку.
Просте розгалуження відбувається за схемою 5.2. Умова формулюється таким чином, щоб відповідь перевірки була «так» чи «ні» (рис. 5.4).
Рис. 5.4. Схема простого розгалуженого процесу 5.2
Приклад 2а. Дано дійсні числа х та у. Обчислити max(x, y). Алгоритм розв’язання на рис. 5.5:
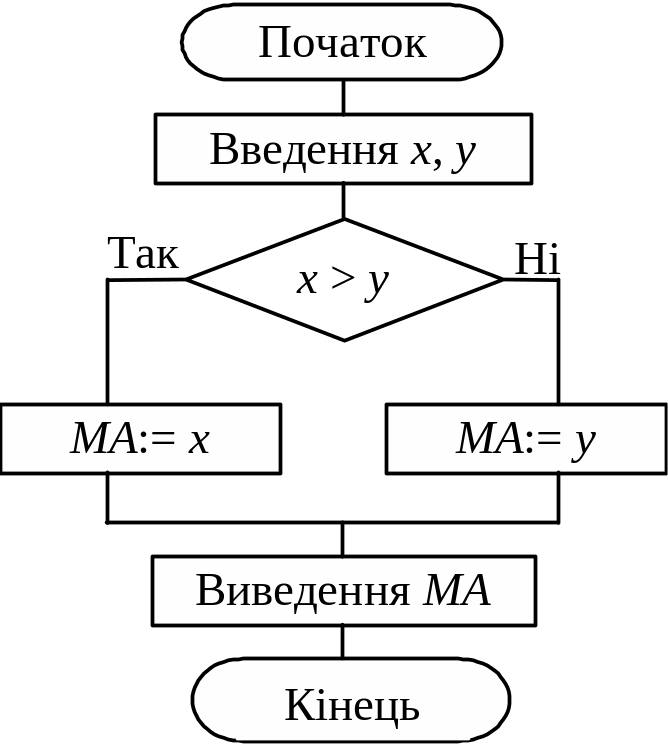
Рис. 5.5. Приклад простого розгалуженого алгоритму а)
Приклад 2б. Дано дійсні числа х, у, z. Обчислити min(x + y + z, xyz). (рис. 5.6):
Рис. 5.6. Приклад простого розгалуженого алгоритму б)
Складне розгалуження 5.3 відбувається послідовно, з відокремленням гілок за схемою (рис. 5.7).
Рис. 5.7 Схема складного розгалуженого процесу 5.3
Розгалужень може бути скільки завгодно.
Приклад 3. Дано три додатних числа x, y, z. Визначити, чи існує трикутник, що має сторони такої довжини. Алгоритм — на рис. 5.8.
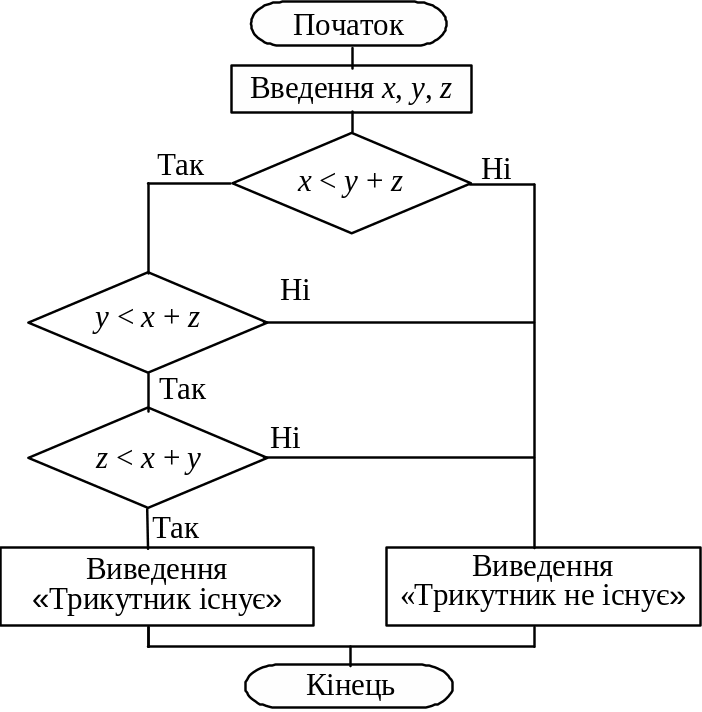
Рис. 5.8. Приклад складного розгалуженого алгоритму 5.3
Вже з цього прикладу видно, що збільшення кількості умов робить алгоритм більш заплутаним, він втрачає наочність, перевірити його правильність досить складно. У таких випадках необхідно перехід до будь-якої гілки розгалуженого алгоритму пов’язати з деякою змінною, кожне значення якої відповідатиме одній із гілок розгалуження, тобто одному з варіантів обробки інформації. Це можуть бути не тільки окремі значення, а й проміжки значень, до яких належатиме конкретне значення змінної. Тоді всі логічні блоки алгоритму об’єднуються в один блок аналізу цієї змінної, який матиме не два виходи, а стільки, скільки існує варіантів обробки.
Нехай К-змінна вибору варіантів може приймати значення а1, а2, ..., аn, ... Нехай існують варіанти обробки інформації, відповідні деяким переліченим значенням змінної чи їх сукупностям. Обов’язково необхідно передбачити варіант обробки, коли зна-чення змінної не належить до перелічених значень. Тоді розгалужений алгоритм матиме вигляд схеми 5.4 на рис. 5.9.
Рис. 5.9. Схема розгалуженого процесу вибору варіанта 5.4
Приклад 4. Визначити Y за умов:
Алгоритм визначення у матиме вигляд (рис. 5.10):
Рис. 5.10. Приклад розгалуженого алгоритму вибору варіанта 5.4
5.1.3. Прості циклічні процеси з параметром (5.5)
У нормальних алгоритмах Маркова передбачалася можливість багаторазової перевірки однієї і тієї самої умови (тобто повернення до того самого розпізнавача) та багаторазове виконання однієї чи декількох підстановок. Тим самим досягається компактність алгоритму, а також можливість розробки ефективної програми. Повторювану частину алгоритму називають тілом циклу (або циклом), а алгоритм, що його містить, — циклічним. Для побудови циклічного алгоритму необхідно:
— визначити всі дії, які необхідно виконати до входу в цикл, тобто провести підготовку циклу;
— визначити всі операції, які ввійдуть до циклу;
— скласти умову виходу з циклу.
Якщо в процесі перетворення інформації є змінна, значення якої змінюється за відомим правилом, або відомі межі її зміни, то можна визначити кількість циклів та організувати вихід із циклічного процесу. Таку змінну називають параметром циклу. Для організації циклічного процесу використовують лічильник циклів, пов’язаний із цим параметром. Схема такого процесу зображена на рис. 5.11.
Рис. 5.11. Схема простого циклічного процесу з параметром 5.5
Яку ж змінну можна використовувати як параметр циклу? Це може бути змінна, яка належить до оброблюваної інформації; це може бути індексна змінна, якщо оброблювана інформація є масивом, або коефіцієнти, що змінюються за законом арифметичної прогресії.
Приклад 1. Обчислити значення функції
для х = 1; 1.1; 1.2, ..., 2.
Тут за параметр циклу можна обрати змінну х, яка змінюється від х1 = 1 до х2 = 2 з кроком d = 0,1 (рис. 5.12).
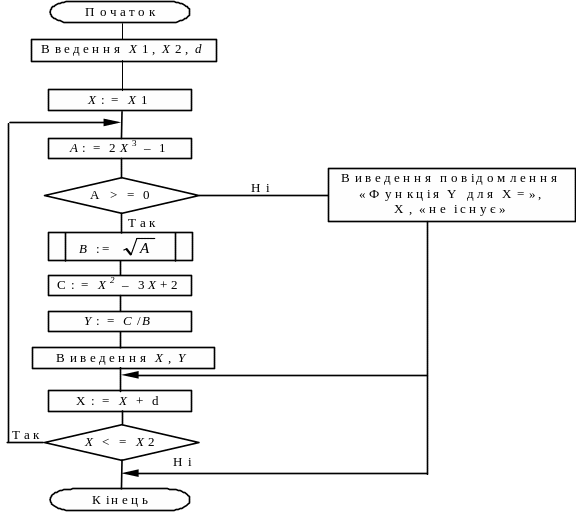
Рис. 5.12. Приклад 1 простого циклічного процесу з параметром 5.5
Приклад 2. Дано натуральне n та дійсне х. Обчислити у = sinx + 2 sinx2 + ... + nsinxn.
Тут цикл повторюється n разів, за параметр циклу можна взяти змінну i, яка прийматиме значення від 1 до n. S — сума, яку визначає алгоритм, а — аргумент функції sin, р — поточний доданок, b — значення функції sin. Якщо у циклі обчислюється послідовно сума, то її треба обнулити перед входом до циклу, якщо це добуток, то перед входом до циклу йому потрібно присвоїти значення 1. Це загальні правила. Алгоритм прикладу 2 зображено на рис. 5.13:
Рис. 5.13. Приклад 2 простого циклічного процесу з параметром 5.5
Приклад 3. Дано дійсні числа а1, а2 ... аn. Знайти їх середнє арифметичне значення.
Цикл повторюється n разів. Параметром буде і — індекс елемента у масиві, що змінюється від 1 до n із кроком 1. S — сума елементів; SA — середнє арифметичне (рис. 5.14)
Рис. 5.14. Приклад простого циклічного процесу з параметром 5.5