6. Решение задачи в MathCad

Для проверки правильной работоспособности программы, решим данное дифференциальное уравнение в рабочей среде MathCad, так же построим графики для трех методов решения: Эйлера модифицированного, Рунге-Кутта и общего решений.

• x1₀, h, x₁, f(x,y), y1₀ , x0, y0, c, у(x)– Начальные условия уравнения.

• x1_i, y1_i – Векторы значений решений уравнения методом Эйлера модифицированного.

• N – Количество точек решения.

• D (t,Y) := f(t,Y₀) - Специальная функция. Второй аргумент – вектор неизвестных значений функции.

• S - Решение в виде матрицы.

• T,Y – Вектора аргументов и значений искомой функции соответственно.

Рисунок 11 Проверка решения задачи в MathCad. Графики функций

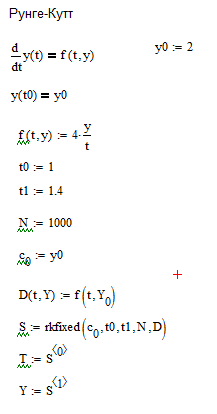
Продолжение рисунка 11 Проверка решения задачи в MathCad. Графики функций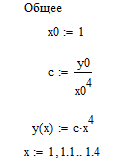

Продолжение рисунка 11 Проверка решения задачи в MathCad. Графики функций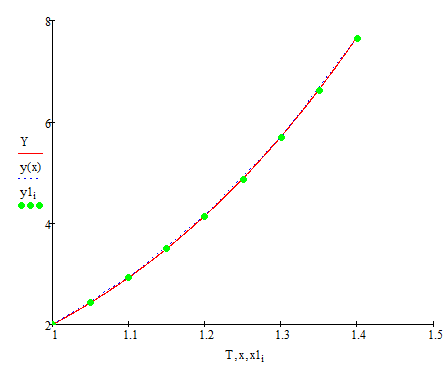

.

Исходя из того, что график программы (см. рисунок 12) и проверочный график выполненный в MathCad (см. рисунок 13) совпадают, можно сделать вывод, что проделанная работа по написанию программы была выполнена успешно. Основную цель курсовой работы считаю выполненной.

Заключение

Из двух методов (Эйлера модифицированного и Рунге-Кутта) по полученным результатам точнее по сравнению с общим решением оказался метод Рунге-Кутта. Так как в отличие от метода Эйлера модифицированного (где шаг делится на 2 отрезка), в методе Рунге-Кутта шаг делится на 4 отрезка, в результате чего погрешность метода становится меньше.

По завершению курсовой работы были выполнены все поставленные задачи: написана программа для решения данного дифференциального уравнения двумя численными методами в программе Visual Basic, проверено решение с помощью приложения MathCad, произведено сравнение полученных разными методами результатов с общим решением.

Список используемых источников

1. Демидович Б.П., Марон И.А., Шувалова Э.З., Численные методы анализа. – М.: Физматгиз, 1963.-400 с.

2. Иванова Т.П., Пухова Г.В. Вычислительная математика и программирование, М.:Просвещение, 1978.-320 с.

3. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике: Учеб. Пособие для втузов. – М.: Высшая школа, 1983.-208 с.

4. Браун С. Visual Basic 6. Учеб. курс. –СПб.: Питер, 2006.-574 с.