4 Форма программы
В
результате изучения методов решения
дифференциальных уравнений, составления
их алгоритмов, была написана программа
для решения и построения графика
дифференциального уравнения
Программа написана в программной среде Visual Basic.
Вид программы для ввода данных:
Text2
Labe31
Command1
Text1
Label10
Labe91
Label4
Labe71
Labe41
Text3
Text4
MSFlexGrid16
Labe21
Label1
Label6
Picture1
Labe51
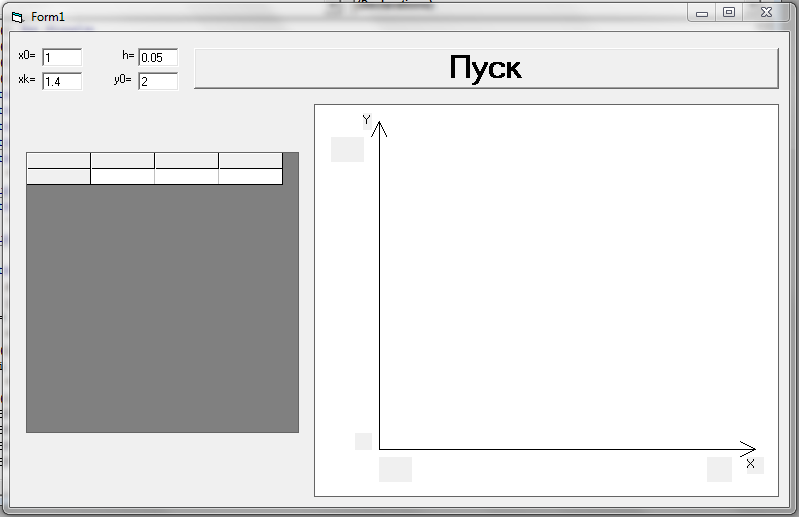
Рисунок 9 Исходный вид программы
Text1, Text2, Text3, Text4 – поля для ввода входных параметров
MSFlexGrid1 – таблица, для вывода полученных результатов
PictureBox1 – поле для построения графика
Label5, Label6, Label7, Label8 – поля для max и min на осях y и x
После ввода начальных условий в поля Text1..Text4 и нажатии на кнопку пуск, программа заполняет массив данных MSFlexGrid1, и, основываясь на данные массива, строит график в поле PictureBox1. В полях Label5..Label8 программа указывает max и min значения на осях X и Y.
Итоговый вид программы с предоставленным решением и графиком:
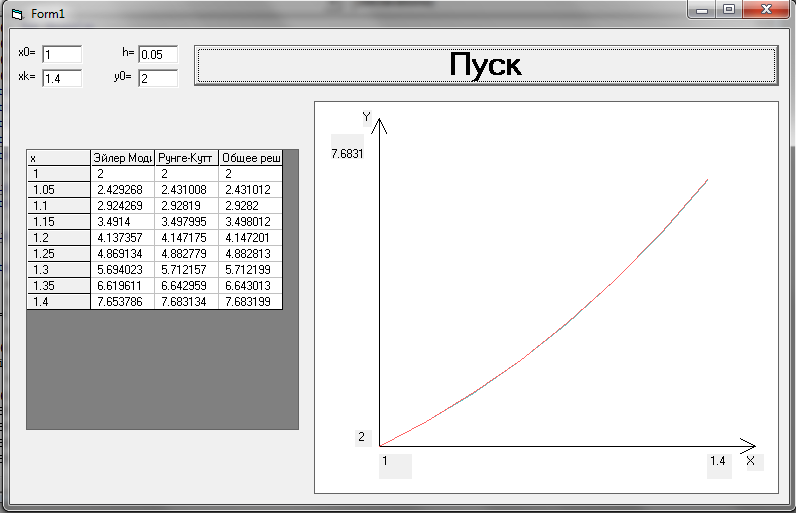
Рисунок 10 Итоговый вид с предоставленным решением и графиком
5 Листинг программы
Dim x() As Single
Dim y() As Single
Dim g() As Single
Dim t() As Single
Private n, i As Integer
Private xk, x0, kx, ky As Single
Private k, k1, k2, k3, k4 As Single
Private h, max, min, y0 As Single
Private Function f(a, b As Single) As Single
f = 4 * b / a
End Function
Private Function v(x As Single) As Single
v = x ^ 4 * y0 / x0 ^ 4
End Function
Private Sub EilerMod()
ReDim x(n)
ReDim y(n)
y(0) = y0
For i = 0 To n
x(i) = x0 + h * i
Next i
For i = 0 To n - 1
y(i + 1) = y(i) + h * f(x(i) + h / 2, y(i) + h / 2 * f(x(i), y(i)))
MSFlexGrid1.TextMatrix(1, 0) = Str(x0)
MSFlexGrid1.TextMatrix(i + 2, 0) = Str(x(i + 1))
MSFlexGrid1.TextMatrix(1, 1) = Str(y0)
MSFlexGrid1.TextMatrix(i + 2, 1) = Str(y(i + 1))
Next i
End Sub
Private Sub Rynge_Kytt()
ReDim g(n)
g(0) = y0
For i = 0 To n
x(i) = x0 + h * i
Next i
For i = 0 To n - 1
k1 = h * f(x(i), g(i))
k2 = h * f(x(i) + h / 2, g(i) + k1 / 2)
k3 = h * f(x(i) + h / 2, g(i) + k2 / 2)
k4 = h * f(x(i) + h, g(i) + k3)
k = (k1 + 2 * k2 + 2 * k3 + k4) / 6
g(i + 1) = g(i) + k
MSFlexGrid1.TextMatrix(i + 2, 2) = Str(g(i + 1))
MSFlexGrid1.TextMatrix(1, 2) = Str(g(0))
Next i
End Sub
Private Sub Obshee()
ReDim t(n)
For i = 0 To n
t(0) = y0
x(i) = x0 + h * i
t(i) = v(x(i))
MSFlexGrid1.TextMatrix(i + 1, 3) = Str(t(i))
Next i
End Sub
Private Sub Command1_Click()
x0 = Val(Text1.Text)
xk = Val(Text2.Text)
h = Val(Text3.Text)
y0 = Val(Text4.Text)
n = (xk - x0) / h
MSFlexGrid1.Rows = n + 2
MSFlexGrid1.TextMatrix(0, 0) = "x"
MSFlexGrid1.TextMatrix(0, 1) = "Эйлер Модиф."
MSFlexGrid1.TextMatrix(0, 2) = "Рунге-Кутт"
MSFlexGrid1.TextMatrix(0, 3) = "Общее решение"
Label6.Caption = Str(x0)
Label5.Caption = Str(xk)
EilerMod
Rynge_Kytt
Obshee
max = y0
min = y0
For i = 0 To n
If y(i) > max Then
max = y(i)
End If
If y(i) < min Then
min = y(i)
End If
If g(i) > max Then
max = g(i)
End If
If g(i) < min Then
min = g(i)
End If
If t(i) > max Then
max = t(i)
End If
If t(i) < min Then
min = t(i)
End If
Next i
Label4.Caption = Str(max)
Label7.Caption = Str(min)
kx = (6600 - 960) / (xk - x0)
ky = (5160 - 240) / (max - min)
Picture1.Cls
For i = 1 To n - 1
X1 = 960 + Round(kx * (x(i - 1) - x0))
X2 = 960 + Round(kx * (x(i) - x0))
Y1 = 5160 - Round(ky * (y(i - 1) - min))
Y2 = 5160 - Round(ky * (y(i) - min))
Picture1.Line (X1, Y1)-(X2, Y2), RGB(100, 200, 200)
X1 = 960 + Round(kx * (x(i - 1) - x0))
X2 = 960 + Round(kx * (x(i) - x0))
Y1 = 5160 - Round(ky * (g(i - 1) - min))
Y2 = 5160 - Round(ky * (g(i) - min))
Picture1.Line (X1, Y1)-(X2, Y2), RGB(400, 300, 300)
X1 = 960 + Round(kx * (x(i - 1) - x0))
X2 = 960 + Round(kx * (x(i) - x0))
Y1 = 5160 - Round(ky * (t(i - 1) - min))
Y2 = 5160 - Round(ky * (t(i) - min))
Picture1.Line (X1, Y1)-(X2, Y2), RGB(500, 100, 100)
Next i
End Sub
Private Sub Form_Load()
Command1.FontBold = True
Command1.FontSize = 25
End Sub