2. 4 Метод Эйлера модифицированный
Для уменьшения погрешности вычислений часто используется модифицированный метод Эйлера. Этот метод имеет так же следующие названия: метод Эйлера-Коши или метод Рунге-Кутта второго порядка точности.
Пусть дано дифференциальное уравнение первого порядка
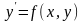
с начальным условием:
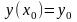
Выберем шаг h и введём обозначения:
xi = x0 + i * h и yi = y(xi), где i = 0, 1, 2, ...,
xi - узлы сетки,
yi - значение интегральной функции в узлах.
При использовании модифицированного метода Эйлера шаг h делится на два отрезка.
Иллюстрации к решению приведены на рисунке 2.
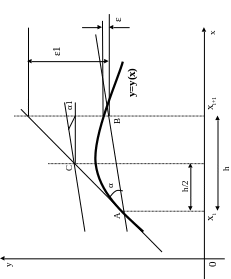
Рисунок 2 Метод Эйлера модифицированный.
Проведем решение в несколько этапов:
Обозначим точки: А(хi, yi), C(xi + h/2, yi + h/2 ∙ f(xi, yi)) и B(xi+1, yi+1).
Через точку А проведем прямую под углом α, где tg α = f(xi, yi).
На этой прямой найдем точку С(хi + h/2, yi + h/2 ∙ f(xi, yi)).
Через точку С проведем прямую под углом α1, где
.
Через точку А проведем прямую, параллельную последней прямой.
Найдем точку B(xi+1, yi+1). Будем считать B(xi+1, yi+1) решением дифференциального уравнения при х = xi+1.
После проведения вычислений, аналогичных вычислениям, описанным в методе Эйлера, получим формулу для определения значения уi+1:
.
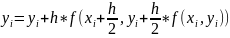Модифицированный метод Эйлера дает меньшую погрешность. На рисунке 2 это хорошо видно. Так величина εl характеризует погрешность метода Эйлера, а ε - погрешность метода Эйлера модифицированного.
Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным приведена на рисунке 3.
Входные параметры:
Х0, XК - начальное и конечное значения независимой переменной.
Y0 – значение y0 из начального условия y(x0)=y0.
N - количество отрезков разбиения.
Выходные параметры:
Y - массив значений искомого решения в узлах сетки.
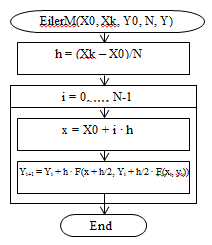
Рисунок 3 Блок-схема процедуры решения дифференциального уравнения методом Эйлера модифицированным.
2.5 Метод Рунге-Кутта 4 порядка
Для большего уменьшения погрешности используется метод Рунге-Кутта четвёртого порядка точности (метод Рунге-Кутта).
Пусть
дано дифференциальное уравнение первого
порядка
с
начальным условием
.
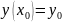Выберем шаг h
и
введём обозначения:
и
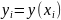, где
i=0,1,2,… xi—
узлы сетки, yi
значение интегральной функции в узлах
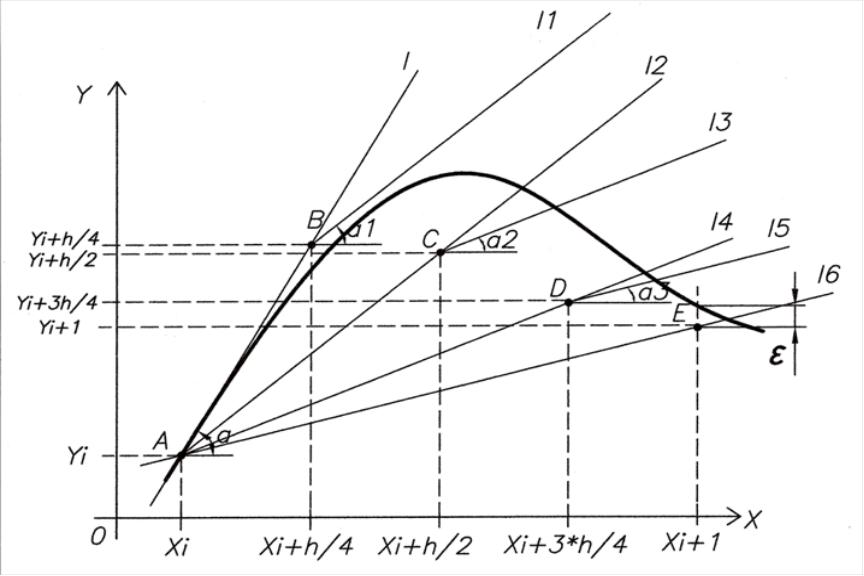
Рисунок 4 Графическое изображение метода Рунге-Кутта 4-го порядка
При
использовании модифицированного метода
Рунге-Кутта шаг h
делится на четыре отрезка. Согласно
этому методу, последовательные значения
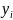исходной функции y
определяются по формуле:
,
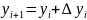где
,
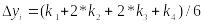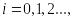
А
числа
на каждом шаге вычисляются по формулам:
Это явный четырёхэтапный метод четвёртого порядка точности.
Метод Рунге-Кутта даёт погрешность меньше, чем методы Эйлера и Эйлера модифицированного.
Все методы Рунге-Кутта легко программируются и обладают значительной точностью.
Блок-схема процедуры решения дифференциального уравнения методом Рунге-Кутта приведена на рисунке 5.
Входные параметры:
Х0, XК - начальное и конечное значения независимой переменной.
Y0 – значение y0 из начального условия y(x0)=y0.
N - количество отрезков разбиения.
Выходные параметры:
Y - массив значений искомого решения в узлах сетки.
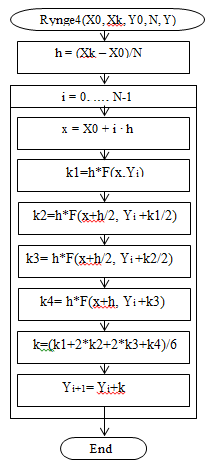
Рисунок 5 Блок-схема процедуры решения дифференциального уравнения методом Рунге-Кутта
3 Блок-схемы решения задачи
1 Блок-схема общего решения
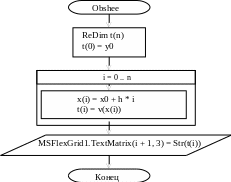
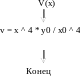
Рисунок 6 Блок-схема общего решения
Данная процедура находит общее решение заданного дифференциального уравнения.
x – массив корней x
t – массив корней y
v – формула общего решения, с выраженным и подставленным “c”
i – счетчик
3
.
2 Блок-схема функции
Рисунок 7 Блок-схема функции
3. 3 Блок-схема программы
Рисунок
8 Блок-схема программы
Продолжение
рисунка 8 Блок-схема программы
Продолжение
рисунка 8 Блок-схема программы