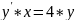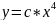Федеральное агентство связи

ГОУ ВПО «Сибирский государственный университет

Телекоммуникаций и информатики»

Уральский технический институт связи и информатики (филиал)

Курсовая работа

по информатике на тему

«Визуализация численных методов. Решение обыкновенных дифференциальных уравнений»

Вариант 12

Выполнил студент гр. СЕ-01 Мартьянов В.Е.

Проверил: Сонина Е.Ю.

Екатеринбург

2011 г.

Содержание

Введение………………………………………………………………….3

1 Постановка задачи…………………………………………………….4

2 Описание методов решения…………………………………………..5

2. 1 Суть задачи………………………………………………………….5

2. 2 Геометрический смысл задачи…………………………………….5

2. 3 Численные методы решения задачи Коши……………………….6

2. 4 Метод Эйлера модифицированный……………………………….7

2. 5 Метод Рунге-Кутта 4-го порядка………………………………….8

3 Алгоритм решения задачи…………………………………………...11

3. 1 Алгоритмы подпрограмм.………………………………………....11

3. 2 Алгоритм функции…………………………………………………14

3. 3 Алгоритм программы………………………………………………14

4 Форма программы…………………………………………………….17

5 Листинг программы…………………………………………………..19

6 Решение задачи в MathCad…………………………………………..22

Заключение………………………………………………………………24

Список используемых источников……………………………………25

Введение

При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде дифференциальных уравнений связывающих независимую переменную, искомую функцию и ее производные. Например, исследуя полученные дифференциальные уравнения вместе с дополнительными условиями, можно получить сведения о происходящем явлении, иногда можно узнать его прошлое и будущее. Изучение математической модели математическими методами позволяет не только получить качественные характеристики физических явлений и рассчитать с заданной степенью точности ход реального процесса, но и дает возможность проникнуть в суть физических явлений, а иногда предсказать и новые физические эффекты. Бывает, что сама природа физического явления подсказывает и подходы, и методы математического исследования. Критерием правильности выбора математической модели является практика, сопоставление данных математического исследования с экспериментальными данными. Не всегда удается решить дифференциальное уравнение без помощи компьютера, поэтому создание все лучших и удобных программ для решения уравнений всегда будет являться актуальным вопросом.

Целью данной курсовой работы является решение дифференциального уравнения двумя численными методами: методом Эйлера модифицированного (или Рунге-Кутта 2 порядка точности) и методом Рунге-Кутта 4 порядка точности.

Для достижения цели поставлены следующие задачи:

• Написать программу для решения данного дифференциального уравнения двумя численными методами в программе Visual Basic.

• Проверить решение с помощью приложения MathCad.

• Сравнить полученные разными методами результаты с общим решением.

1 Постановка задачи

Решить методами Рунге-Кутта и Эйлера модифицированного задачу Коши для дифференциального уравнения 1-го порядка на отрезке [X₀; X_k] с шагом h и начальным условием: Y(X₀) = Y₀.

Ответ должен быть получен в виде таблицы результатов:

X	Y(1)	Y(2)	YT
X0	Y0(1)	Y0(2)	Y(X0)
X1	Y1(1)	Y1(2)	Y(X1)
…	…	…	…
Xk	Yk(1)	Yk(2)	Y(Xk)

Y⁽¹⁾, Y⁽²⁾ – решения, полученные различными численными методами, Y^T – точное решение дифференциального уравнения.

Возможно представление результатов решения не в виде таблицы, а в виде списков.

Данные таблицы визуализировать на форме в виде графиков.

Перед вычислением последнего столбца таблицы результатов необходимо из начальных условий вычесть значение коэффициента c, используемого в общем решении.

Дифференциальное уравнение	X0	Xk	h	Y0	Общее решение
	1	1,4	0,05	2