- •Лекція тема заняття. Моделі та методи лінійного програмування, їх застосування за допомогою табличного процесору ms excel
- •1. Модели и моделирование.
- •2. Понятие линейного программирования. Виды задач линейного программирования
- •3. Модель линейного программирования, её представление в электронных таблицах ms excel.
- •Основные этапы создания модели линейного программирования в Excel:
- •4. Использование надстройки поиск решения.
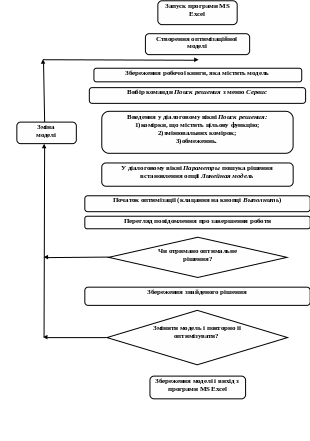
- •Алгоритм роботи з надбудовою Поиск решения.
- •5. Решение задачи линейного программирования при помощи программы ms excel.
Алгоритм роботи з надбудовою Поиск решения.
5. Решение задачи линейного программирования при помощи программы ms excel.
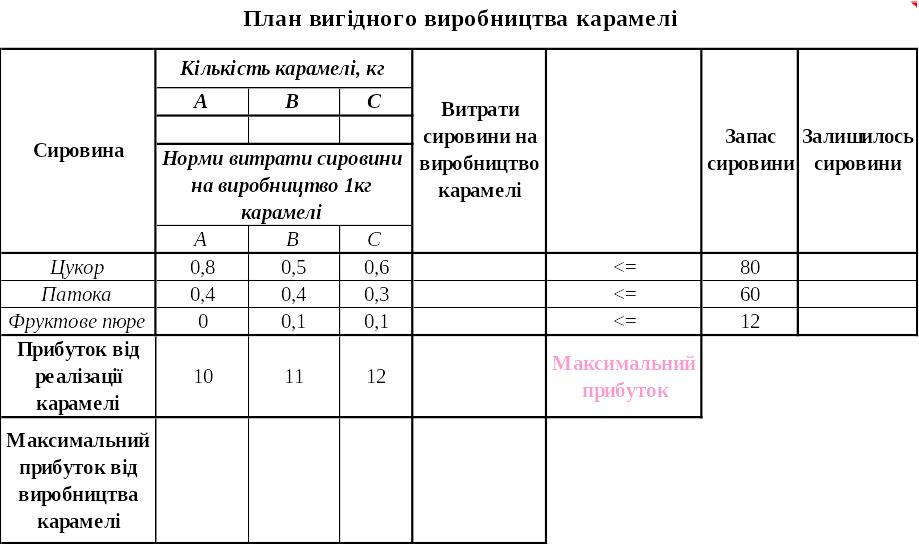
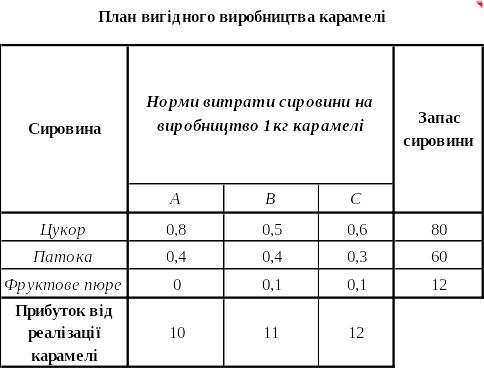
Пример. Кондитерский цех для изготовления трех видов карамели А, В, С использует три основных вида сырья: сахар, патоку и фруктовое пюре. Нормы затрат сахара на изготовление 1кг карамели каждого вида соответственно уровни: 0,8кг; 0,5кг; 0,6кг; патоки – 04кг; 0,4кг; 0,3кг; фруктового пюре – 0кг; 0,1кг; 0,1кг. Конфеты можно производить в любых количествах (реализация обеспечена), но запас сырья ограниченный: запасы сахара – 80кг, патоки – 60кг, фруктового пюре – 12кг. Прибыль от реализации 1кг карамели вида А составляет 10грн., вида В – 11грн., вида С – 12грн.
Таблица 1
Определить план производства карамели, которая обеспечивает максимальную прибыль от деятельности кондитерского цеха.
Решение.
|
По данному условию задачи сформулируем задачу линейного программирования то есть построим математическую модель. Обозначим: x1 – количество карамели вида А, x2 – количество карамели вида В, x3 – количество карамели вида С. Карамель выпускается ежедневно. Найти наибольшее значение целевой функции F = 10x1 + 11x2 +12x3 > max, при ограничениях 0,8x1 + 0,5x2 +0,6x3 80 0,4x1 + 0,4x2+0,3x3 60 0,1x2+0,1x3 12; x1 ≥ 0, x2≥ 0, x3≥ 0. Подчеркнем, что каждое неравенство в системе функциональных ограничений отвечает в этом случае тому или другому производственному участку, а именно: первое – участку А, второе – участку В, третье – участку С. |
|
Выходные данные задачи об использовании производственных ресурсов. Таблица 1.
Рисунок 1 Режим проверки формул
|
|
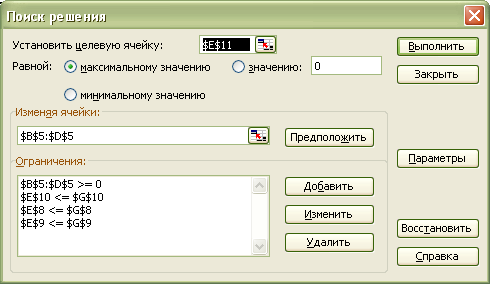
Рисунок 2 Диалоговое окно Поиск решения В диалоговом окне Поиск решения в поле Установит целевую ячейку делаем ссылку на ячейку $E$11, в которой находится формула, для оптимизации модели. Для того, чтобы максимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение Максимальному значению. В поле ввода Изменяя ячейки введите адреса ячеек, которые изменяют свои значения, разделяя их запятыми. Для этого делаем ссылку на ячейки $B$5:$D$5. В поле Ограничения введите все ограничения, которые налагаются на поиск решения. Для этого нажимаем кнопку Добавить и появится окно Добавить ограничения где нужно ввести ограничение. Если при вводе ограничений возникает необходимость в замене или удалении внесенных ограничений, то нажмите кнопки Изменить или Удалить.
Рисунок 3 Оптимальное решение Вывод: как видно из решения, оптимальный план выпуска продукции предусматривает изготовление 25кг конфет А и 120кг конфет В. Конфеты С вообще невыгодно производить. Прибыль будет составлять 1570грн. |