
- •1. Линейные вычислительные процессы. Построение диаграмм и графиков.
- •2. Разветвляющиеся вычислительные процессы
- •8. Заданы числа X и y и область d. Рассчитать величину z по формуле:
- •3. Циклические вычислительные процессы
- •3.1. Обработка рекуррентных выражений
- •3.2. Вычисление суммы элементов последовательности
- •Работа с массивами и записями
3. Циклические вычислительные процессы
3.1. Обработка рекуррентных выражений
1. Элементы
последовательности вычисляются по
формуле
![]() Составить программу определения для
заданного
Составить программу определения для
заданного
![]() такого
n, при котором
такого
n, при котором
![]() >
C, где С - большое число и |x|>
1.
>
C, где С - большое число и |x|>
1.
2. Составить
программу вычисления
![]() c точностью eps, используя итерационную
формулу
c точностью eps, используя итерационную
формулу
![]() , причем 0.5 =< x < 1. Принять
, причем 0.5 =< x < 1. Принять
![]() и
eps=0.001.
и
eps=0.001.
3. Функцию 1/x можно вычислить с помощью следующих рекуррентных выражений:
![]() и
и
![]() ,
с начальными условиями a =1, c = 1-x. Для 0 <
x < 2 составить программу вычисления
1/x с точностью eps=0.001.
,
с начальными условиями a =1, c = 1-x. Для 0 <
x < 2 составить программу вычисления
1/x с точностью eps=0.001.
4. Даны действительные
числа x и eps (eps=0.001). Последовательность
![]() ,...
образована по следующему закону:
,...
образована по следующему закону:
![]() ,
i=1,2,.... Найти первый элемент
,
i=1,2,.... Найти первый элемент![]() ,
для которого
,
для которого![]() .Принять
eps = 0.001 и
.Принять
eps = 0.001 и
![]()
5. Составить
программу решения уравнения
![]() с
помощью итерационной формулы
с
помощью итерационной формулы
![]() ,
здесь
,
здесь![]() производная
от f(x). Вычисления заканчиваются при
производная
от f(x). Вычисления заканчиваются при![]() .
Начальное значение
и точность eps считать известными.
.
Начальное значение
и точность eps считать известными.
6. Составить
программу вычисления корня m-й степени
из числа х по итерационной формуле
![]() .
Считать, что
.
Считать, что
![]() и итерации заканчиваются при
и итерации заканчиваются при![]() .
.
7. Определить
номер итерации, при котором для
итерационного процесса
![]() выполняется условие
,
принять для отладки eps = 0.001 и x=25.
выполняется условие
,
принять для отладки eps = 0.001 и x=25.
8. Составить
программу для вычисления
![]() c
использованием итерационной формулы
c
использованием итерационной формулы![]() .
Вычисления заканчиваются при
.
Принять
.
Вычисления заканчиваются при
.
Принять
![]() и
eps=0.001.
и
eps=0.001.
9. Составить
программу для вычисления числа![]() ,
пользуясь рядом Грегори
,
пользуясь рядом Грегори
![]() с точностью
eps=0.001.
с точностью
eps=0.001.
10. Составить
программу определения n-го члена
последовательности Фибоначчи, при
котором![]() ,
где C - большое число.
,
где C - большое число.
11. Даны положительные
числа a и eps. В последовательности,
образованной по закону![]() ,
найти первое значение
,
найти первое значение
![]() ,
для которого выполнено условие
.
Принять eps = 0.001 и
,
для которого выполнено условие
.
Принять eps = 0.001 и![]() .
.
12. Для
последовательности, образованной по
формуле
![]() ,
i=1,2,3,...,
S0=1
и |x|
< 1, найти такое i, при котором
,
i=1,2,3,...,
S0=1
и |x|
< 1, найти такое i, при котором
![]() ,
eps = 0.001.
,
eps = 0.001.
13. Дано действительное
число a > 0. Для последовательности,
образованной по закону![]() ,
определить такое i, при котором
.
Начальное значение
вычисляется
по формуле
,
определить такое i, при котором
.
Начальное значение
вычисляется
по формуле
![]()
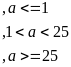
14. Даны a=2, b=3,
eps=0,001 и
![]() .
Определить по рекуррентной формуле
.
Определить по рекуррентной формуле
![]() при
при
![]() такие n и
такие n и
![]() ,
при которых
,
при которых
![]() .
.
15. Составить
программу для определения номера
итерации, при котором значение
,
вычисляемое по рекуррентной формуле
![]()
![]() ,
будет удовлетворять неравенству
.
Принять x=3693,
,
будет удовлетворять неравенству
.
Принять x=3693,
![]() и eps=0,001.
и eps=0,001.
16. Определить
![]() по
формуле
по
формуле
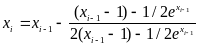 при котором
Принять
при котором
Принять
![]() ,
и eps=0.001.
,
и eps=0.001.
17. Определить
по формуле
![]() ,
при котором
.
Принять x=9.1,
,
при котором
.
Принять x=9.1,
![]() =
x/3.
=
x/3.
18. Определить, при каком значении i величина числа , рассчитанная по формуле
![]() , будет отличаться
от истинного значения не более чем на
одну тысячную. Истинное значение числа
принять 3.141592
, будет отличаться
от истинного значения не более чем на
одну тысячную. Истинное значение числа
принять 3.141592
19. Пусть
![]() вычисляется
по формуле
вычисляется
по формуле
![]() !,
где x- заданное число и |x|<
1. Определить рекуррентное выражение
для вычисления
через
!,
где x- заданное число и |x|<
1. Определить рекуррентное выражение
для вычисления
через
![]() и составить программу определения
такого i, при котором
.Принять
eps = 0.001. В программе предусмотреть защиту
от ввода значений х, не удовлетворяющих
заданному ограничению.
и составить программу определения
такого i, при котором
.Принять
eps = 0.001. В программе предусмотреть защиту
от ввода значений х, не удовлетворяющих
заданному ограничению.
20. Для вещественного
числа a определить величину
![]() .
Корни
.
Корни
![]() вычислять с точностью eps=0.001 по
итерационнойїџ формуле
вычислять с точностью eps=0.001 по
итерационнойїџ формуле
![]() ,
приняв за ответ приближение
,
приняв за ответ приближение
![]() ,
при котором
,
при котором
![]() .
.
21. Для заданного
x с точностью eps=0.001 вычислить
![]() . Для вычисления корней использовать
следующее выражение:
. Для вычисления корней использовать
следующее выражение:
![]() , при |x|<
1 и a > 0.
, при |x|<
1 и a > 0.
22. Даны натуральное
число k и действительное число a.
Последовательность
![]() ...
образована по закону
...
образована по закону
![]() Найти первое значение
,
для которого
Найти первое значение
,
для которого
![]() .
.
23. Определить
рекуррентную формулу для вычисления
![]()
![]() .
Составить программу расчета i по
полученной рекуррентной формуле, при
котором
.
Составить программу расчета i по
полученной рекуррентной формуле, при
котором
![]() .
Принять |x|<
1 и eps = 0.001.
.
Принять |x|<
1 и eps = 0.001.
24. Составить
программу вычисления интеграла
![]() с заданной точностью eps=0.001 по формуле
трапеций
с заданной точностью eps=0.001 по формуле
трапеций
![]() .
Значение n на каждой итерации должно
удваиваться
.
Значение n на каждой итерации должно
удваиваться
![]() и
и
![]() где h=(b-a)/n
где h=(b-a)/n
25. Пусть
вычисляется по формуле
![]() .
Вычислять произведение
.
Вычислять произведение
![]() до
тех пор, пока не выполнится условие
.
Принять
и
до
тех пор, пока не выполнится условие
.
Принять
и
![]() равными
1.
равными
1.
