3.5. Інтегрування функцій, раціонально залежних від тригонометричних

Домовимось позначати - раціональну функцію, залежну від , якщо вона утворена з цих тригонометричних функцій та сталих за допомогою раціональних алгебраїчних дій.

1) Інтеграли виду приводяться до інтегралів від раціональної функції нового аргументу підстановкою

, яка називається універсальною.

При цьому використовуються формули:

, , , .

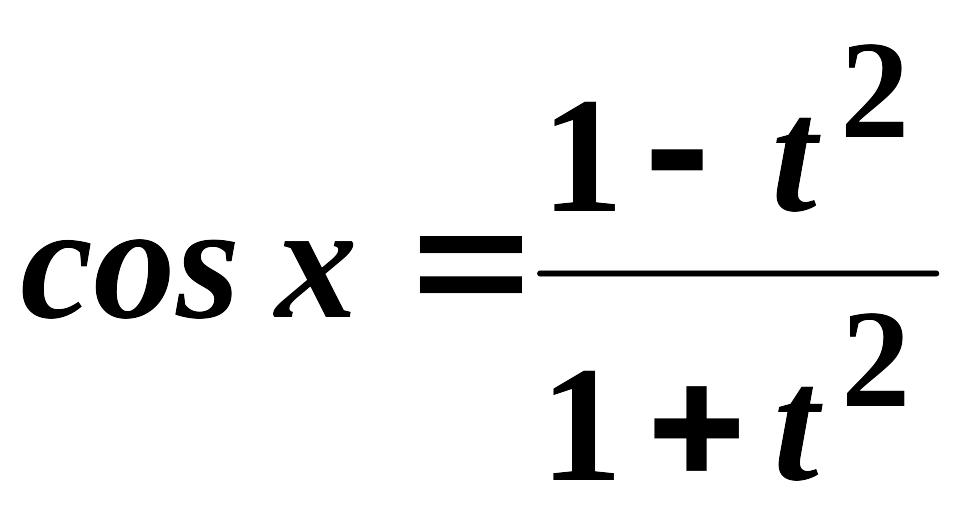Варто помітити, що недоліком цієї підстановки є той факт, що її використання в багатьох випадках зводить вихідний інтеграл до інтегралу від раціонального дробу з великими степенями. Тому в багатьох випадках користуються іншими підстановками . Наведемо деякі з них:

а) , тобто підінтегральна функція непарна відносно . Використовується підстановка , тоді , ;

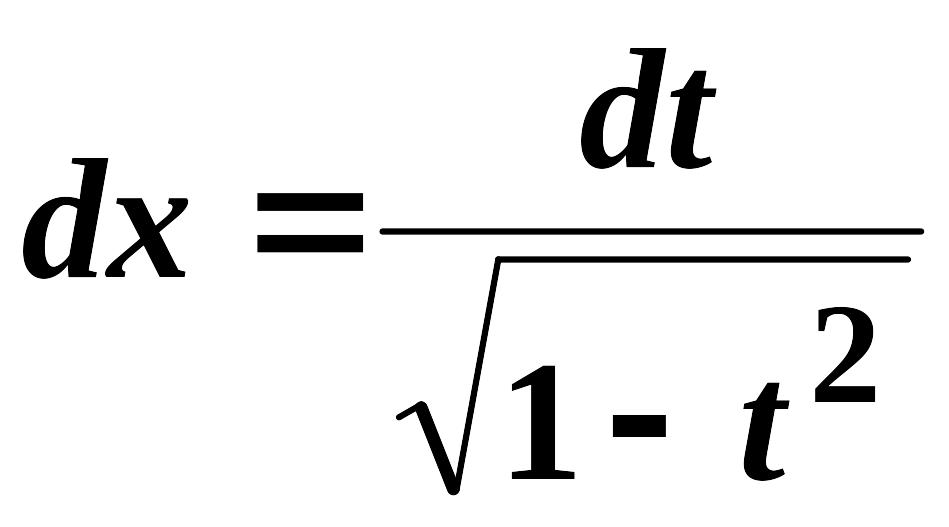б) - підінтегральна функція непарна відносно .

Використовується підстановка , тоді , ;

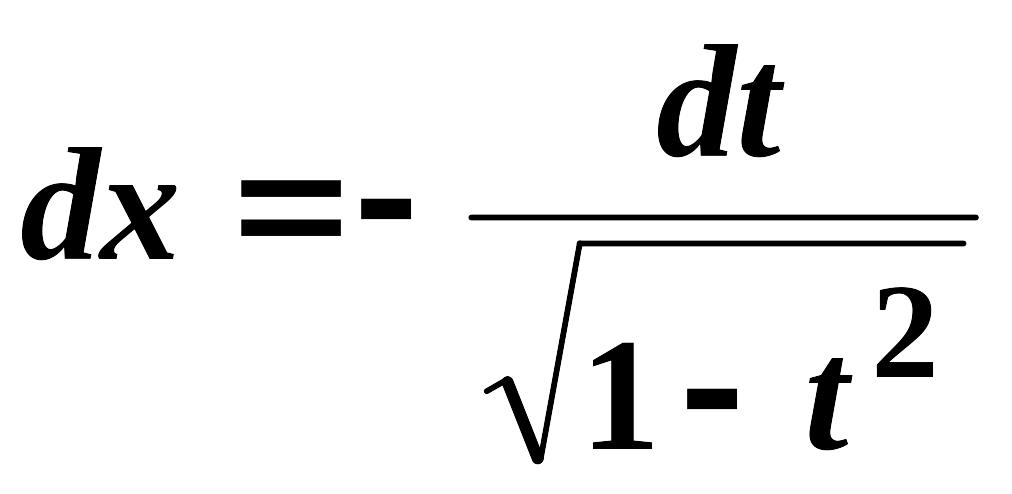в) , в якому підінтегральна функція парна відносно і одночасно, раціоналізується за допомогою підстановки . При цьому використовуються формули:

, , , ;

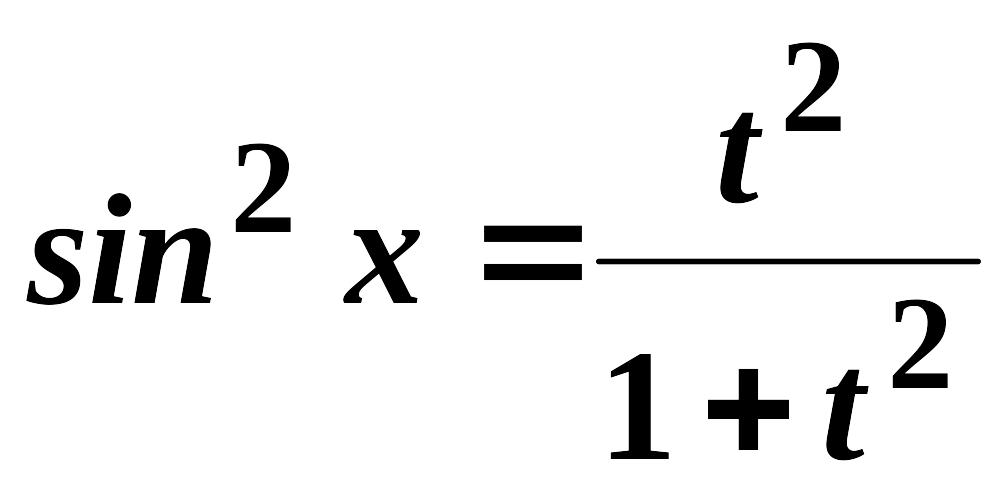г) . Тут підінтегральна функція залежить раціональним образом тільки від . Слід застосовувати підстановку , тоді , .

2) Інтеграли виду обчислюються за допомогою таких підстановок:

а) якщо - ціле додатне непарне число: ;

б) якщо - ціле додатне непарне число: ;

в) якщо та - цілі додатні парні числа: використовуються формули пониження степеня

, ;

г) якщо та - цілі парні числа, але хоч одне з них від’ємне: ;

д) якщо та - цілі непарні числа і від’ємні: .

3) Інтеграли виду , , обчислюються за допомогою тригонометричних формул:

,

,

.

3.6. Інтегрування деяких іраціональних функцій

Насамперед зауважимо, що інтеграл від іраціональної функції не завжди обчислюється в скінченному вигляді. Розглянемо деякі типи таких інтегралів, які за допомогою певної підстановки можна звести до інтеграла від раціональної функції, а отже, знайти його.

1) Інтеграли виду 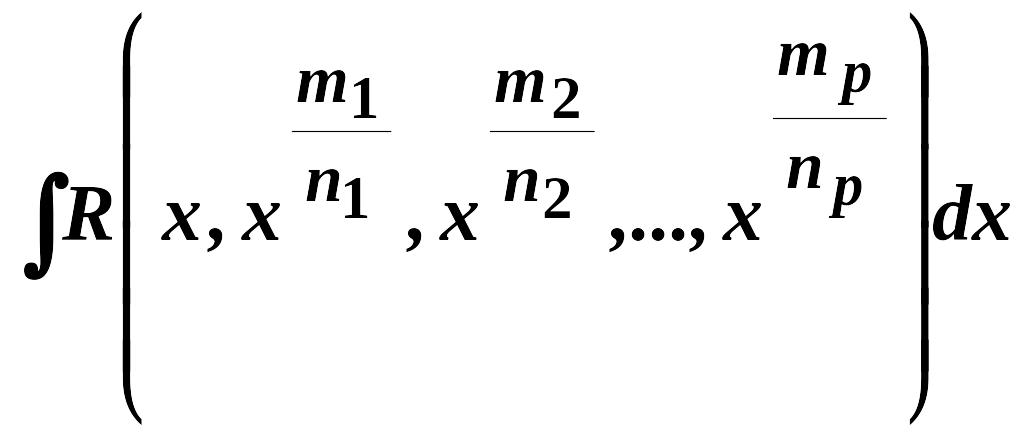, де > , - натуральні числа, обчислюються за допомогою підстановки , де - спільний знаменник дробів .

2) Інтеграли виду ,

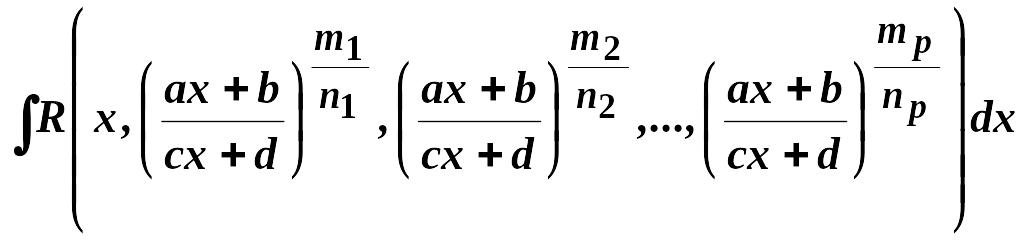де - дійсні числа, причому (бо у противному випадку відношення є сталим і підінтегральна функція в цьому разі є раціональною функцією від ) за допомогою підстановки зводяться до інтегралів від раціональної функції змінної .

3) а) Інтеграли виду 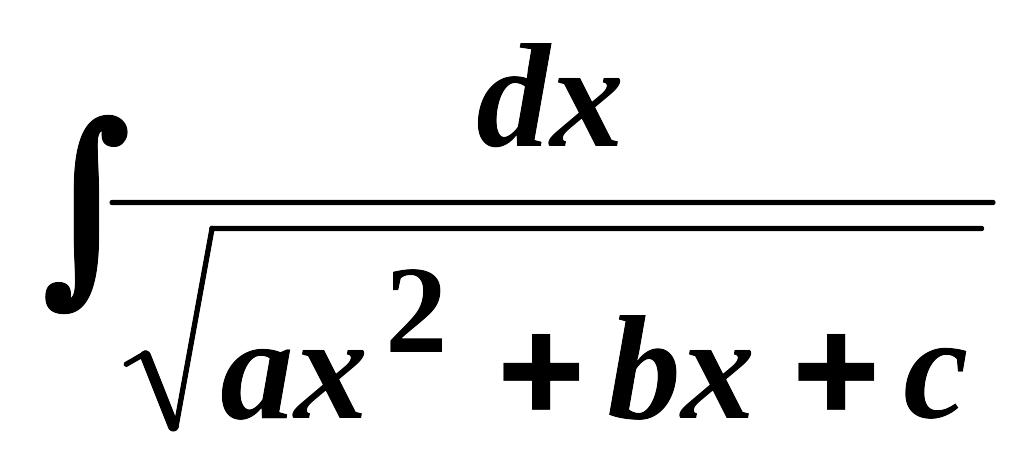вилученням повного квадрату під радикалом зводяться до табличних інтегралів:

, ;

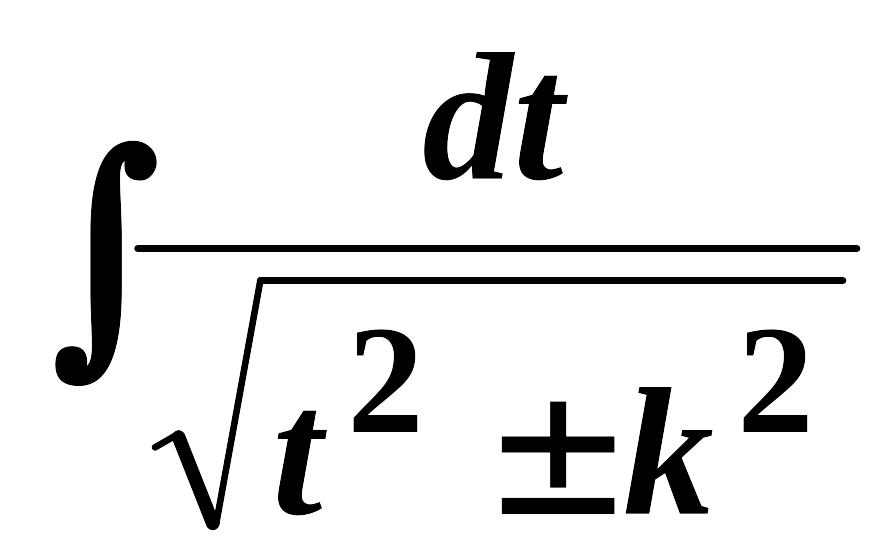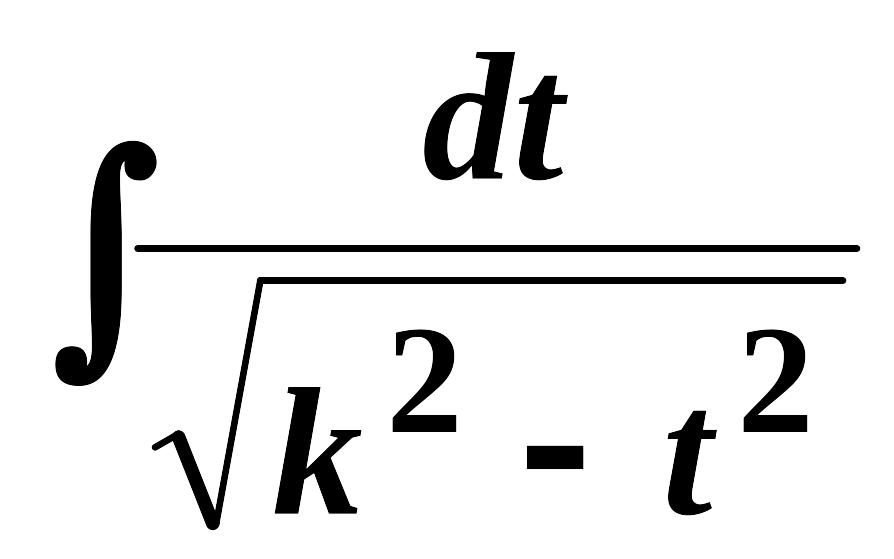б) інтеграли виду 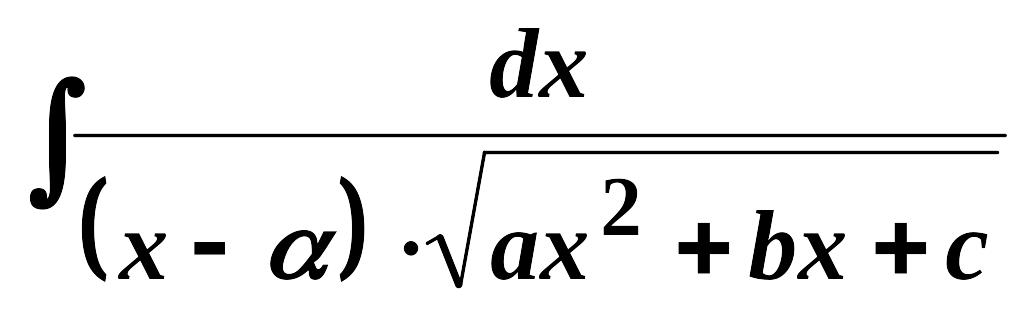за допомогою підстановки зводяться до інтегралів попереднього виду.

4) Для перелічених нижче видів іраціональностей використовуються тригонометричні підстановки, що дозволяють прийти до інтегралів від тригонометричних функцій і .

Розглянемо випадки:

а) для інтегралів виду застосовується підстановка або ;

б) для інтегралів виду застосовується підстановка або ;

в) для інтегралів виду підстановка або дає змогу позбутися іраціональності.

17