3.2. Метод підстановки (заміни змінної)

Заміна змінної у невизначеному інтегралі виконується за допомогою підстановок двох типів:

1. Інтеграл зображають у вигляді:

,

де функція має обернену функцію і для функції відома первісна .

Тоді .

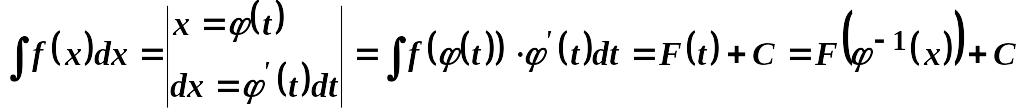2. Інтеграл записують у вигляді

,

в якому для функції відома первісна .

Тоді

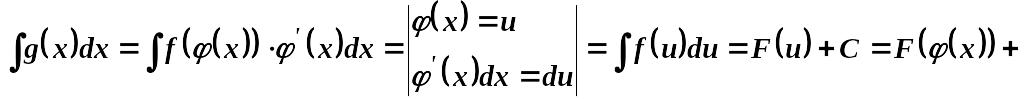
В обох випадках досягається мета спростити вихідний інтеграл та привести його до табличного інтегралу.

8. ;

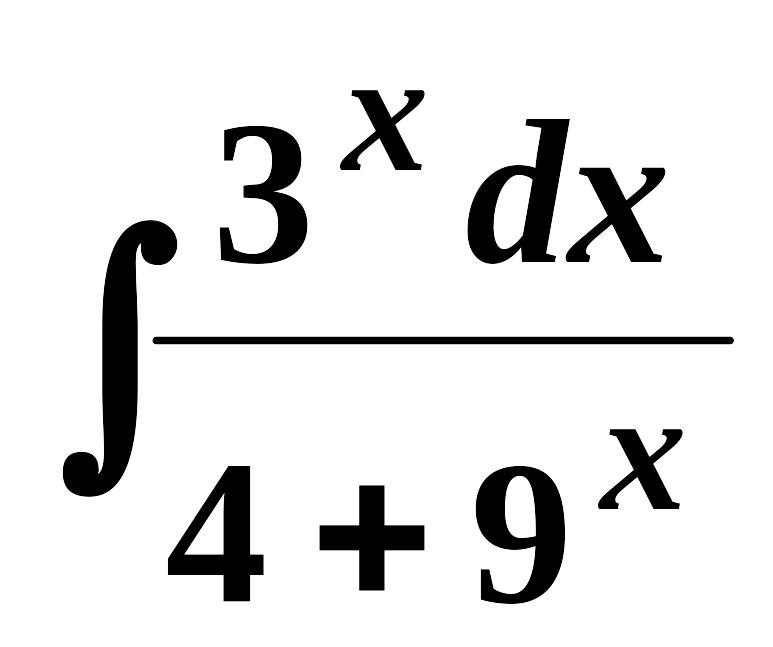9. ;

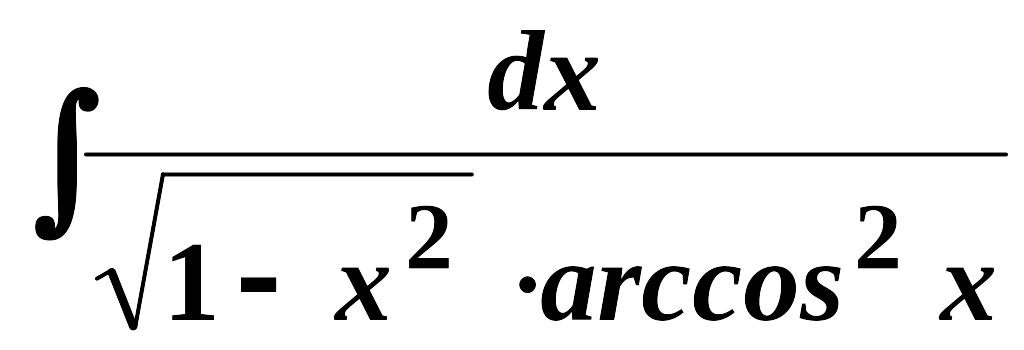10. ;

11. ;

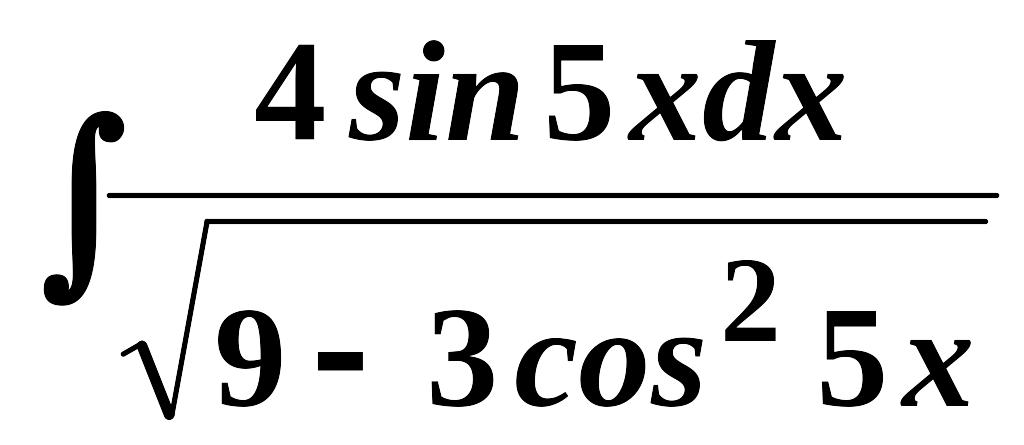12. .

3.3. Метод інтегрування частинами

Якщо та - функції, що мають на деякому проміжку неперервні похідні, то справедлива формула інтегрування частинами:

.

Тут вважається заданою ліва частина формули, тобто . Обчислення цього інтеграла зводиться до знаходження диференціала функції та функції за відомим її диференціалом . Функція визначається неоднозначно, з точністю до довільної сталої , тому вибирають ту функцію, яка має найпростіший вигляд (як правило, покладають ).

Методом інтегрування частинами зручно обчислювати такі типи інтегралів:

1) інтеграли виду , , , , де - многочлен -ого степеня від , - дійсне число . У цих інтегралах за слід взяти множник , а за - вираз, що залишився;

2) інтеграли виду , , , , . У цих інтегралах слід взяти за множник , , , , , а за - ;

3) інтеграли виду , , де - дійсні числа.

Тут після двократного застосування формули інтегрування частинами утворюється лінійне рівняння відносно шуканого інтеграла. Розв’язуючи це рівняння, знаходять інтеграл.

3.4. Інтегрування раціональних функцій

До раціональних функцій належать цілі та дробові раціональні функції. Інтегрування цілих раціональних функцій (многочленів) не складне. Розглянемо дробово-раціональну функцію (раціональний дріб), яка являє собою відношення двох многочленів степенів і із коефіцієнтами та відповідно:

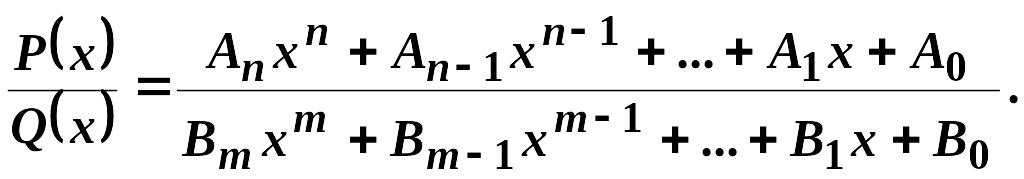(3.1)

Раціональний дріб називають правильним, якщо степінь чисельника менше від степеня знаменника < . У противному разі, а саме при , дріб називають неправильним.

Якщо раціональний дріб (3.1) неправильний, то діленням многочлена на його можна подати у вигляді суми цілої раціональної функції та правильного раціонального дробу, тобто

,

де многочлен - частка від ділення, многочлен - остача від ділення.

Отже, щоб проінтегрувати правильний раціональний дріб , треба:

1) розкласти многочлен на лінійні множники, які відповідають його дійсним кореням, та квадратні множники, які відповідають його комплексним кореням, а саме , де - дійсні числа, - цілі додатні числа, - -кратний дійсний корень многочлена , а квадратний тричлен не має дійсних коренів < ;

2) розкласти дріб на елементарні дроби таким чином:

(3.2)

,

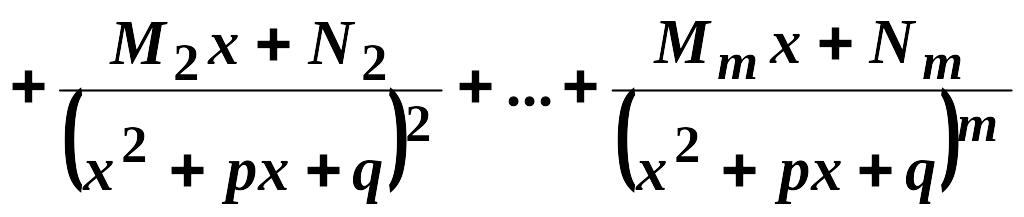де - невизначені коефіцієнти (деякі дійсні числа).

Для їх знаходження найчастіше користуються так званим методом невизначених коефіцієнтів. Потрібно звести праву частину рівності (3.2) до спільного знаменника, який дорівнює многочлену . В результаті дістанемо два рівні дроби з однаковими знаменниками, а їх чисельниками є тотожні многочлени. Порівнюючи далі коефіцієнти при однакових степенях лівої та правої частин тотожності, дістанемо систему лінійних алгебраїчних рівнянь, з якої визначаються шукані невідомі ,…,

.

Існує ще один спосіб знаходження невизначених коефіцієнтів. У рівності тотожніх многочленів чисельників лівого та правого дробу розкладання (3.2) слід надавати змінній довільні числові значення стільки разів, скільки коефіцієнтів потрібно визначити. При цьому обчислення значно спрощуються, якщо замість змінної брати значення коренів лінійних множників ;

3) тепер залишається обчислити як суму інтегралів від знайдених елементарних дробів. При цьому матимемо справу із наступними інтегралами:

I. , .

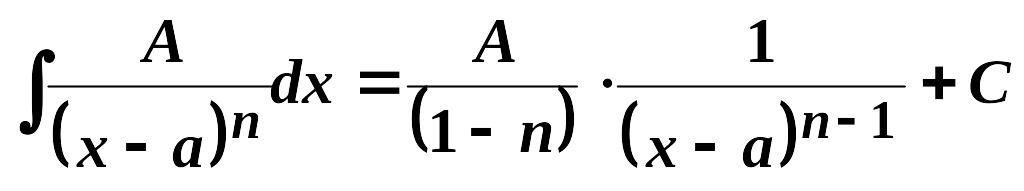II. , .

III. , .

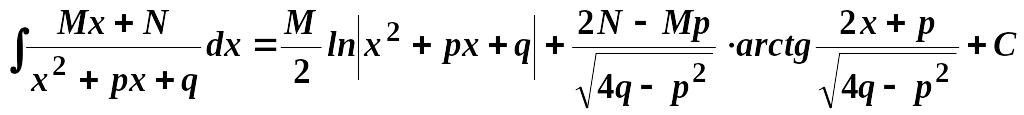IV. ,

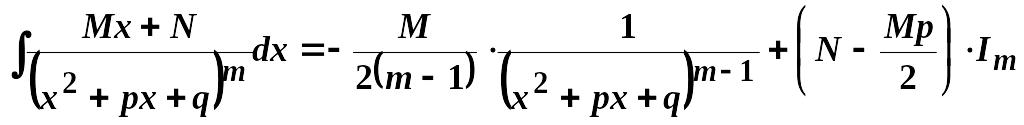де , , 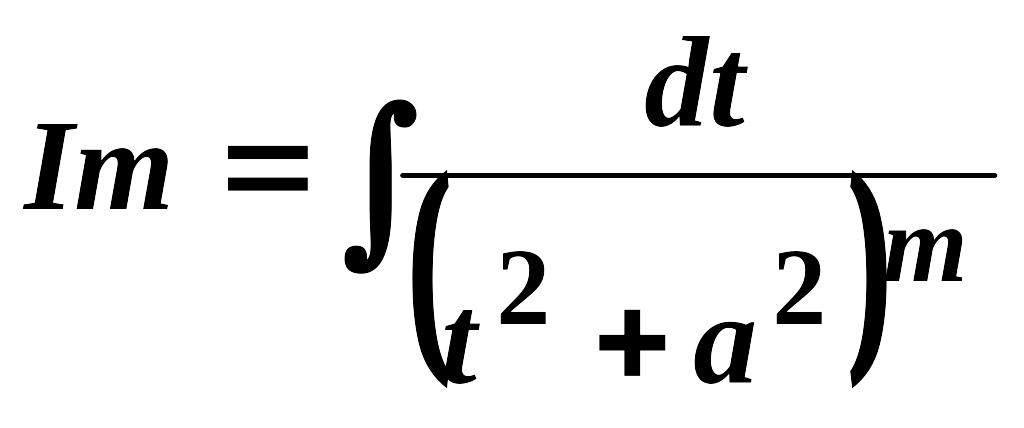в якому 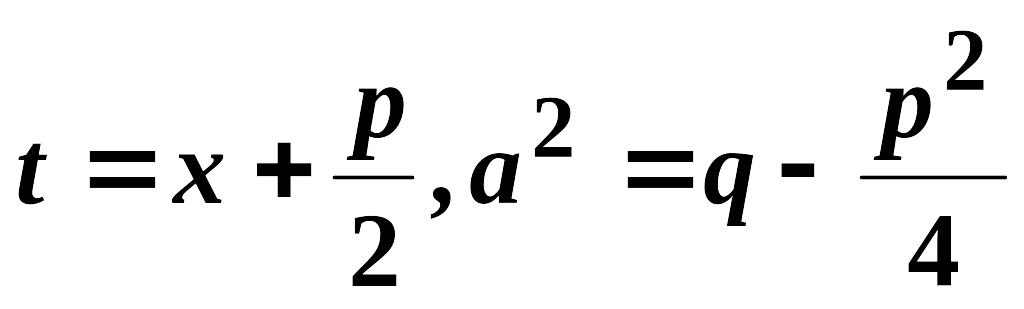, визначається - кратним застосуванням рекурентної формули

.
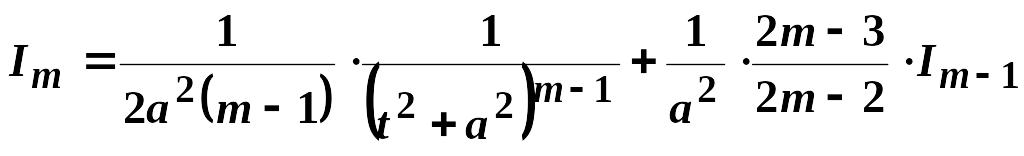