2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
Якщо задано функцію і обчислені її частинні похідні і , то вони також є функціями незалежних змінних і , а тому від кожної із них можна обчислити похідні як по змінній так і по змінній .
Частинні похідні від частинних похідних першого порядку називаються частинними похідними другого порядку. Вони позначаються:
,
,
,
.
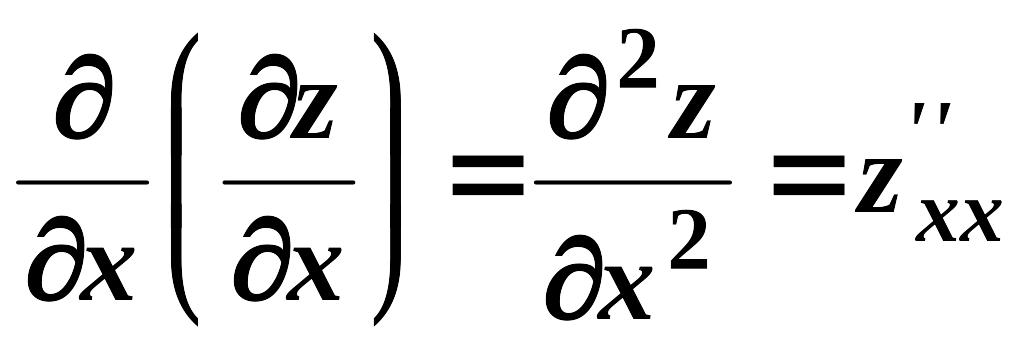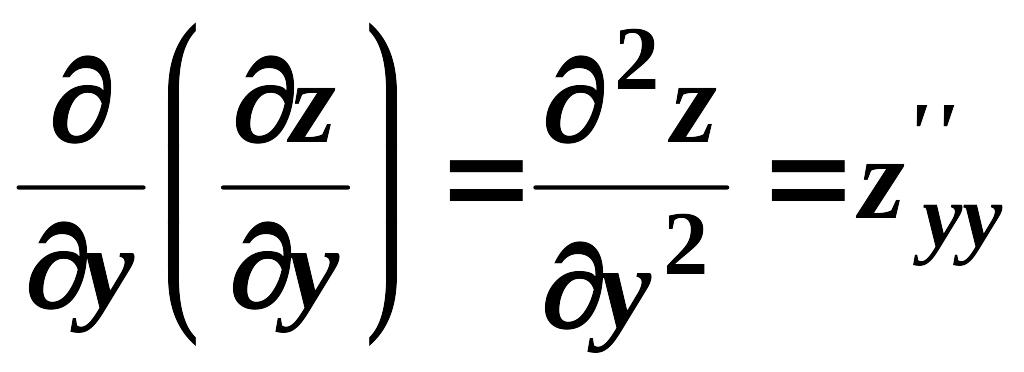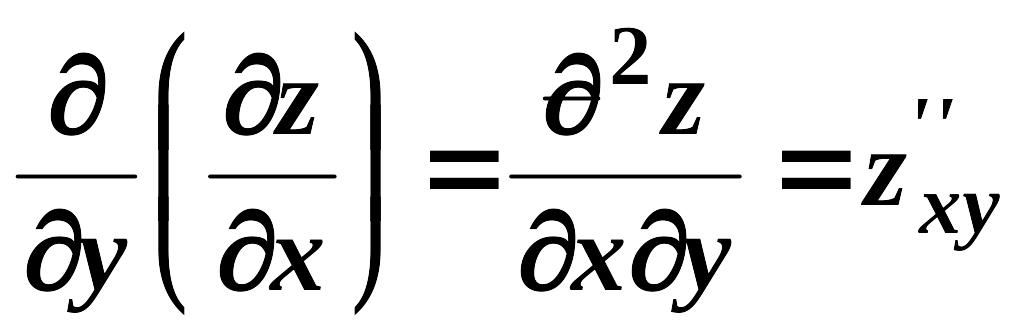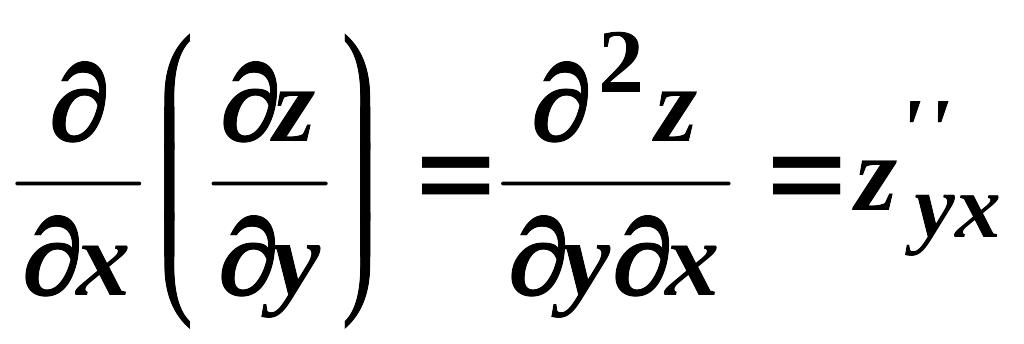Аналогічно означаються і позначаються частинні похідні вищих порядків.
Частинні
похідні, які відмінні одна від одної
лише порядком диференціювання,
називаються мішаними
похідними.
Вони є рівними між собою при умові їх
неперервності, тобто
.
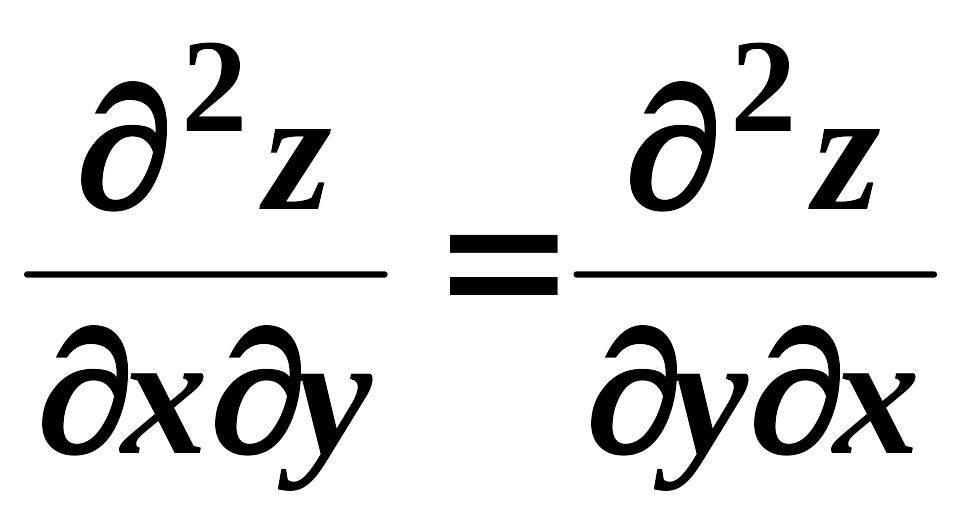Похідна
від неявної функції,
яку задано рівнянням
може бути обчислена за формулою:
.
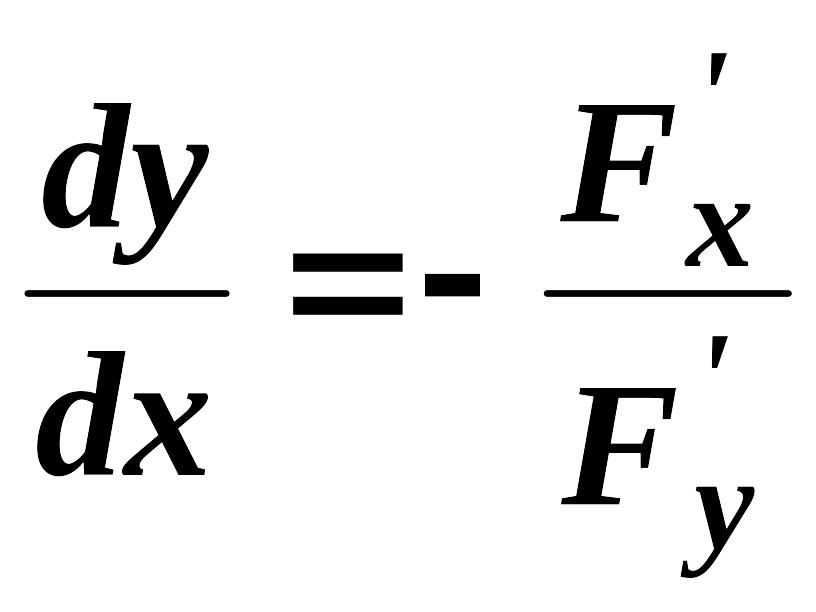(2.7)
Частинні
похідні неявної функції
,
заданої рівнянням
,
можуть бути обчисленні за формулами:
,
.
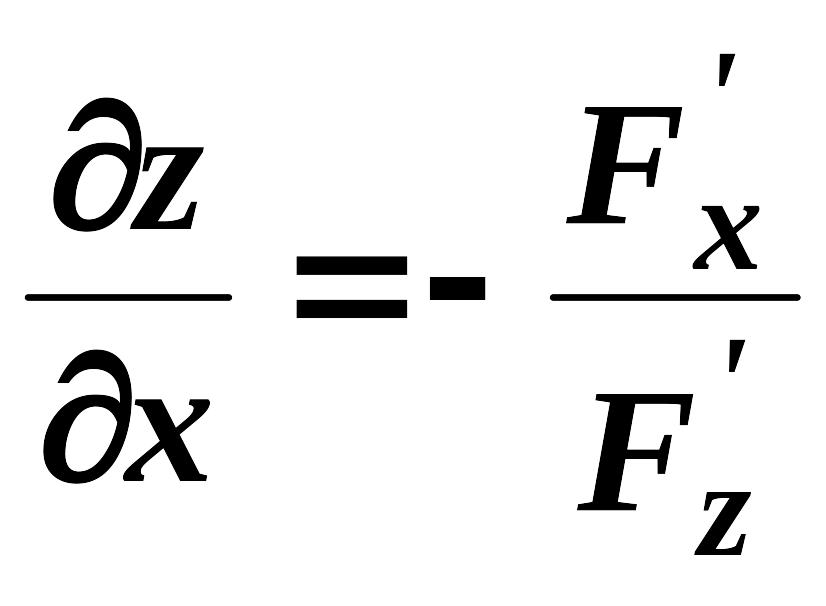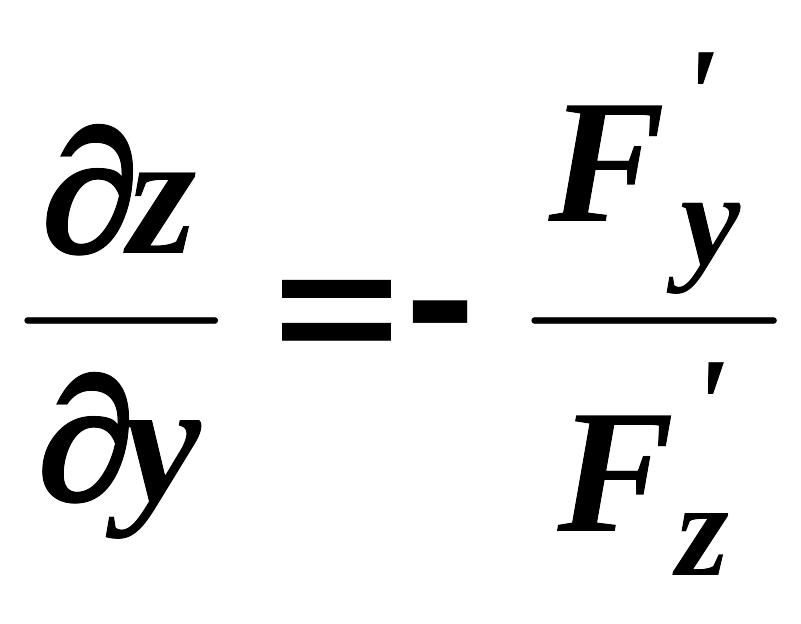(2.8)
2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
Рівняння
дотичної площини і нормалі до поверхні
в даній її точці
мають вигляд:
;
(2.9)
.
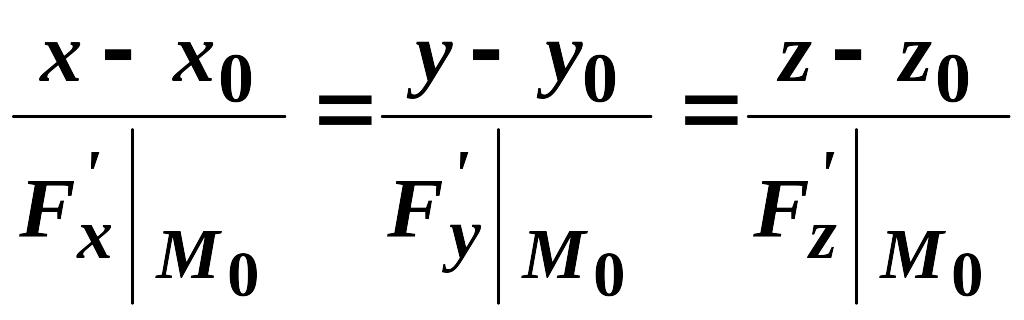(2.10)
Нехай
функція
визначена в деякому околі точки
.
Точка
називається точкою
максимуму (мінімуму) функції
,
якщо знайдеться такій окіл точки
,
в якому для будь-якої точки
виконується нерівність:
.
Максимуми і мінімуми функції називаються
її екстремумами,
а точки, в яких досягаються екстремуми
- точками
екстремуму.
Необхідна умова існування екстремуму.
Якщо диференційована функція має в точці екстремум, то в цій точці виконуються рівності:
,
.
(2.11)
Точки, в яких виконуються рівності (2.11), називаються точками можливого екстремуму або стаціонарними.
Достатня умова існування екстремуму функції.
Нехай
у точці
можливого екстремуму і деякому її околі
функція
має неперервні частинні похідні другого
порядку. Позначимо
і покладемо
.
Тоді:
а)
якщо
,
то
- точка екстремуму, причому при
- точка максимуму, при
- мінімуму;
б)
якщо
,
то в точці
екстремуму немає;
в)
у випадку
,
функція
у стаціонарній точці
може мати екстремум або ні.
Розділ 3 невизначений інтеграл
3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
Функція
називається первісною
функції
на проміжку
,
якщо
диференційовна на
і
для всіх
.
Очевидно, що будь-яка з функцій
,
де
- довільна стала, також є первісною
функції
на цьому проміжку.
Сукупність усіх первісних функції на проміжку називають невизначеним інтегралом функції на цьому проміжку і позначають
,
де
- підінтегральна функція,
- підінтегральний вираз,
- довільна стала.
Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.
Властивості невизначеного інтеграла:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
Якщо
і
- довільна функція, що має неперервну
похідну, то
.
При обчисленні невизначених інтегралів зручно користуватися наступними правилами: якщо , тоді
,
,
,
де
та
- сталі величини.
Таблиця основних інтегралів
1.
,
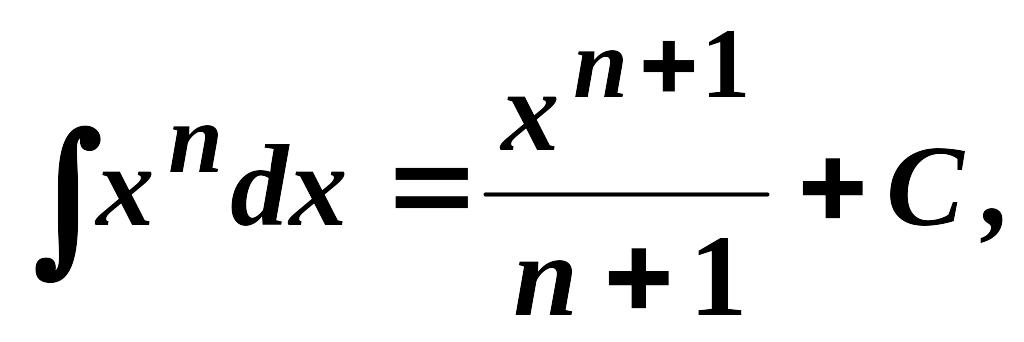
1'.
,
2.
,
3.
,
>
,
,
3'.
,
4.
,
5.
,
6.
,
7.
,
8.
,
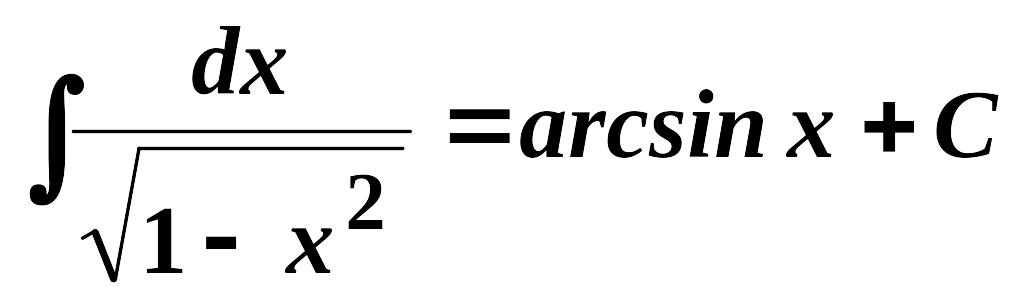8'.
,
>
,
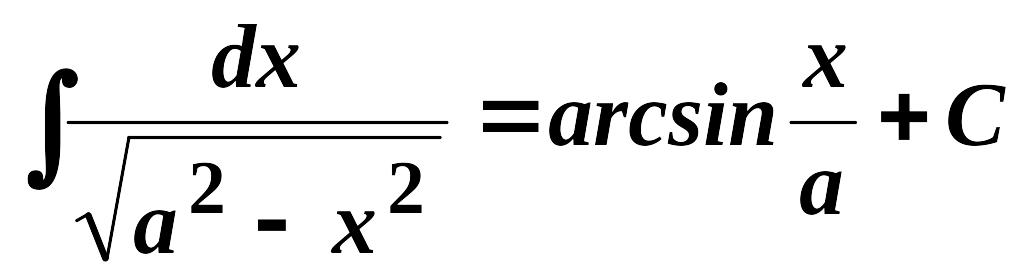9.
,
9'.
,
,
10.
,
,
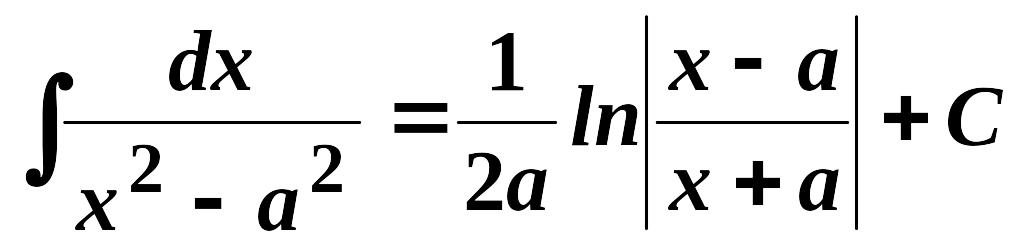11.
,
,
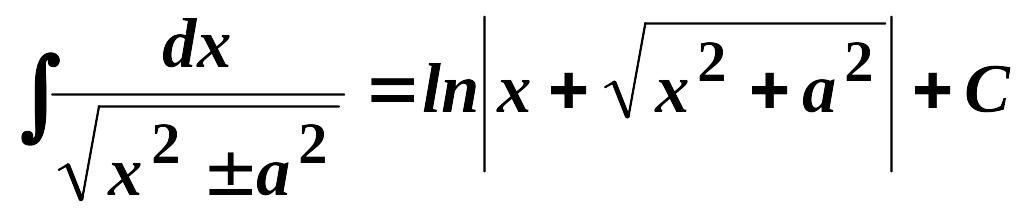12.
,
13.
,
14.
,
15.
.
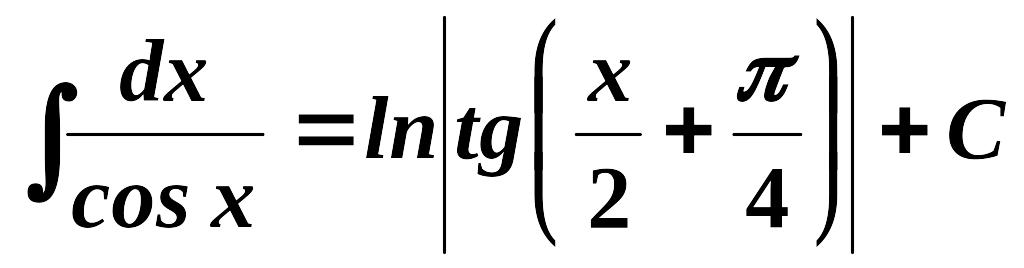Зауваження. Варто відзначити, що задача інтегрування функції вирішується неоднозначно. Тобто один і той же інтеграл може бути обчислений не єдиним методом.
Метод безпосереднього інтегрування полягає у зображенні вихідного інтеграла у вигляді алгебраїчної суми табличних інтегралів.