
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
имени ВЛАДИМИРА ДАЛЯ
Методические указания
к практическим занятиям
по дисциплине “Исследование операций в транспортных системах”
(для студентов специальностей “Организация перевозок и управление на транспорте”, “Транспортные системы”)
Часть 2 Модуль 1
УТВЕРЖДЕНО
на заседании кафедры
“Транспортные технологии”
протокол № _ от ________ г.
Луганск 2008
УДК 658
Методические указания к практическим занятиям по дисциплине “Исследование операций в транспортных системах” (для студентов специальностей “Организация перевозок и управление на транспорте”, “Транспортные системы”) / Сост.: О.М. Балицкая, Е.И. Кичкина, – Луганск: Изд-во Восточноукр. нац. ун-та им. В. Даля, 2008. – 20 с.
Методические указания предназначены в помощь студентам, обучающимся по направлению «Транспортные технологии» при выполнении практических заданий по дисциплине «Введение в исследование операций в транспортных системах» (первый модуль). Указания содержат методы решения задач, примеры решений отдельных задач, список литературы. Данные методические указания рекомендуются для студентов дневной и заочной форм обучения при проведении практических занятий.
Составители: О.М. Балицкая, асс.
Е.И. Кичкина, доц.
Отв. за выпуск
Рецензент:
Общие сведения
На практических занятиях первого модуля рассматриваются следующие задачи: задача линейного программирования, расширенная задача линейного программирования, двойственная задача и задача параметрического программирования. При выполнении практических заданий студент приобретает навыки формализации процесса, построения экономико-математической модели, решения задач линейного программирования, а также анализа устойчивости модели.
ЗАДАЧА 1
Построить модель по заданным условиям. С помощью геометрического метода найти решение задачи, состоящей в определении максимального значения функции
![]() (1.1)
(1.1)
при условиях
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
Методические указания к решению задачи
Каждое из неравенств (1.2), (1.3) системы
ограничений задачи геометрически
определяет полуплоскость соответственно
с граничными прямыми
![]() ,
X1=0 и
Х2=0. В том случае, если система
неравенств (1.2), (1.3) совместна, область
ее решений есть множество точек,
принадлежащих всем указанным
полуплоскостям. Так как множество точек
пересечения данных полуплоскостей —
выпуклое, то областью допустимых решений
задачи является выпуклое множество,
которое называется многоугольником
решений. Стороны этого многоугольника
лежат на прямых, уравнения которых
получаются из исходной системы ограничений
заменой знаков неравенств на знаки
точных равенств.
,
X1=0 и
Х2=0. В том случае, если система
неравенств (1.2), (1.3) совместна, область
ее решений есть множество точек,
принадлежащих всем указанным
полуплоскостям. Так как множество точек
пересечения данных полуплоскостей —
выпуклое, то областью допустимых решений
задачи является выпуклое множество,
которое называется многоугольником
решений. Стороны этого многоугольника
лежат на прямых, уравнения которых
получаются из исходной системы ограничений
заменой знаков неравенств на знаки
точных равенств.
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст, и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.
Алгоритм решения задачи линейного программирования на основе ее геометрической интерпретации:
Построение прямых, соответствующих уравнениям, которые получены в результате замены в неравенствах-ограничениях знаков неравенств на знаки точных равенств.
Нахождение полуплоскостей, определяемых каждым из ограничений задачи.
Определение многоугольника решений (области допустимых решений ОДР).
Построение вектора-градиента по коэффициентам функции цели
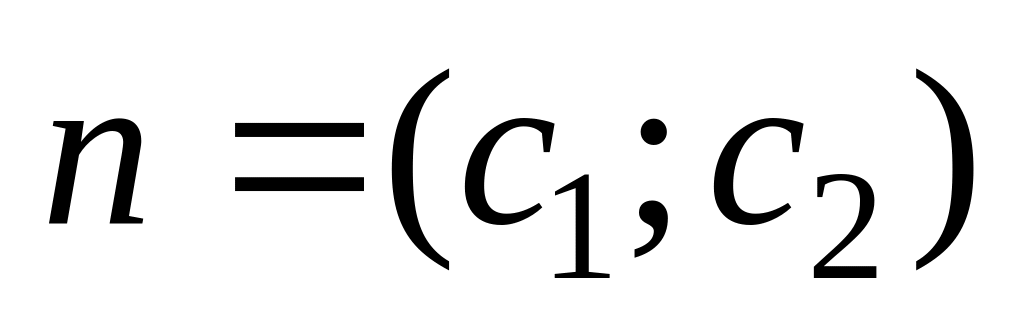 .
.Построение прямой функции цели, перпендикулярную вектору-градиенту и проходящую через многоугольник решений.
Передвижение прямой функции цели в направлении вектора-градиента, в результате чего находят либо решение задачи, либо устанавливают неограниченность сверху на множестве решений.
Определение точки, соответствующей решению задачи и значения функции цели в ней.
При построении многоугольника решений (области допустимых решений) могут встретиться следующие варианты:
Область допустимых решений пустая, если система ограничений несовместна (рис. 1.1);
Область допустимых решений может быть в виде одной точки (рис. 1.2);
Область допустимых решений является выпуклым многогранником (рис 1.3);
Область допустимых решений является неограниченной выпуклой многогранной областью (рис 1.4).

Рис. 1.1 Область допустимых решений пустая
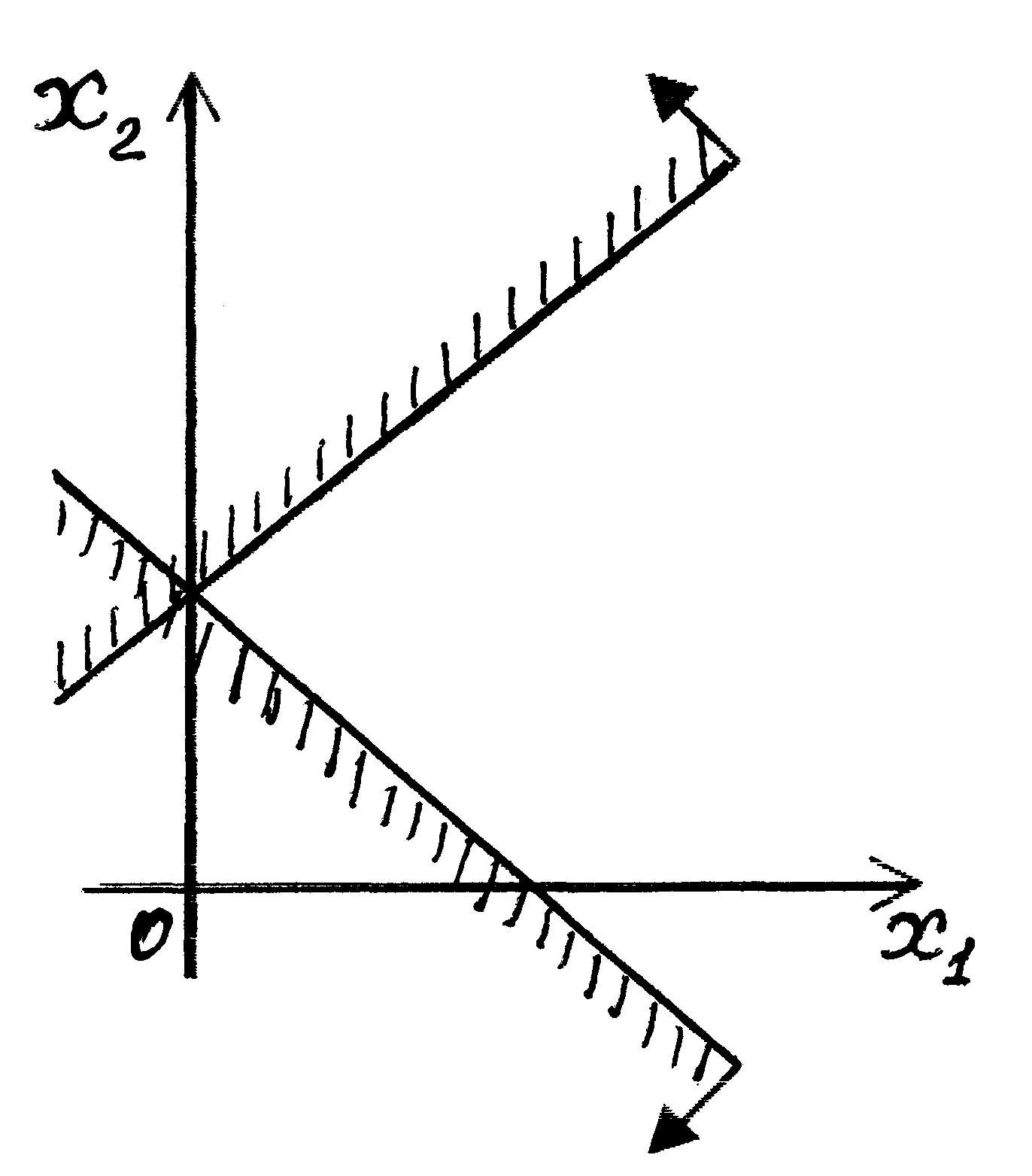
Рис.1.1
Рис.1.2 Область допустимых решений может быть в виде одной точки

Рис.1.3 Область допустимых решений является выпуклым многогранником

Рис.1.4 Область допустимых решений является неограниченной выпуклой многогранной областью
Для задач, область допустимых решений которых представляет собой выпуклую многогранную область, возможны два варианта:
Максимум целевой функции достигается в одной точке (рис 1.5);
Максимальное значение целевой функции имеет место в двух вершинах А и В и, следовательно, в любой точке отрезка АВ (рис. 1.6).
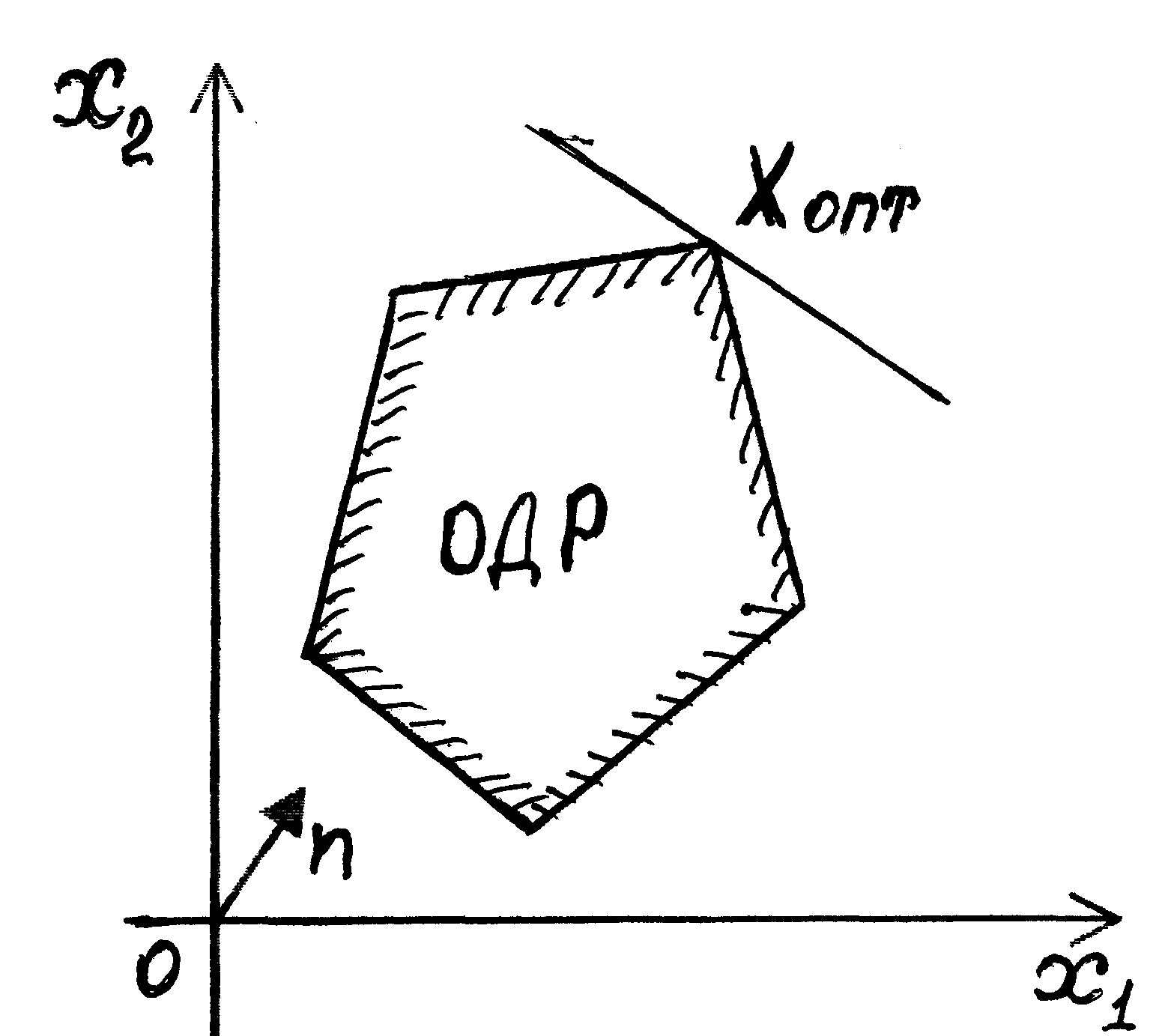
Рис. 1.5 Максимум целевой функции достигается в одной точке

Рис. 1.6 Максимальное значение функции – отрезок.
В случае, когда область допустимых решений неограниченна, могут встретиться следующие варианты:
Целевая функция имеет экстремум (рис.1.7);
Функция ограничена сверху и снизу, т.е.

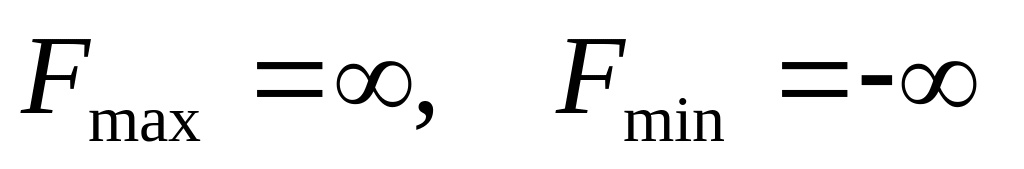 (рис.1.8).
(рис.1.8).

Рис. 1.7 Целевая функция имеет экстремум
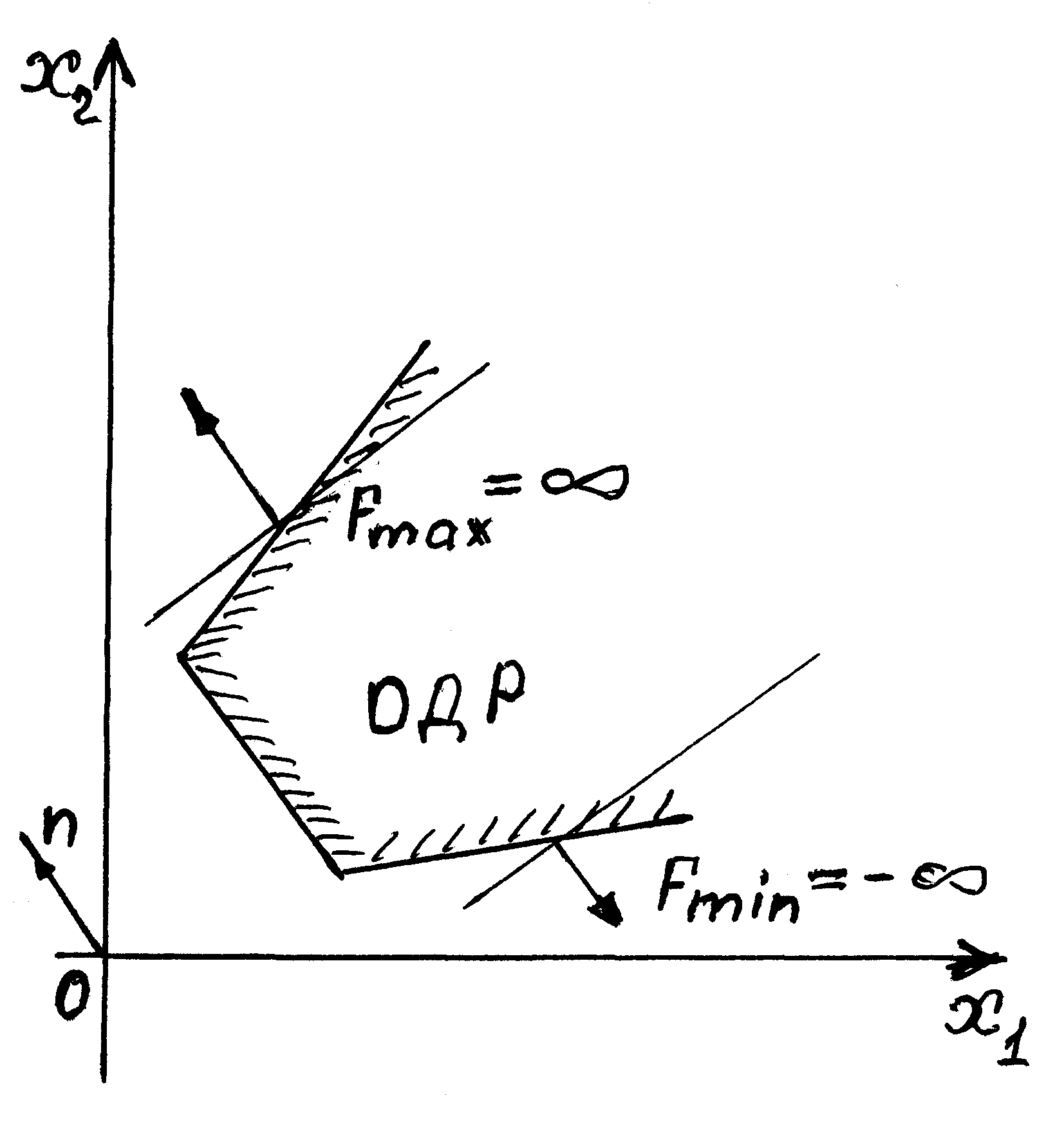
Рис. 1.8 Функция ограничена сверху и снизу
