§ 1.2. Опыты Резерфорда. Ядерная модель атома

1. В опытах Резерфорда использовались потоки заряжен-ных частиц, так называемые –лучи, которые испускаются радио-активными веществами, например, радием или радоном. Как впер-вые доказали Резерфорд и Ройдс (1909), –лучи представляют со-бой пучок двукратно ионизованных атомов гелия. Благодаря своей большой энергии (несколько МэВ) и большой массе альфа–час-тицы создавали макроскопически наблюдаемые эффекты при рас-сеянии атомами вещества. Необходимость использования радио-активных препаратов, как источников частиц больших энергий, отпала после создания в 30-х годах 20-го столетия ускорителей заряженных частиц. Существенно усовершенствованы с тех пор также методы детектирования заряженных частиц.

До Резерфорда счита-лось, что рассеяние частиц на большие углы при их прохож-дении сквозь тонкую пластин-ку вещества является резуль-татом большого числа актов малого рассеяния отдельными

Рис.1.1 атомами. Однако опыты, кото-

рые проводили под руковод-ством Резерфорда Гейгер и Марсден (1909), показали, что неко-торые из частиц уже при отдельных столкновениях испытывают отклоне-ния на большие углы, превышающие . Например, при столкновении с фольгой из платины примерно одна из 8000 альфа–частиц отражалась назад. Это согласовывалось с расчетами, ко-торые показали, что вероятность от-клонения альфа–частицы на и больше очень мала. Вероятность пос-ледующего столкновения с таким же большим отклонением и в ту же сто-

Рис.1.2 рону вообще должна быть ничтожной.

Поэтому, чтобы произошло большое отклонение частицы при однократном столкновении, естественно было предположить, что в атоме имеется сильное электрическое поле (с напряженностью порядка В/см). Так Резерфорд пришел к ядерной модели атома. Согласно этой модели положительный

заряд атома сосредоточен в его центре в небольшой области с размерами порядка см. Тогда становятся понятными ре-зультаты опытов: большинство –частиц проходит вдали от ядра и поэтому направление их движения меняется слабо. Немногие же частицы, которые близко подходят к ядру, испытывают сильное отталкивание и отклоняются на большие углы (рис.1.1). Такая картина (рис.1.2) отчетливо наблюдается на снимках треков (следов) –частиц в камере Вильсона (1912).

2. На основе ядерной модели Резерфорд разработал теорию рассеяния альфа–частиц атомами вещества. Было показано, что для всех отклонений, превышающих один градус, можно рас-сматривать взаимодействие альфа–частиц только с полем ядра и пренебрегать их взаимодействием с электронами. Это обусловлено как малым отношением массы электрона к массе альфа–частиц (1/7360), так и их большой энергией. Рассматривая взаимодействие –частицы с ядром некоторого атома, можно пренебречь ее взаи-модействием с ядрами других атомов, поскольку они находятся достаточно далеко друг от друга. Таким образом, возникает упро-щенная задача двух тел с центральным взаимодействием. Это взаимодействие, по предположению, описывается кулоновской силой отталкивания между ядром и –частицей.

Рис.1.3

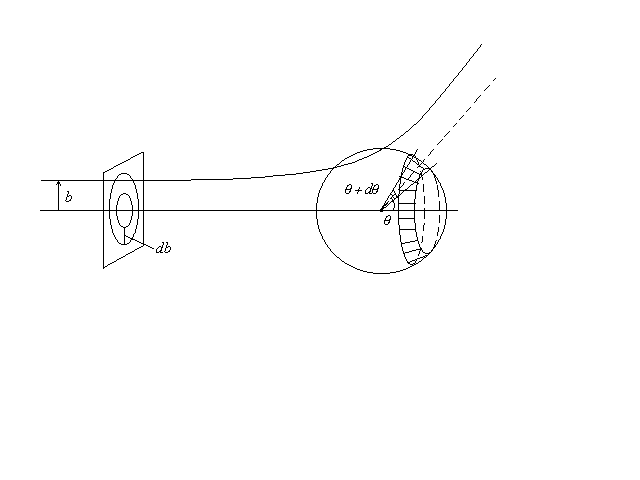
Такая задача аналогична известной из курса механики задаче Кеплера о движении частицы в поле силы тяготения. Если масса ядра намного превышает массу –частицы, то движением ядра можно пренебречь. Чтобы учесть движение ядра, достаточно в ре-шении задачи заменить массу –частицы на приведенную массу. Траекторией –частицы является гипербола, вид которой зависит от прицельного параметра b (рис.1.3). Угол рассеяния и при-цельный параметр связаны формулой (см. задачи):

. (1.2)

Здесь M – масса альфа–частицы, – ее скорость на бесконечно большом удалении от ядра, Ze – заряд ядра. Число Z, как это впер-вые доказал ученик Резерфорда Мозли (1913) из анализа рентге-новских спектров атомов, равно порядковому номеру атома в пе-риодической системе элементов Д.И. Менделеева. Заряд альфа–частицы равен 2e.

Рассеяние частиц характеризуется дифференциальным се-чением , имеющим размерность площади. По определению,

, (1.3)

где – число частиц, рассеянных в единицу времени в элемент телесного угла (рис.1.3), – плотность потока падающих частиц, т.е. число частиц на единице площади, перпендикулярной направлению их движения, сталкивающихся с рассеивающим цен-тром в единицу времени. Углам рассеяния в интервале cоответствуют изменения прицельного параметра в интервале от b до b+db.

Картина рассеяния не зависит от азимутального угла. Она является симметричной в плоскости, перпендикулярной плоскости рисунка. В этой плоскости изменению прицельного параметра от b до b+db соответствует кольцо шириной db. Частицы, «метя-щие» в это кольцо как в «мишень», будут рассеиваться в области, характеризуемой углами рассеяния в интервале , . Таким образом, площадь кольца определяет дифференциальное сечение рассеяния:

. (1.4)

Переходя от прицельного параметра к углу рассеяния с помощью соотношения (1.2), получаем формулу Резерфорда:

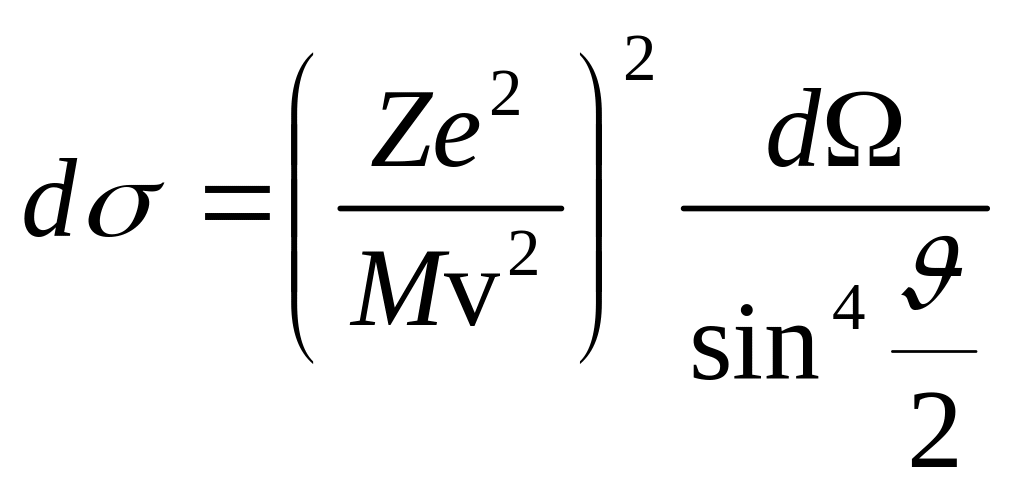, (1.5)

где d – элемент телесного угла. Формулой (1.5) объ-ясняются экспериментальные факты, которые привели Резерфорда к открытию ядерной модели атома. Из нее следует, например, что большее число –частиц рассеивается на малые углы. Вместе с тем, для очень малых углов рассеяния (меньше ) формула Резер-

форда не применима.

3. Формула Резерфорда непосредственно проверялась в эксперименте. Для обеспечения условия однократности соударе-ния –частицы с атомом в опытах использовались очень тонкие металлические пленки, так называемые фольги толщиной Формула (1.5) описывает рассеяние –частиц одним ядром. Если в рассеивающей фольге плотность ядер равна n, то их общее число равно nV, где V – объем фольги. Таким образом, чи-сло рассеянных –частиц в единицу времени определяется фор-мулой:

. (1.6)

Отсюда следует соотношение:

. (1.6a)

В условиях эксперимента все величины, входящие в правую часть формулы (1.6а), являются неизменными. Тогда произве-дение должно оставаться постоянным. Это и проверялось на опыте Гейгером и Марсденом (1913). Схема их установки изображена на рис.1.4.

В металлической цилиндрической камере В помещались: источник альфа–частиц R, рассеивающая фольга F и мик-роскоп М, на котором закреплен экран S из Рис 1.4

сульфида цинка. Камера укреплялась на

платформе А с делениями по образующей. Фольга и источник находились на трубке Т, которая закреплена в станине L. При повороте камеры на платформе А вокруг своей оси перемещался также микроскоп. С его помощью проводился подсчет рассеянных –частиц по числу вспышек (сцинтилляций) на экране. Опыты, проведенные на фольгах разной толщины и из разного материала, показали, что, несмотря на сильное различие числа рассеянных –частиц при разных углах рассеяния, произведение (1.6а), как видно из таблицы 1, в пределах погрешностей эксперимента оставалось постоянным. Тем самым формула Резерфорда была подтверждена экспериментально.

Однако при очень малых углах рассеяния (большие прицельные параметры) наблюдаются отклонения от формулы Резерфорда. Это связывают с эффектом экранировки кулоновского поля ядра атомными электронами.

Таблица 1

		Серебряная фольга		Золотая фольга
		dN1		dN1
150о	1.15	22.2	19.3	33.1	28.8
135о	1.38	27.4	19.8	43.0	31.2
120о	1.79	33.0	18.4	51.9	29.0
105о	2.53	47.3	18.7	69.5	27.5
75о	7.25	136	18.8	211	29.1
60о	16.0	320	20.0	477	29.8
45о	46.6	989	21.2	1435	30.8
37.5о	93.7	1760	18.8	3300	35.3
30о	223	5260	23.6	7800	35.0
22.5о	690	20300	29.4	27300	39.6
15о	3445	105400	30.6	132000	38.4

Расхождения опытных данных с формулой (1.6) наблюда-ются также, когда прицельный параметр становится меньше см (или при достаточно большой энергии –частиц). На таких расстояниях действуют ядерные силы, имеющие характер корот-кодействующих сил притяжения и не зависящие от заряда частиц. Можно оценить радиус действия ядерных сил (радиуса ядра атома) с помощью следующих соображений. При рассеянии альфа–частиц, например, свинцовой фольгой (Z=82) под углом 60^о отклонение от формулы Резерфорда наблюдается при энергии 27,5 МэВ. Минимальное расстояние, на которое приближается к ядру альфа–частица, может служить в этом случае мерой радиуса ядра. Минимальное расстояние сближения альфа–частицы с ядром опре-деляется формулой (см. задачи): . С помощью приведенных данных получаем: см.

Отклонения от теории Резерфорда наблюдались также при рассе-янии альфа–частиц по разным направлениям легкими элементами. В этом случае говорили об «аномальном» рассеянии α–частиц. Объясняли это так: поскольку заряд ядра тяжелых атомов довольно большой, то силы

отталкивания между ними и α–частицами очень велики. Эти силы зас-тавляют α–частицы отклоняться от своего пути еще сравнительно далеко от ядра. В случае легких элементов, заряд ядра которых сравнительно не-велик, силы отталкивания намного слабее, так что α–частицы могут близ-ко подходить к ядру, и, возможно, даже проникать в него. Такие рассуж-дения привели Резерфорда к мысли о возможности расщепления атомных ядер с помощью быстрых α–частиц. В качестве «снарядов», способных пробить «броню» обычных нерадиоактивных ядер, Резерфорд выбрал самые быстрые α–частицы, испускаемые радием С'. Они имеют скорость 19 200 км/с. Свои опыты, завершившиеся открытием расщепления ядра атома азота α–частицами, Резерфорд проводил в 1919 г. В этих опытах было открыто также ядро атома водорода, получившее впоследствии наз-вание «протон». Окончательное доказательство существования протона как составной части ядер всех атомов было проведено в опытах Блэккета (1925). Исследовав огромное количество треков альфа–частиц в камере Вильсона, Блэккет доказал также, что в упомянутых опытах Резерфорда происходило не разрушение ядра атома азота, а скорее превращение этого ядра: в результате проникновения в него α–частицы (ее символ ) азот ( ) превращается в кислород ( ), при этом испускается протон . Этот процесс изображается формулой: .

4 . Формула Резерфорда проверялась также другим мето-дом. Блэккет исследовал рассеяние –частиц в газах с помощью камеры Вильсона. Им было получено большое количество фото-графий треков –частиц в различных газах. По этим фотографиям измерялись углы отклонения –частиц и подсчитывалась частота появления определенных углов рассеяния. Такие измерения позво-лили изучить границы применимости закона Кулона (1785), лежа-щего в основе формулы Резерфорда. Оказалось, что закон Кулона справедлив, например, при рассеянии –частиц в аргоне в пре-делах расстояний между ядром и –частицей от до см, а в воздухе – в пределах от до см.

5. Формула (1.6) позволяет также непосредственно найти число Z, определяющее заряд ядра. Для этого надо фиксировать все вели-чины, кроме Тогда, измеряя Рис.1.5

на опыте число рассеянных альфа–час-

тиц и плотность потока падающих частиц, по формуле (1.6) можно

определить число Z. Трудность эксперимента состоит в том, что величины и J сильно отличаются друг от друга. Например, если в одну минуту рассеивается 30 альфа–частиц, то число пада-

ющих частиц в минуту равно 20000. Чтобы обойти эту трудность, английский физик Чэдвик (1920) создал установку, схема которой изображена на рис.1.5. Рассеивающая фольга в виде кольца распо-лагалась на одинаковом расстоянии от источника альфа–частиц R и флуоресцирующего экрана S. Для подсчета рассеянных –час-тиц отверстие кольца закрывалось свинцовым экраном. Для изме-рения J закрывалось экраном кольцо, а его отверстие оставалось свободным. Из опытов Чэдвика следовало: для меди Z = 29,3, для серебра Z = 46,3, для платины Z = 77,4. Порядковые номера этих элементов равны, соответственно, 29, 47, 78. Таким образом, был убедительно подтвержден уже известный в то время результат Мозли.

6. Справедливость формулы Резерфорда означает, что правильными являются основные предположения, при которых она получена. Напомним эти предположения:

1) атом имеет планетарное строение. В центре атома нахо-дится ядро с размерами порядка , в котором сосредо-точена большая часть массы атома. Число Z, определяющее заряд ядра, совпадает с порядковым номером атома в периодической системе элементов. Электроны атома обращаются вокруг ядра, как планеты вокруг Солнца;

2) закон Кулона описывает взаимодействие между точеч-ными зарядами также и на атомных расстояниях.

7. Ядерная модель Резерфорда явилась крупной вехой в развитии представлений о строении атома. Вместе с тем эта мо-дель содержит в себе принципиальные недостатки:

1) ни эксперименты, ни теория Резерфорда не дают оценок размеров атома (напомним, что атом имеет размеры порядка ). Это связано с тем, что из фундаментальных физи-ческих постоянных, определяющих планетарную модель атома – (масса ядра), нельзя составить величину с размерностью длины. Поэтому неясно, например, почему все атомы данного эле-мента должны иметь одинаковый размер; кроме того, поскольку движение в центральном поле сил является плоским, то атомы водорода должны были бы быть плоскими;

2) самое главное, планетарная модель противоречит само-му факту существования атома. Дело в том, что обращающиеся вокруг ядра согласно планетарной модели электроны движутся не-

равномерно. А из классической электродинамики известно, что не-равномерно движущийся заряд должен излучать электромагнит-ные волны. Это должно приводить к непрерывной потере энергии

электроном и, в результате, – к непрерывному уменьшению ради-уса его обращения вокруг ядра. Так что траекторией электрона должна быть не замкнутая кривая (окружность или эллипс), а скручивающаяся спираль, оканчивающаяся «падением» электрона на ядро. Это должно происходить за чрезвычайно малое время – порядка с (см. задачи);

3) по представлениям классической физики частота линии излучения, испускаемого атомом, определяется частотой обраще-ния электрона вокруг ядра и ее гармониками, так что спектр излу-чения должен бы представлять собой набор равноотстоящих ли-ний (если забыть про «падение» электрона на ядро). Это противо-речит экспериментальным фактам, которые показывают, что опти-ческий спектр излучения атомов состоит из сгущающихся дис-кретных линий. Таким образом, если пользоваться представлени-ями классической физики, то планетарная модель атома не объяс-няет ни факта существования устойчивых атомов, ни спектраль-ных закономерностей их излучения.

8. В атомной физике удобной единицей энергии является эле-ктрон-вольт (эВ). Единица энергии 1 эВ – это энергия, которую приоб-ретает электрон, проходя ускоряющую разность потенциалов в 1 В. Так как , то 1 эВ = эрг = эрг. Скорость электрона см/c.

ЗАДАЧИ

1. Оценить классический радиус электрона, считая, что его электроста-тическая энергия равна энергии покоя.

Р е ш е н и е. .

2. Вывести формулу (1.2).

Р е ш е н и е. Используем законы сохранения энергии и момента им-пульса: Переходя от произ-водной по времени к производной по , для переменной , полу-чаем уравнение: Отсюда: При , , т.е. Это дает Величина при равна прицельному параметру. Таким образом, В=1/b, так что . Учитывая, что после отклонения альфа–частицы , получаем (1.2).

3. Найти минимальное расстояние между альфа-частицей и ядром.

Р е ш е н и е. Из законов сохранения энергии и момента импульса имеем:

. Из этих уравнений получаем: .

4. Найти зависимость минимального расстояния от угла рассеяния.

О т в е т. .

5. Определить величину импульса отдачи, приобретаемого ядром при рассеянии альфа-частицы.

О т в е т.

6. Оценить величину напряженности электрического поля в атоме.

Р е ш е н и е. .

7. Оценить время «падения» электрона на ядро в планетарной модели атома водорода вследствие потерь энергии электроном на излучение (радиус атома водорода

Р е ш е н и е. Потери энергии электроном, движущимся с ускорением , определяются формулой . Приближенно можно считать траекторию электрона окружностью. Поэтому . С другой сто-роны, при вращении электрона вокруг ядра энергия электрона равна . Таким образом, получаем уравнение

. Отсюда . В момент падения . Следовательно