
- •Разложение периодической функции в ряд Фурье
- •Ряды Фурье для четных и нечетных функций.
- •Ряд Фурье в комплексной форме.
- •Спектральные характеристики ряда Фурье.
- •Спектральные характеристики для вещественной формы.
- •Спектральные характеристики для комплексной формы.
- •Спектральная функция.
- •Нахождение сумм числовых рядов.
- •Разложение непериодической функции.
- •Интеграл Фурье в вещественной форме.
- •Интеграл Фурье для четной и нечетной функций.
- •Спектральные характеристики интеграла Фурье.
Спектральные характеристики для комплексной формы.
Частотные спектры: представляют собой последовательность частот и частот
 где
где
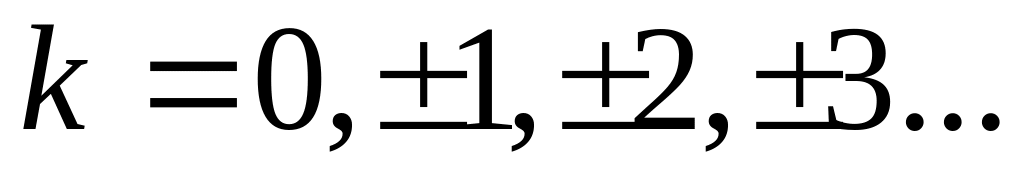 в зависимости от
.
Эти спектры симметричны относительно
начала координат (так как
в зависимости от
.
Эти спектры симметричны относительно
начала координат (так как
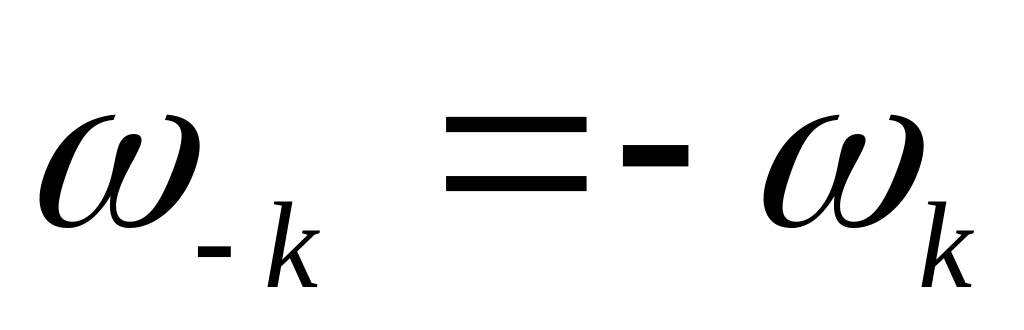 и
и
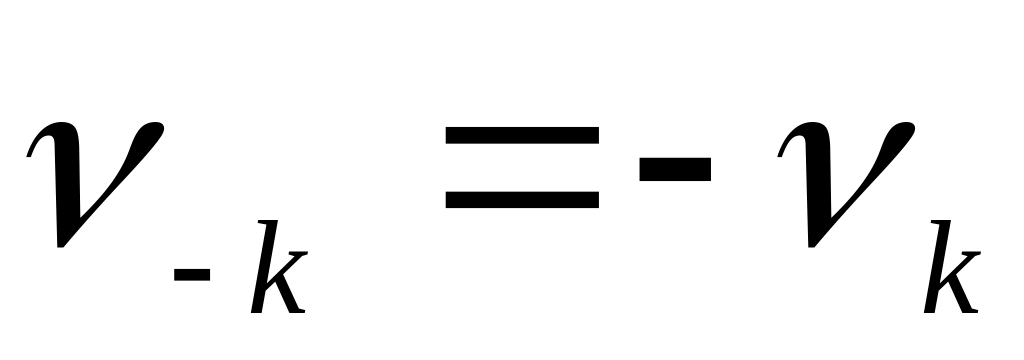 при
при
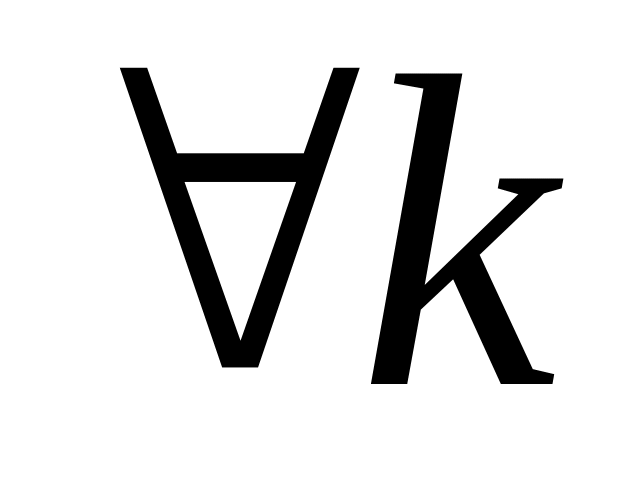 ).
).
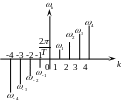
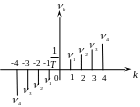 2. Линейчатые
спектры: представляют собой
последовательность
2. Линейчатые
спектры: представляют собой
последовательность
![]()
![]() ,
где
,
где
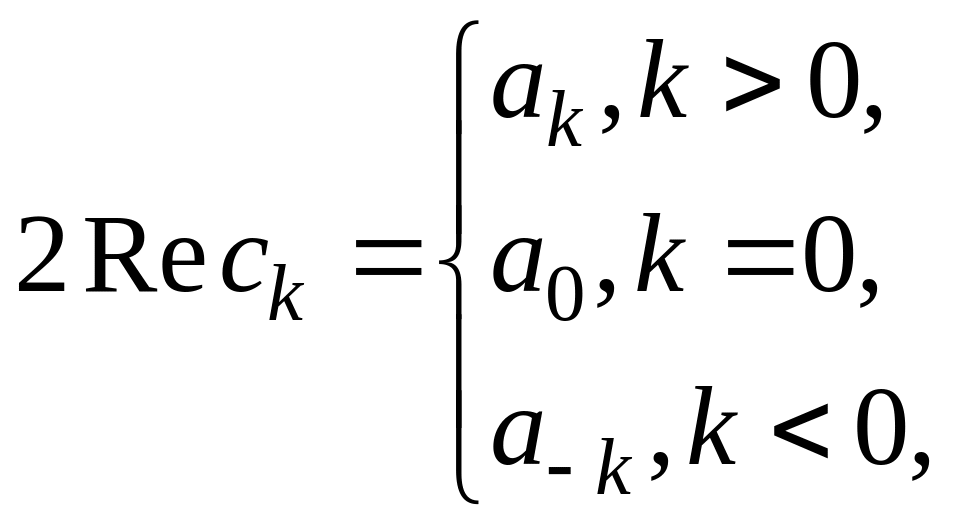 и последовательность
и последовательность
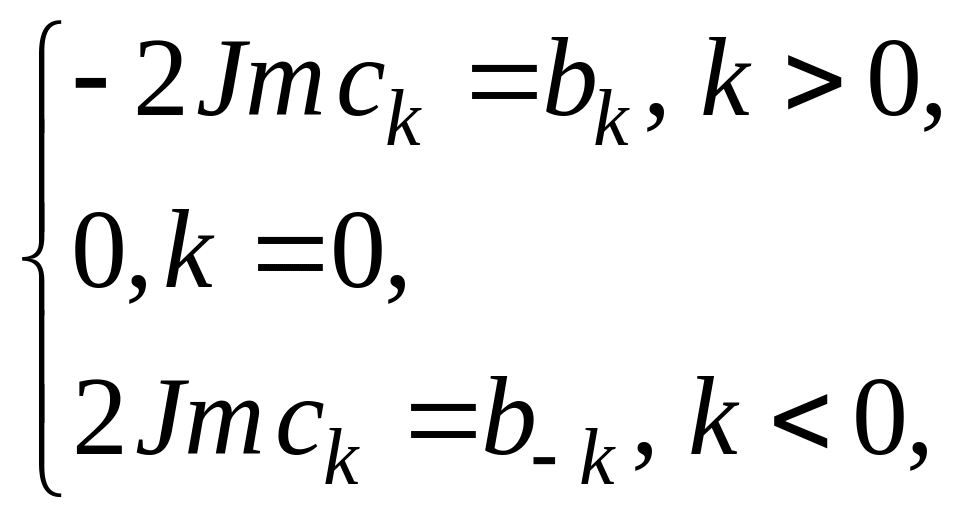 где
,
в зависимости от
.
где
,
в зависимости от
.
Эти спектры
симметричны относительно оси ординат
(т.к.
![]() и
и
![]() ).
).

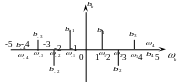 3. Амплитудный
спектр (амплитудно-частотный): представляет
собой последовательность
3. Амплитудный
спектр (амплитудно-частотный): представляет
собой последовательность
![]() ,
,
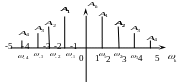
при
![]() и
и
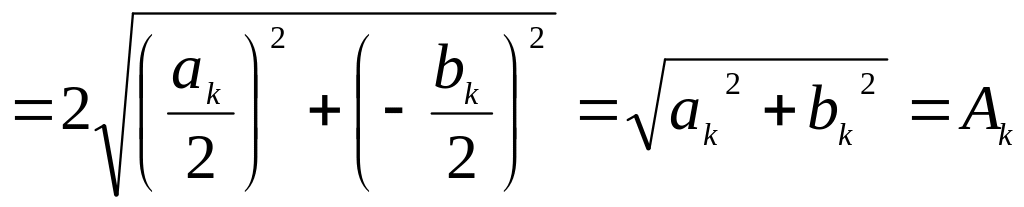
при
![]() и
и
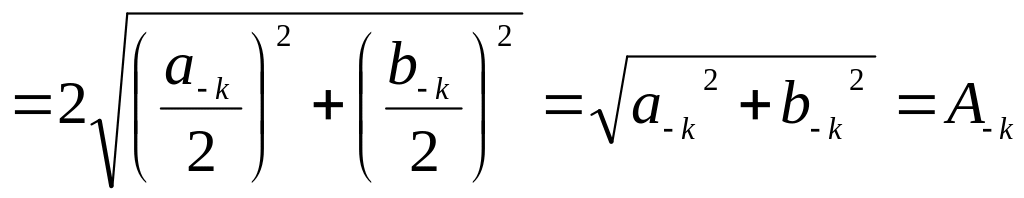
при
![]() и
и
![]()
Этот спектр
симметричен относительно оси ординат,
т.к.
=![]() .
.
4. Фазовый спектр
(фазово-частотный): представляет собой
последовательность
![]() при
в зависимости от
.
при
в зависимости от
.
Этот спектр
симметричен относительно начала
координат (так как
![]() и
и
![]() ).
).
Можно заметить, что спектральные характеристики для комплексной формы при совпадают со спектральными характеристиками для вещественной формы.
Спектральная функция.
В комплексной записи ряда Фурье перейдем к частоте , измеряемой в герцах: .
Используя соотношение
![]() ,
получим:
,
получим:
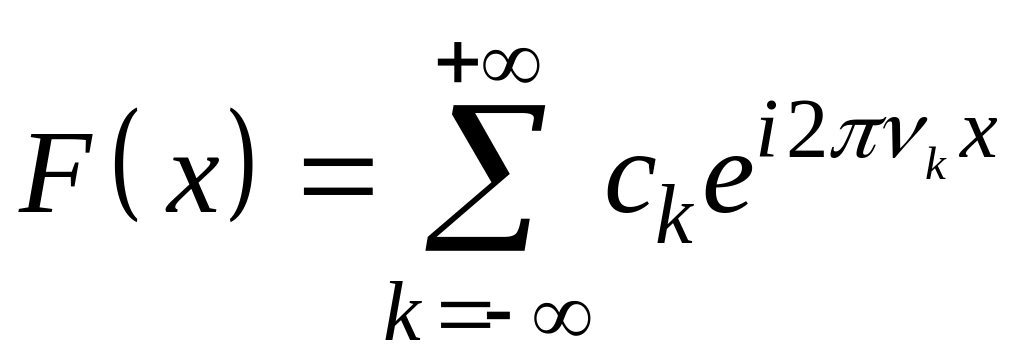 ,
где
,
где
![]() ,
,
Таким образом,
периодическая функция
может быть выражена через частотные
составляющие
![]() с частотами
с частотами
![]() ,
образующими ее спектр частот.
,
образующими ее спектр частот.
Если дана функция , то можно определить ее спектр частот.
Спектральной
функцией или спектральной плотностью
![]() ряда Фурье называется отношение
комплексной амплитуды
ряда Фурье называется отношение
комплексной амплитуды
![]() функции
периода
к приращению частоты
функции
периода
к приращению частоты
![]()
![]()
![]()
Частоты
![]() образуют бесконечную арифметическую
прогрессию с разностью
образуют бесконечную арифметическую
прогрессию с разностью
![]() .
.
Например, спектральная плотность величины, характеризующей излучение (потока излучения, силы света) - отношение рассматриваемой величины, взятой в бесконечно малом интервале, содержащем данную длину волны, к ширине этого интервала.
График зависимости
спектральной плотности от длины волны
или частоты
![]() характеризует распределение соответствующей
величины (комплексной амплитуды) по
спектру.
характеризует распределение соответствующей
величины (комплексной амплитуды) по
спектру.
А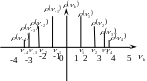 мплитудным
спектром
мплитудным
спектром
![]() называется модуль спектральной функции:
называется модуль спектральной функции:
![]()
Этот спектр
симметричен относительно оси ординат,
так как
![]() и соответственно
и соответственно
![]() =
=
![]() ,
.
,
.
Фазовым спектром
![]() называется взятый с обратным знаком
аргумент спектральной функции
называется взятый с обратным знаком
аргумент спектральной функции
![]() .
.
Так как
![]()
![]() ,
то фазовый спектр совпадает с
фазово-частотным спектром
,
то фазовый спектр совпадает с
фазово-частотным спектром
![]() ,
симметричным относительно начала
координат, только строится в зависимости
от
,
симметричным относительно начала
координат, только строится в зависимости
от
![]() :
:
Нахождение сумм числовых рядов.
Функция называется
кусочно-монотонной на отрезке![]() ,
если этот отрезок можно разбить на
конечное число отрезков:
,
если этот отрезок можно разбить на
конечное число отрезков:
![]() ,
внутри каждого из которых функция либо
строго монотонна (только возрастает
или только убывает) либо постоянна. (см.
второе условие Дирихле).
,
внутри каждого из которых функция либо
строго монотонна (только возрастает
или только убывает) либо постоянна. (см.
второе условие Дирихле).
Пусть периодическая
функция
ограничена и кусочно-монотонна на
отрезке
![]() ,
тогда в случае, если
,
тогда в случае, если
![]() интегрируема, ряд
интегрируема, ряд
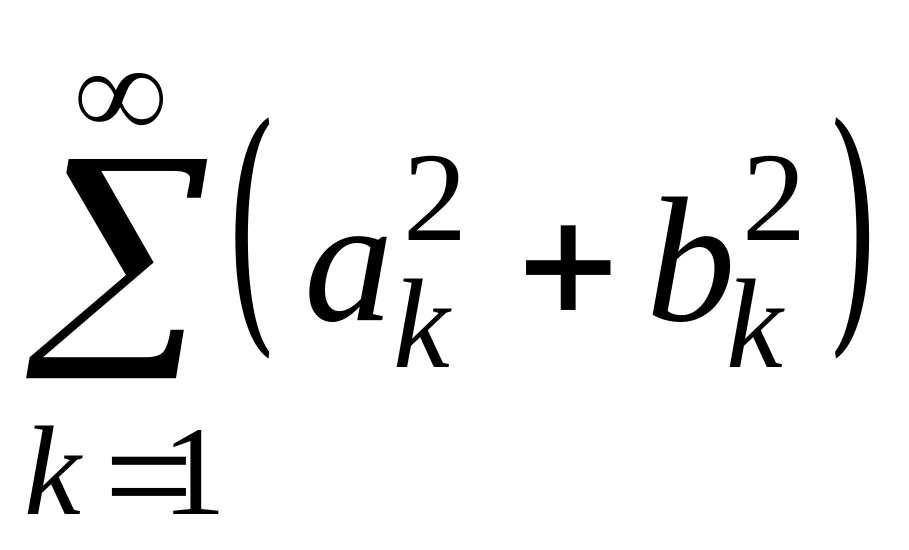 сходится и верно равенство
сходится и верно равенство
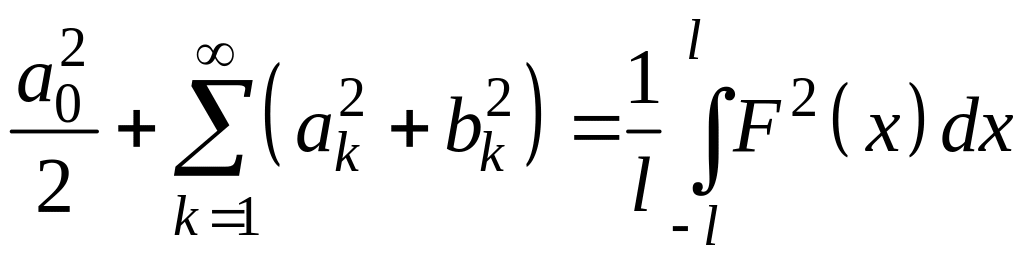 ,
где
,
где
![]()
(или
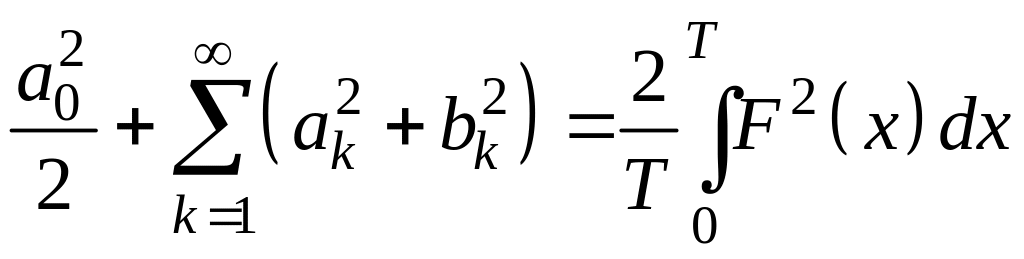 ,
учитывая периодичность
).
,
учитывая периодичность
).
Это равенство
называется равенством Парсеваля-Ляпунова.
С его помощью находится сумма ряда
,
где
![]() и
и
![]() - коэффициенты ряда Фурье.
- коэффициенты ряда Фурье.
