Ряды Фурье для четных и нечетных функций.
Функция, заданная на всей числовой оси или на интервале, симметричном относительно начала координат, называется четной, если
и
нечетной, если
.
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
Р
ассмотрим
интеграл вида
,
где
-
произвольное число из области определения
.
Если
- четная, то из геометрической интерпретации
следует:
.
Е
сли
- нечетная, то
.
Запишем ряд Фурье
для четной периодической функции
с
периодом
.
Так как
четная, то
тоже четная, а
- нечетная функция относительно
.
Тогда:
,
,
,
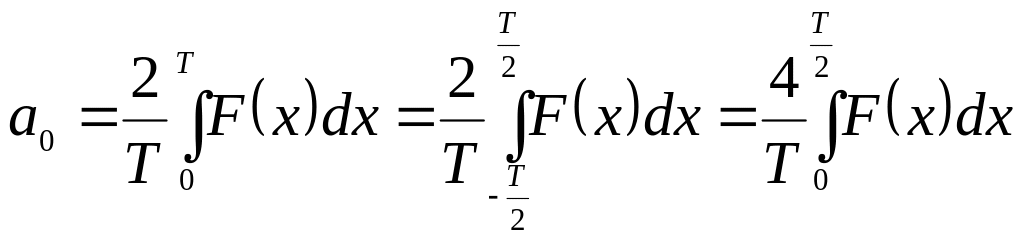и ряд Фурье имеет
вид:
.
Если нечетная периодическая функция с периодом , то нечетная, а - четная функция относительно .
Тогда
,
,
,
и ряд Фурье имеет вид:
.
Таким образом, ряд Фурье для четной функции состоит из свободного члена и косинусоидальной части. Ряд Фурье для нечетной функции состоит только из синусоидальной части.
Полученные формулы позволяют упрощать вычисления коэффициентов Фурье в случае четности или нечетности заданной функции.
Ряд Фурье в комплексной форме.
Для того, чтобы записать ряд Фурье для периодической функции в комплексной форме воспользуемся формулами Эйлера:
Тогда:
=
=
=
=
.
Пусть
=
,
=
,
и
.
Тогда
=
=
=
=
,
или
,
но при
Итак,
=
-
комплексная форма записи ряда Фурье,
где коэффициент
называется комплексной амплитудой и
определяется так:
Каждый член ряда
называется комплексным гармоническим
колебанием с частотой
(числа
называют еще волновыми числами).
Коэффициенты
называют комплексной амплитудой.
Выражения
называют гармониками. Таким образом,
разложение периодической функции
в ряд Фурье также эквивалентно
представлению ее в виде бесконечной
суммы комплексных гармонических
колебаний (комплексных гармоник).
Выведем формулы для .
При
=
=
.
При
=
=
.
При
.
Значит, для
.
Замечание(*): запись
при
означает что, например, при
=
.
Отметим, что если
- действительная функция, то
и
действительны
,
а числа
при
и
взаимно сопряжены:
: = ,
: = ,
:
и
:
.
Тогда при
,
,
,
,
,
при
,
,
,
,
.
Спектральные характеристики ряда Фурье.
Вообще, спектр - это совокупность различных значений, которые может принимать данная величина.
Спектры могут быть
непрерывными и дискретными (прерывными).
Для периодической функции спектры носят
дискретный характер, так как они
существуют только на частотах
и
и их нельзя изобразить непрерывной
кривой. Графики спектров периодических
функций имеют вид диаграмм и называются
линейчатыми.
Спектральные характеристики для вещественной формы.
Частотные спектры: представляют собой последовательность частот -ой гармоники
и частот
при
в зависимости от
:
Остальные
спектры могут быть построены относительно
обеих частот, ограничимся построением
относительно
.
Линейчатые спектры: представляют собой последовательность коэффициентов и при в зависимости от :
3. Амплитудный
спектр (амплитудно-частотный): представляет
собой последовательность амплитуд
при
в зависимости от
:
Фазовый спектр (фазово-частотный): представляет собой последовательность фаз -ой гармоники
при
в зависимости от
:
