
- •Разложение периодической функции в ряд Фурье
- •Ряды Фурье для четных и нечетных функций.
- •Ряд Фурье в комплексной форме.
- •Спектральные характеристики ряда Фурье.
- •Спектральные характеристики для вещественной формы.
- •Спектральные характеристики для комплексной формы.
- •Спектральная функция.
- •Нахождение сумм числовых рядов.
- •Разложение непериодической функции.
- •Интеграл Фурье в вещественной форме.
- •Интеграл Фурье для четной и нечетной функций.
- •Спектральные характеристики интеграла Фурье.
Разложение периодической функции в ряд Фурье
Многие явления природы происходят периодически, то есть повторяются в определенном порядке по истечении некоторого промежутка времени, называемого периодом. Математически такие явления описываются с помощью периодических функций.
Пусть
![]() - вещественная функция вещественного
аргумента. Функция
- вещественная функция вещественного
аргумента. Функция
![]() называется
периодической с периодом
называется
периодической с периодом
![]() ,
если она определена на всей вещественной
оси и для всех
,
если она определена на всей вещественной
оси и для всех
![]() выполняется равенство:
выполняется равенство:
![]() .
.
Замечание: Если
функция
имеет период
,
то она также имеет период
![]() ,
,
![]() ,
…, то есть
,
…, то есть
![]() .
.
Обычно за основной период принимают наименьшее положительное , для которого .
Следовательно,
полное представление о функции
![]() можно получить, изучив ее на любом
интервале длины
,
например:
можно получить, изучив ее на любом
интервале длины
,
например:
![]() ,
,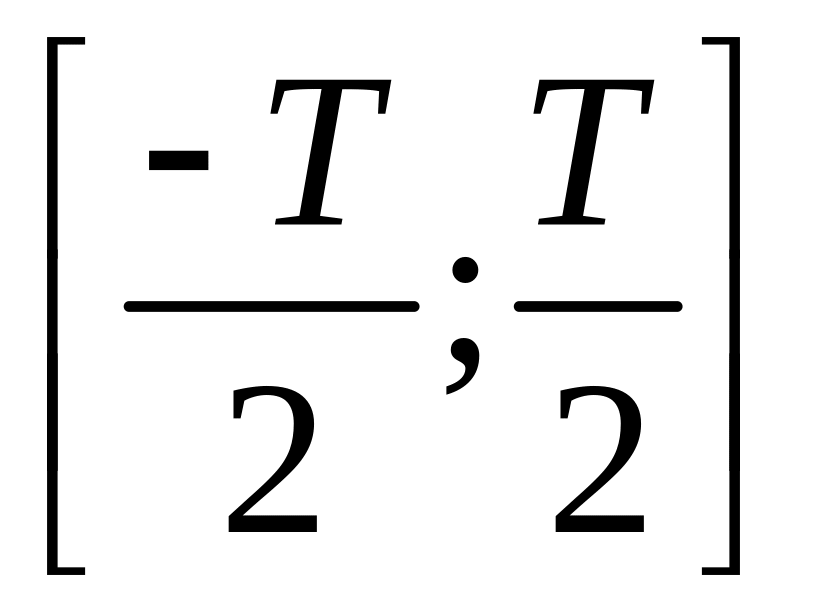 ,
,![]() ,
,![]() ,…так
как
принимает одинаковые значения при любых
,
отличающихся друг от друга на
.
,…так
как
принимает одинаковые значения при любых
,
отличающихся друг от друга на
.
Изменение функции за период называется ее колебанием.
Рассмотрим интеграл
от периодической функции
:![]() .
.
К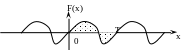 ак
известно, геометрический смысл
определенного интеграла это площадь
фигуры, ограниченной функцией
и осью
ак
известно, геометрический смысл
определенного интеграла это площадь
фигуры, ограниченной функцией
и осью
![]() на промежутке
на промежутке
![]() (см. рис.1).
(см. рис.1).
А интеграл
![]() численно равен площади заштрихованной
фигуры на рис.2
численно равен площади заштрихованной
фигуры на рис.2
В идно,
что площадь фигуры на рис.1 равна площади
фигуры на рис.2, следовательно:
идно,
что площадь фигуры на рис.1 равна площади
фигуры на рис.2, следовательно:
![]() ,
,
то есть интегралы по любым отрезкам длины от периодической функции с периодом равны.
С периодическими движениями (колебаниями) приходится иметь дело в самых различных областях знания – в теории упругости, акустике, радиотехнике, электротехнике, теории автоматического управления. В общем случае характер периодического движения может быть очень сложным.
Нужно сказать, что физики давно считали, что всякое сложное периодическое движение точки (сложное колебание) – будь то механическое колебание точки струны или электромагнитное колебание, или колебание, связанное с распространением звука – распадается на гармонические колебания, то есть сложное периодическое движение надо мыслить как сумму (конечную или бесконечную) простых гармонических колебаний того же периода, соответствующих данной частоте k (простейшими периодическими движениями являются гармонические колебания).
Физики такое разложение из реального движения получают при помощи специальных приборов – резонаторов, математики – при помощи вычислений.
Таким представлением периодической функции пользуются, например, в электротехнике: явления, происходящие в электрических цепях с несинусоидальной, периодически меняющейся электродвижущей силой, проще всего поддаются исследованию, если эту электродвижущую силу разложить на сумму гармоник.
Поэтому возникает
потребность представления периодической
функции в виде суммы более простых
периодических функций, в качестве
которых используются
![]() и
и
![]() .
.
С этой целью рассмотрим бесконечную систему тригонометрических функций:
![]() (1)
(1)
где 1=
![]() и
и
![]() ,
,
![]()
Функции
![]() и
и
![]() являются периодическими с периодом Т:
являются периодическими с периодом Т:
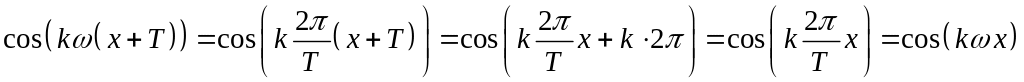 Аналогично
для
Аналогично
для
![]() .
.
Вообще минимальным
периодом для функций
![]() и
является
и
является
![]() ,
но тогда и
тоже является периодом. Постоянную
функцию (константу) можно считать
периодической любого периода.
,
но тогда и
тоже является периодом. Постоянную
функцию (константу) можно считать
периодической любого периода.
Таким образом, общий период всех функций из бесконечной системы (1) будет равен Т.
Так как функция
имеет период
,
то это означает, что одно полное колебание
происходит за промежуток времени
.
Количество
колебаний в единицу времени это
![]() ,
а за
,
а за
![]() секунд происходит
секунд происходит
![]() колебаний. Эта величина называется
круговой частотой
колебаний. Эта величина называется
круговой частотой
![]() (число колебаний за
секунд).
(число колебаний за
секунд).
Число колебаний
в секунду – величина, обратная периоду:
![]() - также называется частотой колебания,
ее единицей измерения является герц.
- также называется частотой колебания,
ее единицей измерения является герц.
![]() и
и
![]() связаны равенством
связаны равенством
![]() .
.
Введенная система тригонометрических функций является ортогональной на промежутке длины , так как интеграл по отрезку от произведения любых двух различных функций последовательности (1) равен нулю:
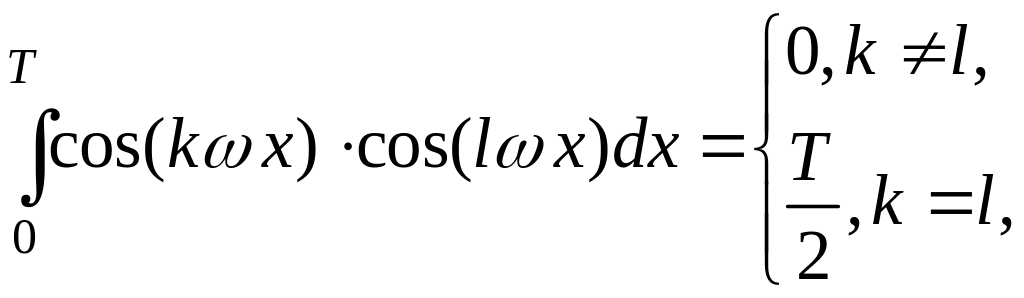

![]() ,
при
,
при
![]()
Пусть дана периодическая функция с периодом , которая необязательно является тригонометрическим многочленом. С помощью введенной системы тригонометрических функций составим тригонометрический ряд:
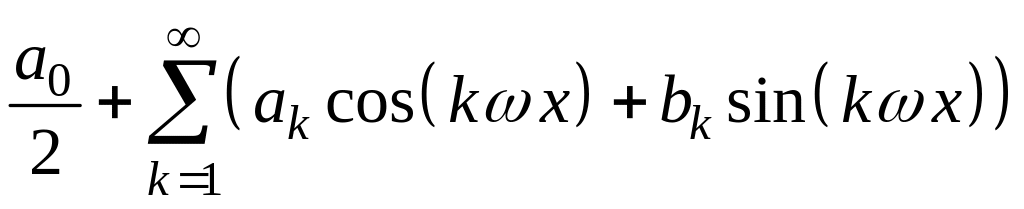 ,
(2)
,
(2)
где
![]() вычисляются по формулам:
вычисляются по формулам:
![]()
![]()
![]()
![]()
Этот ряд представляет собой частный случай функционального ряда и называется рядом Фурье для , а называются коэффициентами ряда Фурье для функции .
Слагаемое
![]() называется
называется
![]() -той
гармоникой ряда Фурье.
-той
гармоникой ряда Фурье.
Ряд Фурье сходится к функции только при определенных условиях. Эти условия называются условиями Дирихле. Сформулируем их.
Функция
удовлетворяет на отрезке
![]() условиям Дирихле, если:
условиям Дирихле, если:
непрерывна на , либо имеет на этом отрезке конечное число точек разрыва I рода.
монотонна на , либо имеет на этом отрезке конечное число экстремумов.
Теорема Дирихле: Если функция с периодом на отрезке длины удовлетворяет условиям Дирихле, то:
ряд Фурье для этой функции сходится на всей оси ,
сумма ряда Фурье равна во всех точках непрерывности этой функции:
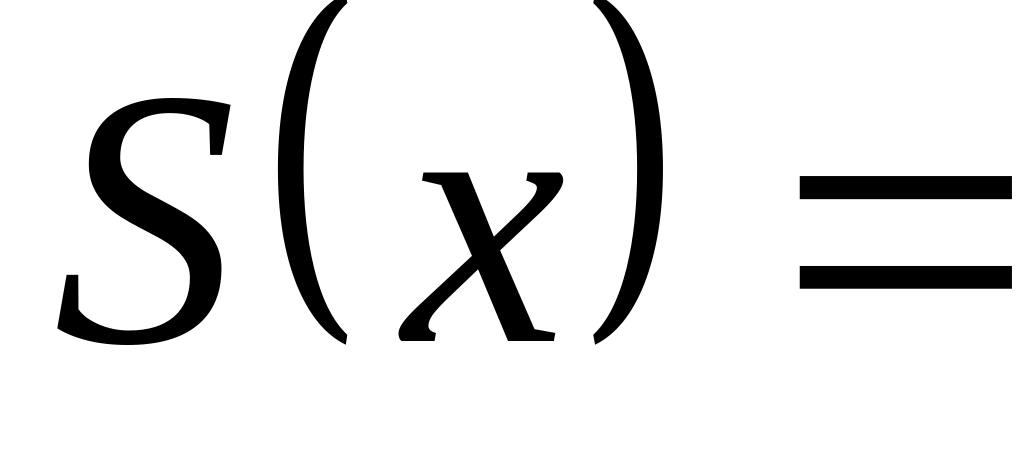 =
,
=
,
где
![]() -периодическая
функция с периодом Т.
-периодическая
функция с периодом Т.
В точках разрыва I рода функции сумма ряда равна полусумме левого и правого пределов функции в этих точках.
![]() точка
разрыва I
рода,
точка
разрыва I
рода,
![]()
В частности, если
на концах отрезка
![]() функция
терпит разрыв, то сумма ряда в этих
точках равна:
функция
терпит разрыв, то сумма ряда в этих
точках равна:
![]()
Эта теорема имеет
достаточный характер. Если на некотором
промежутке
![]() ряд Фурье сходится к функции
,
то говорят, что на этом промежутке
функция
разложена в ряд Фурье, и пишут:
ряд Фурье сходится к функции
,
то говорят, что на этом промежутке
функция
разложена в ряд Фурье, и пишут:
=
,
![]()
Пусть
на промежутке
представима функцией
![]() .
Тогда ряд Фурье для функции
совпадает с рядом Фурье для функции
,
заданной на промежутке
.
.
Тогда ряд Фурье для функции
совпадает с рядом Фурье для функции
,
заданной на промежутке
.
Ряд Фурье в виде называется рядом Фурье в вещественной форме.
Члены ряда (2)
можно записать
в виде гармоник:
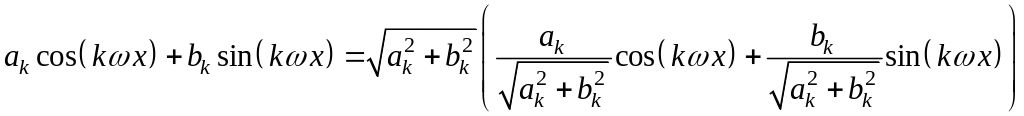
Обозначая
![]() ,
получим
,
получим
![]()
![]() ,
,
где
![]() -
-
![]() -ая
гармоника,
-ая
гармоника,
![]() - амплитуда
-ой
гармоники,
- амплитуда
-ой
гармоники,
![]() дает наибольшее отклонение точки,
движущейся по закону
дает наибольшее отклонение точки,
движущейся по закону
![]()
![]() ,
от начала координат,
,
от начала координат,
![]() - фаза k-ой
гармоники, причем, если при некотором
- фаза k-ой
гармоники, причем, если при некотором
![]() и
и
![]() ,
то при таком
гармоническое колебание не определено,
-ая
гармоника равна 0 и
,
то при таком
гармоническое колебание не определено,
-ая
гармоника равна 0 и
![]() не существует;
не существует;
![]() - частота k-ой
гармоники.
- частота k-ой
гармоники.
Тогда ряд Фурье для функции примет вид:
![]() .
.
Таким образом,
разложение периодической функции в ряд
Фурье эквивалентно представлению ее в
виде бесконечной суммы гармоник,
амплитуды которых
![]() и фазы
определяются коэффициентами Фурье
и фазы
определяются коэффициентами Фурье
![]() и
и
![]() :
:
![]() - первая гармоника,
- первая гармоника,
![]() - вторая гармоника,
- вторая гармоника,
![]() - третья гармоника,
… и так далее.
- третья гармоника,
… и так далее.
Все гармоники
имеют общий период
![]() .
.
Разложение функции в тригонометрический ряд единственно.
Аппроксимирующие тригонометрические полиномы для функции имеют вид:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
..................................
![]() .
.
Эти полиномы
представляют собой частичные суммы
ряда и являются последовательными
приближениями функции
на
![]() ,
с увеличением
они все точнее и точнее представляют
функцию
.
,
с увеличением
они все точнее и точнее представляют
функцию
.
Периодическая
функция
![]() изображает периодическое движение
(колебание) точки, имеющей в момент
времени
координату
изображает периодическое движение
(колебание) точки, имеющей в момент
времени
координату
![]() (на оси
).
(на оси
).
Функция
![]() определяет гармоническое колебание
точки с амплитудой
,
фазой
определяет гармоническое колебание
точки с амплитудой
,
фазой
![]() и частотой
и частотой
![]() .
Это функция периода
.
.
Это функция периода
.
