Развертка пирамиды

Построение развертки боковой поверхности пирамиды сводится к последовательному построению ряда треугольников (по трем их сторонам), каждый из которых равен натуральной величине соответствующей боковой грани пирамиды.

Чтобы построить развертку треугольной пирамиды (рисунок 15, необходимо определить натуральные величины ребер пирамиды любым способом. Если ребер много, то удобно воспользоваться способом прямоугольного треугольника. При этом нужно вынести построения всех треугольников в сторону от чертежа данной фигуры. Натуральные величины ребер можно найти и методом вращения вокруг горизонтально проецирующей оси i, проходящей через вершину S. На рисунке 15 показаны оба способа нахождения натуральных величин ребер пирамиды.

После того, как определим длины ребер SA, SB, SC, приступаем к построению развертки. Для этого через произвольно выбранную точку S проводим прямую l, на которой откладываем натуральную величину ребра AS. Далее строим вершину B треугольника ABS методом засечек, затем вершину С треугольника BCS и вершину А треугольника CAS. После этого достраиваем к полученной развертке боковой поверхности основание пирамиды АВС, взятое с плоскости П₁, на которую оно проецируется в натуральную величину, т.к. является горизонтальной плоскостью уровня.

На рисунке 15 показано нахождение на развертке точки К, расположенной на грани ABS.

Рисунок 15

Развертка прямого кругового цилиндра

Полная развертка прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а основание – длине окружности основания цилиндра и пристроенные к нему два круга-основания.

Для получения приближенной развертки цилиндрической поверхности заменяем последнюю на вписанную в нее 12-ти угольную правильную призму (рисунок 16).

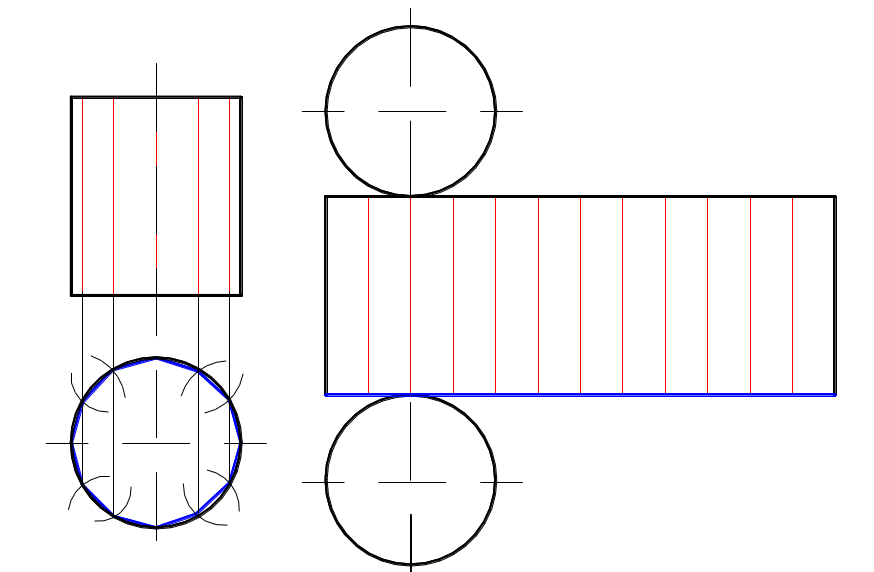
Рисунок 16

Развертка прямого кругового конуса

Полная развертка прямого кругового конуса представляет собой сектор, радиус которого равен образующей конуса, а длина дуги равна длине окружности основания конуса и пристроенный к нему круг основания.

Для получения приближенной развертки конической поверхности, усеченной фронтально проецирующей плоскостью, заменяем последнюю на вписанную в нее 12-ти угольную правильную пирамиду (рисунок 17). Для этого делим окружность основания конуса своим радиусом на 12 частей . Через эти точки деления проводим соответственно 12 образующих конуса.

Точка 1 принадлежит правой очерковой образующей конуса, проецирующейся на П₂ в натуральную величину, т.к. она является фронтальной прямой уровня, поэтому на развертке расстояние от вершины S до точки 1 равно отрезку S₂1₂. Для определения расстояний от вершины S до остальных точек пересечения образующих конуса с секущей плоскостью проводим через их фронтальные проекции прямые, параллельные фронтальной проекции основания конуса, до пересечения с одной из очерковых (правой или левой) образующих конуса. Это соответствует вращению этих образующих до положения, параллельного плоскости П₂.

Точки 10 и 11, лежащие на очерке основания конуса, находим измеряя наименьшую хорду по дуге окружности.

Рисунок 17